Погрешности в нейронных сетях

Анализ реализуемости сетей с собственными погрешностями элементов методом обратного распространения точности для оценки среднеквадратических отклонений

Все изложенные выше соображения о выполнимости метода обратного распространения точности справедливы и для метода обратного распространения точности для среднеквадратических отклонений погрешностей с учетом собственных погрешностей элементов. Отличие состоит в способе вычисления промежуточных среднеквадратических отклонений погрешностей.

Как и выше, рассмотрим участок сети, изображенный на рис. 6.9. Для этого участка нам необходимо вычислить промежуточное среднеквадратическое отклонение погрешности .

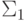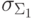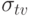Пусть собственное среднеквадратическое отклонение погрешности сумматора равно , собственное среднеквадратическое отклонение погрешности нелинейного преобразователя равно и - собственное среднеквадратическое отклонение погрешности точки ветвления.

Рассмотрим сначала вариант, когда собственные погрешности элементов добавляются к выходным сигналам этих элементов. В этом случае среднеквадратическое отклонение погрешности входного сигнала нелинейного преобразователя вычисляется по формул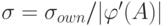е , где

- общая погрешность выходного сигнала нелинейного преобразователя. Для точки ветвления среднеквадратическое отклонение погрешности входного сигнала определяется как .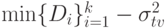

Среднеквадратическое отклонение погрешности , которое придет к входу сумматора при прямом функционировании сети, начиная от выходного сигнала сумматора 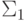( рис. 6.9), равно

Среднеквадратические отклонения погрешностей придут к каждому входу сумматора . Если сумма квадратов среднеквадратических отклонений с коэффициентами меньше квадрата среднеквадратического отклонения погрешности выходного сигнала сумматора ( ), то вычисляем разность . Оставшуюся часть квадрата среднеквадратического отклонения погрешности выходного сигнала сумматора 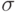распределяем равномерно по всем входам, чтобы среднеквадратические отклонения погрешностей входов превышали собственные среднеквадратические отклонения погрешностей элементов на одну и ту же величину . Тогда получаем следующую формулу

Среднеквадратические отклонения погрешностей по входам сумматора будут равны .

Пусть теперь собственные погрешности элементов добавляются к входным сигналам этих элементов. В этом случае среднеквадратическое отклонение погрешности входного сигнала нелинейного преобразователя вычисляется по формуле

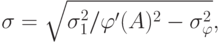
где - погрешность выходного сигнала нелинейного преобразователя. Для точки ветвления среднеквадратическое отклонение погрешности входного сигнала определяется как было указано выше.

Среднеквадратическое отклонение погрешности в этом случае равно

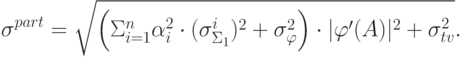
Величины 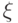для вычисления среднеквадратических отклонений погрешностей входных сигналов 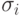вычисляются как было показано выше.

Промежуточные среднеквадратические отклонения погрешностей можно вычислять как для участков сети, так и для сети в целом.

Таким образом, мы получили формулы для вычисления среднеквадратических отклонений погрешностей сигналов нейронной сети с собственными погрешностями элементов.