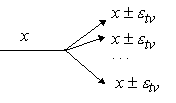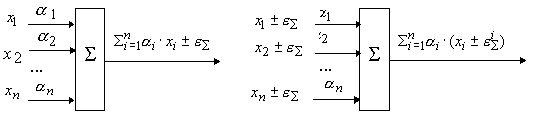Погрешности в нейронных сетях

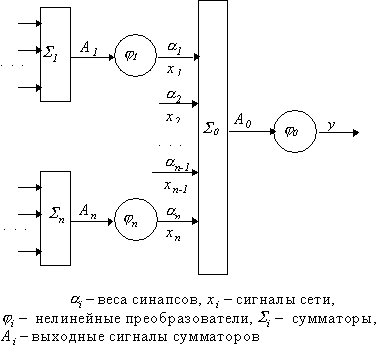
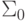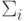Зная, как вычисляются допустимые погрешности для всех элементов стандартного нейрона, можно вычислить допустимые погрешности сигналов для всей сети. Рассмотрим участок сети, состоящий из сумматора и нелинейного преобразователя, результатом работы которого является выходной сигнал , а также из сумматоров и нелинейных преобразователей, выходные сигналы которых являются входными сигналами сумматора 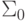(рис. 6.5). То есть мы рассматриваем два последних слоя нейронной сети, состоящие из стандартных нейронов.

Рис. 6.5.

Если заданы допустимые погрешности для выходных сигналов сети, можно вычислить допустимые погрешности для последнего слоя сети. Когда вычислены допустимые погрешности всех входных сигналов последнего слоя сети, переходим к вычислению допустимых погрешностей предпоследнего слоя и так далее. Переходя по сети в обратном направлении от слоя к слою, мы можем вычислить допустимые погрешности всех сигналов сети, в том числе допустимые погрешности входных сигналов.

Мы рассмотрели, как изменяются погрешности сигналов при прохождении через элементы сети. Предположим теперь, что не только сигналы имеют погрешности, но и все элементы сети передают приходящие к ним сигналы с некоторыми погрешностями. Пусть собственные погрешности элементов известны и фиксированы. Выясним, как влияют собственные погрешности элементов на погрешности сигналов.

Bыясним, как действуют элементы сети, имеющие собственные погрешности, при прямой работе сети.

Точка ветвления может либо вообще не иметь погрешности, либо она имеет собственную погрешность 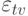. В последнем случае сигнал при прохождении через точку ветвления будет изменяться, оставаясь в интервале 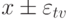( рис. 6.6).

Рис. 6.6.

Предположим, что сумматор имеет собственную погрешность 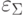. Тогда возможны следующие варианты:

1. погрешность прибавляется к выходному сигналу сумматора, т.е. при прохождении сигналов 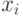через сумматор выходной сигнал сумматора будет иметь вид: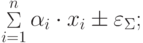
2. погрешность сумматора действует по каждому входу пропорционально ( рис. 6.7).

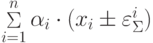Рис. 6.7.

Считаем при этом, что погрешности 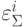равны между собой и равны , где - число входов сумматора.

Пусть собственная погрешность нелинейного преобразователя равна , - входной сигнал нелинейного преобразователя, 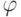- его функция активации. Собственная погрешность может добавляться или к входному сигналу : , или к выходному сигналу нелинейного преобразователя: ( рис. 6.8).

Рис. 6.8.