Погрешности в нейронных сетях
Метод обратного распространения точности для оценки среднеквадратических отклонений
Рассмотрим обученную нейросеть с вычисленными весами синапсов 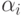 . Считаем, что погрешности входных сигналов, внутренних сигналов сети и элементов отсутствуют. При векторе входных сигналов
. Считаем, что погрешности входных сигналов, внутренних сигналов сети и элементов отсутствуют. При векторе входных сигналов 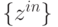 получаем вектор выходных сигналов
получаем вектор выходных сигналов  . Вектор
. Вектор  и внутренние сигналы сети
и внутренние сигналы сети 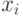 будем считать точным вектором выходных сигналов и точными сигналами сети.
будем считать точным вектором выходных сигналов и точными сигналами сети.
Рассмотрим теперь эту же сеть, но предположим, что все сигналы сети имеют некоторые погрешности. Пусть  - вектор выходных сигналов, полученный при том же векторе входных сигналов
- вектор выходных сигналов, полученный при том же векторе входных сигналов 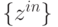 , но с погрешностями внутренних сигналов сети.
, но с погрешностями внутренних сигналов сети.
Предполагаем, что внутри каждого слоя погрешности сигналов 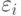 являются независимыми случайными величинами. Это предположение позволяет налагать менее жесткие требования при вычислении погрешностей сигналов.
являются независимыми случайными величинами. Это предположение позволяет налагать менее жесткие требования при вычислении погрешностей сигналов.
Пусть нам задана 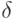 - допустимая погрешность выходных сигналов сети. То есть вектор
- допустимая погрешность выходных сигналов сети. То есть вектор  может отличаться от вектора
может отличаться от вектора  не более, чем на
не более, чем на  . Будем считать
. Будем считать 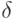 величиной среднеквадратического отклонения
величиной среднеквадратического отклонения 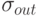 выходных сигналов сети
выходных сигналов сети  .
.
Нам нужно выяснить, каким образом могут распределяться дисперсии сигналов при заданном 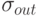 и вычислить среднеквадратические отклонения
и вычислить среднеквадратические отклонения 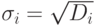 для всех сигналов сети такие, чтобы среднеквадратическое отклонение вектора выходных сигналов
для всех сигналов сети такие, чтобы среднеквадратическое отклонение вектора выходных сигналов  равнялось
равнялось 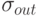 .
.
Зная среднеквадратическое отклонение выходных сигналов, можем вычислить дисперсию выходных сигналов  , а затем, переходя от элемента к элементу в обратном порядке, вычислим дисперсии
, а затем, переходя от элемента к элементу в обратном порядке, вычислим дисперсии 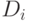 и среднеквадратические отклонения
и среднеквадратические отклонения 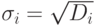 для всех сигналов сети.
для всех сигналов сети.
Типичным участком сети является стандартный нейрон. Из стандартных нейронов состоит любая нейронная сеть. Поэтому нам достаточно определить, как вычисляются среднеквадратические отклонения сигналов для элементов стандартного нейрона. Тогда мы будем иметь возможность вычислить среднеквадратические отклонения для любого участка сети.
Выясним, как вычисляются среднеквадратические отклонения для входных сигналов точки ветвления, нелинейного преобразователя и сумматора, если нам будут известны среднеквадратические отклонения выходных сигналов этих элементов.
Если дисперсии выходных сигналов точки ветвления 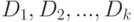 при обратном распространении не равны между собой, то в качестве дисперсии входного сигнала точки ветвления выбирается
при обратном распространении не равны между собой, то в качестве дисперсии входного сигнала точки ветвления выбирается 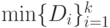 .
.
Пусть  - среднеквадратическое отклонение погрешности выходного сигнала нелинейного преобразователя. Пусть случайная величина
- среднеквадратическое отклонение погрешности выходного сигнала нелинейного преобразователя. Пусть случайная величина 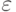 (погрешность входного сигнала нелинейного преобразователя) имеет некоторую плотность распределения
(погрешность входного сигнала нелинейного преобразователя) имеет некоторую плотность распределения 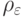 . Считаем, что математическое ожидание погрешности входного сигнала
. Считаем, что математическое ожидание погрешности входного сигнала

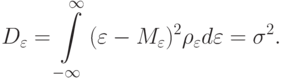
Пусть нелинейный преобразователь имеет функцию активации 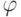 и точный входной сигнал
и точный входной сигнал  . Рассмотрим линейное приближение функции активации
. Рассмотрим линейное приближение функции активации 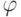 в точке
в точке  . Линейное приближение имеет вид:
. Линейное приближение имеет вид:

 .
.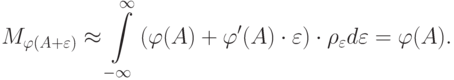
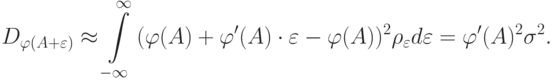
С другой стороны, нам известно, что дисперсия выходного сигнала нелинейного преобразователя равна  . Отсюда получаем
. Отсюда получаем

Таким образом, мы вычислили среднеквадратическое отклонение входного сигнала нелинейного преобразователя для любого распределения погрешности входного сигнала  .
.
Мы получили среднеквадратическое отклонение входного сигнала нелинейного преобразователя 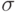 , которое одновременно является среднеквадратическим отклонением выходного сигнала сумматора с погрешностями входных сигналов
, которое одновременно является среднеквадратическим отклонением выходного сигнала сумматора с погрешностями входных сигналов

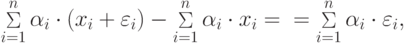
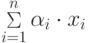 - точный выходной сигнал сумматора.
- точный выходной сигнал сумматора.Вычислим среднеквадратические отклонения 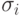 входных сигналов сумматора. Рассмотрим для этого дисперсию погрешности выходного сигнала сумматора
входных сигналов сумматора. Рассмотрим для этого дисперсию погрешности выходного сигнала сумматора
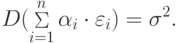
Предположим дополнительно, что 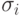 равны между собой.
равны между собой.

Получили формулу для равномерного распределения среднеквадратических отклонений 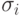 по входам сумматора. Если в качестве погрешности каждого входа рассматривать не
по входам сумматора. Если в качестве погрешности каждого входа рассматривать не 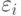 , а
, а 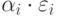 , то получим формулу для пропорционального распределения среднеквадратических отклонений
, то получим формулу для пропорционального распределения среднеквадратических отклонений 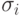 по входам сумматора.
по входам сумматора.

