Погрешности в нейронных сетях
Типы погрешностей
В методе обратного распространения точности приведены формулы для вычисления погрешностей сигналов сети. Эти формулы рассчитаны для сигналов, полученных при прямом функционировании сети с одним примером из обучающей выборки в качестве входных сигналов сети. Вообще говоря, допустимые погрешности сигналов зависят от вида входных сигналов сети. Исходя из этого, для метода обратного распространения точности можно выделить четыре типа допустимых погрешностей:
- погрешности, вычисленные для одного примера;
- погрешности, вычисленные для всей обучающей выборки;
-
погрешности, вычисленные для примеров, компоненты которых принадлежат области
 , где
, где  - размерность области,
- размерность области,  - действительные числа;
- действительные числа; -
погрешности, вычисленные для примеров, компоненты которых принадлежат области
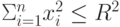 , где R - действительное число.
, где R - действительное число.
Погрешности первого типа вычисляются по формулам, описанным в методе обратного распространения точности.
Для того, чтобы вычислить погрешности второго типа, вычисляем погрешности для каждого примера из обучающей выборки. Затем в качестве допустимой погрешности для каждого элемента сети выбирается минимум допустимых погрешностей этого элемента, вычисленных для каждого примера из обучающей выборки.
Рассмотрим, как вычисляются допустимые погрешности третьего и четвертого типов. В формулах для вычисления допустимых погрешностей входной сигнал используется только у нелинейного преобразователя. Допустимые погрешности остальных элементов сети от входных сигналов не зависят. Поэтому для вычисления этих типов погрешностей следует выяснить, какие сигналы будут входными для нелинейных преобразователей, если входные сигналы сети принадлежат области, которая является прямоугольником или шаром.
Для начала рассмотрим допустимые погрешности третьего типа, то есть те допустимые погрешности элементов сети, которые получаются при входных сигналах, принадлежащих прямоугольной области. Нам известны интервалы, в которых изменяются входные сигналы сети. Требуется вычислить интервалы для входных сигналов каждого элемента сети. Будем вычислять их следующим образом. При прохождении интервалов через сумматор концы интервалов соответствующих входов умножаются на веса синапсов  и затем складываются. Предположим, что функция активации нелинейного преобразователя непрерывна и монотонна. Тогда в качестве концов интервала его выходного сигнала берутся значения характеристической функции нелинейного преобразователя от концов интервала входного сигнала. Точка ветвления посылает приходящий к ней интервал на входы следующих элементов. Таким образом, для каждого элемента сети мы можем вычислить интервал,
в котором изменяются его входные сигналы. Нас интересуют интервалы, в которых изменяются входные сигналы нелинейных преобразователей. Для того, чтобы вычислить допустимые погрешности входного сигнала нелинейного преобразователя, необходимо вычислить максимум производной функции активации нелинейного преобразователя на интервале изменения его входных сигналов и затем разделить на эту величину допустимую погрешность выходного сигнала нелинейного преобразователя.
и затем складываются. Предположим, что функция активации нелинейного преобразователя непрерывна и монотонна. Тогда в качестве концов интервала его выходного сигнала берутся значения характеристической функции нелинейного преобразователя от концов интервала входного сигнала. Точка ветвления посылает приходящий к ней интервал на входы следующих элементов. Таким образом, для каждого элемента сети мы можем вычислить интервал,
в котором изменяются его входные сигналы. Нас интересуют интервалы, в которых изменяются входные сигналы нелинейных преобразователей. Для того, чтобы вычислить допустимые погрешности входного сигнала нелинейного преобразователя, необходимо вычислить максимум производной функции активации нелинейного преобразователя на интервале изменения его входных сигналов и затем разделить на эту величину допустимую погрешность выходного сигнала нелинейного преобразователя.
Таким образом вычисляются допустимые погрешности сигналов сети для прямоугольной области входных сигналов сети.
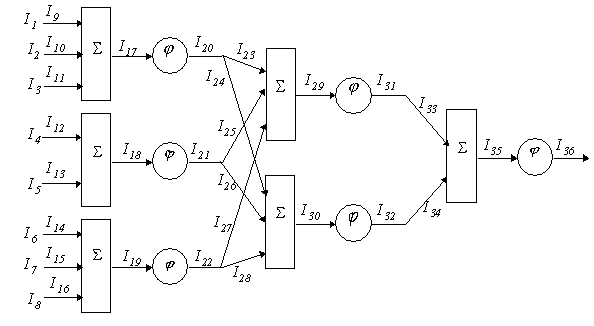
Рассмотрим пример, в котором будем вычислять погрешности третьего типа. Воспользуемся нейросетью, изображенной на рис. 6.9. Нейросеть имеет такие же веса синапсов, но входные сигналы принадлежат прямоугольной области:
![I_1 {\rm{ = [ - 2}}{\rm{,6]; }}I_2 {\rm{ = [3}}{\rm{,11]; }}I_3 {\rm{ = [1}}{\rm{.5}}{\rm{,4]; }}I_4 {\rm{ = [2}}{\rm{,7]; }}I_5 {\rm{ = [4}}{\rm{,10]; }}I_6 {\rm{ = [ - 5}}{\rm{,5]; }}\\ I_7 {\rm{ = [1}}{\rm{,8]; }}I_8 {\rm{ = [ - 4}}{\rm{,6]}}{\rm{.}}](/sites/default/files/tex_cache/7578be9a854a637685842294240d04ef.png)
Сигналы сети изменяются в следующих интервалах:
![\begin{array}{l}
I_9 {\rm{ = [ - 0}}{\rm{.6}}{\rm{,3}}{\rm{.6]; }}I_{10}{\rm{ = [2}}{\rm{.85}}{\rm{,10}}{\rm{.45]; }}I_{11}{\rm{ = [0}}{\rm{.96}}{\rm{,2}}{\rm{.56]; }}I_{12}{\rm{ = [0}}{\rm{.56}}{\rm{,1}}{\rm{.96];}}\\
I_{13}{\rm{ = [3}}{\rm{,7}}{\rm{.5]; }}I_{14}{\rm{ = [ - 2}}{\rm{.7}}{\rm{,2}}{\rm{.7]; }}I_{15}{\rm{ = [0}}{\rm{.41}}{\rm{,3}}{\rm{.28]; }}I_{16}{\rm{ = [ - 1}}{\rm{.12}}{\rm{,1}}{\rm{.68]; }}\\
I_{17}{\rm{ = [3}}{\rm{.21}}{\rm{,16}}{\rm{.61]; }}I_{18}{\rm{ = [3}}{\rm{.56}}{\rm{,9}}{\rm{.46]; }}I_{19}{\rm{ = [ - 3}}{\rm{.41}}{\rm{,7}}{\rm{.66]; }}I_{20}{\rm{ = [0}}{\rm{.62}}{\rm{,0}}{\rm{.89];}}\\
I_{21}{\rm{ = [0}}{\rm{.64}}{\rm{,0}}{\rm{.83]; }}I_{22}{\rm{ = [ - 0}}{\rm{.63}}{\rm{,0}}{\rm{.79]; }}I_{23}{\rm{ = [0}}{\rm{.07}}{\rm{,0}}{\rm{.1]; }}I_{24}{\rm{ = [0}}{\rm{.45}}{\rm{,0}}{\rm{.65];}}\\
I_{25}{\rm{ = [0}}{\rm{.39}}{\rm{,0}}{\rm{.51]; }}I_{26}{\rm{ = [0}}{\rm{.34}}{\rm{,0}}{\rm{.44; }}I_{27}{\rm{ = [ - 0}}{\rm{.2}}{\rm{,0}}{\rm{.26]; }}I_{28}{\rm{ = [ - 0}}{\rm{.55}}{\rm{,0}}{\rm{.69];}}\\
I_{29}{\rm{ = [0}}{\rm{.26}}{\rm{,0}}{\rm{.86]; }}I_3 {\rm{ = [0}}{\rm{.24}}{\rm{,1}}{\rm{.78]; }}I_{31}{\rm{ = [0}}{\rm{.12}}{\rm{,0}}{\rm{.3]; }}I_{32}{\rm{ = [0}}{\rm{.1}}{\rm{,0}}{\rm{.47];}}\\
I_{33}{\rm{ = [0}}{\rm{.04}}{\rm{,0}}{\rm{.1]; }}I_{34}{\rm{ = [0}}{\rm{.07}}{\rm{,0}}{\rm{.32]; }}I_{35}{\rm{ = [0}}{\rm{.11}}{\rm{,0}}{\rm{.42]; }}I_{36}{\rm{ = [0}}{\rm{.05}}{\rm{,0}}{\rm{.17]}}{\rm{.}}\\
\end{array}](/sites/default/files/tex_cache/11192d41f4abe274591ab23e91526179.png)
Мы можем вычислить максимум производной функции активации на интервале изменения входного сигнала нелинейного преобразователя.
![\max \varphi '_{[3.21,16.61]} = 0.07;](/sites/default/files/tex_cache/24a78041015ade274c16d50f838e0a97.png)
![\max \varphi '_{[3.56,9.46]} = 0.06;](/sites/default/files/tex_cache/85129c244a42bee43f259e9bf43df375.png)
![\max \varphi '_{[ - 3.41,7.66]} = 0.07;](/sites/default/files/tex_cache/242081dcd3f7011b2de0b7465dc00fc1.png)
![\max \varphi '_{[0..26,0.86]} = 0.39;](/sites/default/files/tex_cache/d74b95ac210e37bf807794a292767176.png)
![\max \varphi '_{[0..24,1.78]} = 0.4;](/sites/default/files/tex_cache/0b9c84f3c603afa67c3c440bc08302e9.png)
![\max \varphi '_{[0.11,0.42]} = 0.45](/sites/default/files/tex_cache/a4d3e5bcf432354d1a083eea1454711c.png) .
.Зная эти величины, можно вычислить допустимые погрешности третьего типа.
Выясним теперь, как вычисляются допустимые погрешности сигналов четвертого типа, то есть погрешности, получающиеся, когда область входных сигналов сети является шаром.
Рассуждения, приведенные выше для допустимых погрешностей третьего типа, справедливы и для допустимых погрешностей четвертого типа. Отличие состоит в том, что нам необходимо "развернуть" шаровую область таким образом, чтобы получить интервалы, в которых изменяются входные сигналы элементов.
Рассмотрим для этого квадраты выходных сигналов сумматоров входного слоя сети. Используя неравенство Коши, получаем

где  - число входных сигналов сумматора. Получили интервалы, в которых изменяются выходные сигналы сумматоров входного слоя нейронной сети. Используя эти интервалы, можем вычислить интервалы, в которых изменяются входные сигналы элементов сети. Затем, как уже было описано выше, вычисляем допустимые погрешности входных сигналов нелинейных преобразователей.
- число входных сигналов сумматора. Получили интервалы, в которых изменяются выходные сигналы сумматоров входного слоя нейронной сети. Используя эти интервалы, можем вычислить интервалы, в которых изменяются входные сигналы элементов сети. Затем, как уже было описано выше, вычисляем допустимые погрешности входных сигналов нелинейных преобразователей.
Обсуждение
Как метод обратного распространения точности, так и метод обратного распространения среднеквадратических отклонений погрешностей можно применять к сетям не только слоистой структуры, но также к циклическим и полносвязным сетям. Рассматривая такт функционирования сети как слой, "разворачиваем" циклические и полносвязные сети в сети слоистой структуры. Вычисляем допустимые погрешности (среднеквадратические отклонения погрешностей) для сигналов стандартных нейронов каждого слоя. Затем "сворачиваем" слоистую сеть в исходную. Так как каждый слой полученной сети на самом деле является тактом функционирования, то для каждого сигнала сети на разных тактах получаем разные допустимые погрешности (среднеквадратические отклонения погрешностей). В качестве допустимой погрешности (среднеквадратического отклонения погрешности) для каждого сигнала сети выбирается минимум этих величин по всем тактам.
Идея этих методов возникла при решении задачи бинаризации нейронной сети. Бинаризация состоит в построении такой сети, которая функционирует так же, как и исходная, но имеет веса синапсов, равные 0 или 1 (вариант: +1 или -1 ).
Но метод обратного распространения точности и метод обратного распространения среднеквадратических отклонений погрешностей сигналов сети интересен не только и не столько в приложении к задаче бинаризации. Их можно применять при решении ряда других задач. Например, вычислив допустимые погрешности (среднеквадратические отклонения погрешностей) для всей сети, можно выяснить, в каких пределах можно варьировать входные данные и сигналы на любом участке сети, чтобы вектор выходных сигналов при этом изменился не более, чем на заданную величину.
Метод обратного распространения точности для среднеквадратических оценок погрешности позволяет получать формулы для вычисления погрешностей сигналов сети, налагающие менее жесткие ограничения на величину погрешностей по сравнению с гарантированными интервальными оценками погрешностями. Если для гарантированных интервальных оценок при обратном прохождении слоев допустимые погрешности сигналов уменьшаются, то для среднеквадратических оценок погрешностей есть ситуации, когда погрешности увеличиваются от последнего слоя к первому. Если погрешности сигналов являются независимыми случайными величинами, то, как показано в примере, даже при больших погрешностях входных сигналов получаются достаточно точные выходные сигналы.
Заключение.
Таким образом, решение задачи вычисления допустимых погрешностей (среднеквадратических отклонений погрешностей) для каждого сигнала сети методом обратного распространения точности удивительно похоже на метод обратного распространения ошибки, но с другими правилами прохождения элементов. Метод позволяет формулировать требования к точности вычисления и реализации технических устройств, если известны требования к точности выходных сигналов сети.