Погрешности в нейронных сетях
Мы выяснили как вычисляются допустимые погрешности сигналов сети. При этом мы не выделяли особо тот вклад, который вносят в погрешность сигнала сами элементы. Рассмотрим теперь, как вычисляются допустимые погрешности сигналов сети при обратном распространении точности с учетом собственных погрешностей элементов стандартного нейрона.
Начнем вычисление допустимых погрешностей сигналов сети с учетом собственных погрешностей элементов с точки ветвления. Пусть точка ветвления имеет собственную погрешность 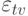 . Предположим, что допустимые погрешности выходных сигналов точки ветвления равны
. Предположим, что допустимые погрешности выходных сигналов точки ветвления равны 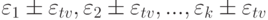 . Для увеличения точности вычислений необходимо накладывать на допустимые погрешности наиболее жесткие требования. Поэтому в качестве допустимой погрешности входного сигнала точки ветвления при обратном распространении следует выбирать погрешность
. Для увеличения точности вычислений необходимо накладывать на допустимые погрешности наиболее жесткие требования. Поэтому в качестве допустимой погрешности входного сигнала точки ветвления при обратном распространении следует выбирать погрешность  .
.
Следующий элемент стандартного нейрона - нелинейный преобразователь. Если нелинейный преобразователь имеет собственную погрешность  , которая добавляется к его выходному сигналу, и погрешность его выходного сигнала равняется
, которая добавляется к его выходному сигналу, и погрешность его выходного сигнала равняется 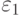 , то допустимая погрешность входного сигнала нелинейного преобразователя равняется
, то допустимая погрешность входного сигнала нелинейного преобразователя равняется 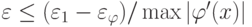 , где
, где
![x \in \left[ {\varphi^{- 1}(y - \varepsilon_1 + \varepsilon_\varphi ), \varphi^{- 1}(y + \varepsilon_1 - \varepsilon_\varphi )}\right]](/sites/default/files/tex_cache/e7b88829a3a900707bd06a6e7a147dcc.png)
 .
.Предположим теперь, что собственная погрешность нелинейного преобразователя  добавляется к его входному сигналу
добавляется к его входному сигналу  , и при обратном распространении точности погрешность выходного сигнала нелинейного преобразователя равняется
, и при обратном распространении точности погрешность выходного сигнала нелинейного преобразователя равняется 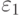 . Рассмотрим наихудший вариант, когда входной сигнал нелинейного преобразователя находится в интервале
. Рассмотрим наихудший вариант, когда входной сигнал нелинейного преобразователя находится в интервале
![\left[ {x - \varepsilon - \varepsilon_\varphi ,x + \varepsilon + \varepsilon_\varphi }\right].](/sites/default/files/tex_cache/44826f6ecacb198103d7415abf1d7466.png)
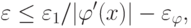
![x \in \left[ {\varphi^{- 1}(y - \varepsilon_1 ) - \varepsilon_\varphi ,\varphi^{- 1}(y + \varepsilon_1 ) + \varepsilon_\varphi }\right]](/sites/default/files/tex_cache/38fe9b8f1c943119aa1ed852c84ce61d.png) .
.Рассмотрим допустимую погрешность в линейном приближении:
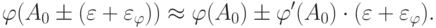

Получаем:


И, наконец, перейдем к вычислению допустимых погрешностей входных сигналов сумматора. Рассмотрим вариант, при котором собственная погрешность сумматора 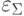 добавляется к его выходному сигналу, и допустимая погрешность выходного сигнала сумматора равняется
добавляется к его выходному сигналу, и допустимая погрешность выходного сигнала сумматора равняется  . При обратном распространении точности получаем, что равномерно, пропорционально и приоритетно по выше полученным формулам распределяется погрешность
. При обратном распространении точности получаем, что равномерно, пропорционально и приоритетно по выше полученным формулам распределяется погрешность  .
.
Если же собственная погрешность сумматора пропорционально распределяется по его входам, и допустимая погрешность выходного сигнала сумматора равняется 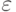 , то допустимые погрешности для входов сумматора вычисляются следующим образом. Пусть
, то допустимые погрешности для входов сумматора вычисляются следующим образом. Пусть  - выходной сигнал сумматора без погрешностей. Тогда
- выходной сигнал сумматора без погрешностей. Тогда  - выходные сигналы сумматора с учетом собственных погрешностей сумматора
- выходные сигналы сумматора с учетом собственных погрешностей сумматора 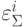 и погрешностей входных сигналов
и погрешностей входных сигналов 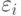 :
:
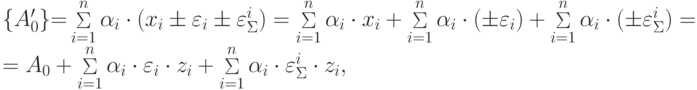
где 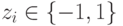 . Для того, чтобы все множество
. Для того, чтобы все множество  попало в интервал
попало в интервал
![[A_0 - \varepsilon ,A_0 + \varepsilon ]](/sites/default/files/tex_cache/5f8ad3c68eb4cd99fe0d41ac6d602e8e.png)

где максимум берется по всем 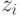 . Из этого неравенства, предполагая что
. Из этого неравенства, предполагая что 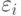 равны между собой, получаем требуемую оценку для
равны между собой, получаем требуемую оценку для 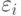 :
:
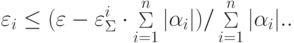
Мы получили формулы для вычисления допустимых погрешностей сигналов для любого участка сети с учетом того, что все элементы имеют собственные погрешности, которые вносят свой вклад в погрешность выходного сигнала этих элементов.
