|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Лабораторная работа № 5: Использование фиктивных переменных для моделирования структурных изменений
По имеющимся данным определить наличие структурных изменений. Построить модель, использующую фиктивную переменную, которая отражала бы имеющиеся структурные изменения.
Варианты заданий представлены в табл. 1.
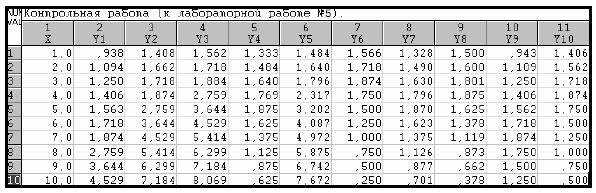
Таблица 1
Отчет по лабораторной работе № 5
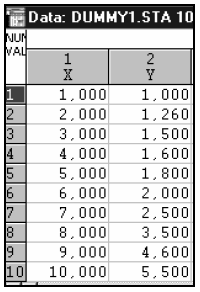
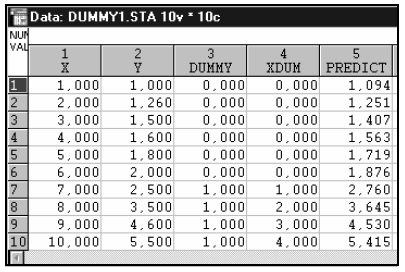
Пусть имеются следующие данные (табл. 2).
Таблица 2
Построенное парное уравнение регрессии будет иметь вид

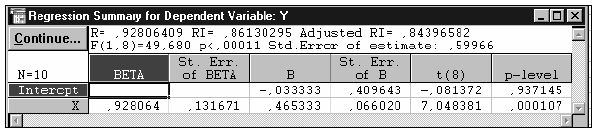
Результаты расчетов значимости коэффициентов регрессии представлены в табл. 3.
Таблица 3
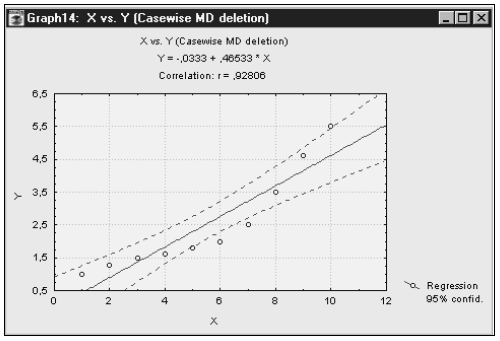
Построим доверительный интервал для уравнения регрессии (рис. 1).
Исследование остатков показывает, что существует систематическое смещение в их распределении, а график остатков свидетельствует о нарушении независимости случайной составляющей  от величины объясняющей переменной
от величины объясняющей переменной  (рис. 2).
(рис. 2).
Вместе с тем следует отметить выполнение нормальности распределения остатков (рис. 3).
Для устранения отмеченных нарушений условий Гаусса - Маркова вводится фиктивная переменная по следующему правилу:
Уравнение регрессии зададим в виде

Для построения уравнения регрессии выполним следующие преобразования (табл. 4):
Таблица 4
Оценка параметров уравнения регрессии приведена в табл. 5.
Таблица 5
Полученное уравнение регрессии будет иметь вид
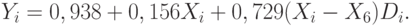
Представим это уравнение в следующем виде:
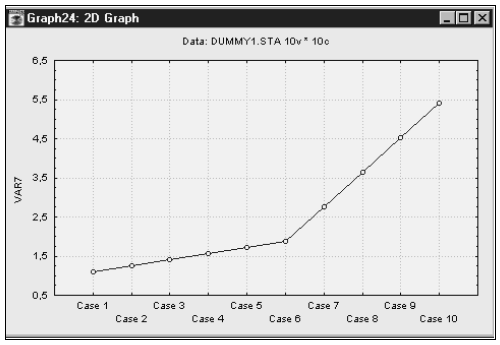
Непрерывность графика уравнения регрессии хорошо будет видна, если зависимость между переменными представить графически (рис. 4).