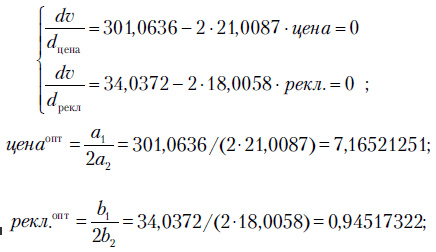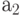Лабораторная работа № 2: Модель множественной линейной регрессии

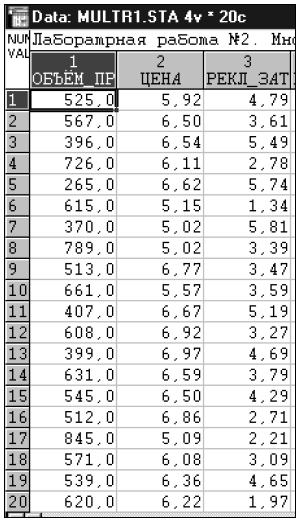
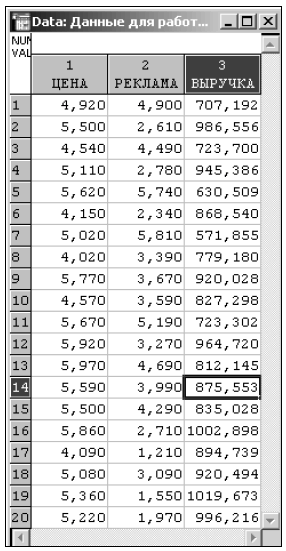
Предприятие ведет продажу однородной сельскохозяйственной продукции. Руководство предприятия проводит изучение зависимости объема продаж от выбранной цены. При этом оно проводит рекламную акцию и несет некоторые расходы на рекламу. Данные наблюдений приведены в табл. 1, где - объем продаж (кг); - цена одной единицы продукции (руб.), - расходы на рекламу (100 руб.).

Таблица 1

Требуется:

1. найти зависимость объема () продаж от цены () и рекламных расходов ();
2. экономически обосновать знаки коэффициентов в построенных моделях;
3. рассмотреть модель, учитывающую, что для расходов на рекламу существует эффект насыщения, т.е. начиная с некоторого момента вложения в рекламу перестают приводить к увеличению объема продаж. Рассмотреть зависимость вида ;
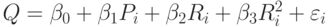4. найти МНК-оценки коэффициентов множественной регрессии. Оценить значимость полученного уравнения в целом и значимость отдельных коэффициентов;
5. оценить прогностические возможности полученного регрессионного уравнения, учитывая коэффициент детерминации;
6. найти 95%-ные доверительные интервалы коэффициентов ;
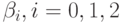7. дать экономическую интерпретацию коэффициентов множественной регрессии;
8. найти объем продаж при цене единицы продукции 6 руб. и рекламных расходах 280 руб. Вычислить 95%-ный доверительный интервал для величины объема продаж.

Отчет по лабораторной работе № 2

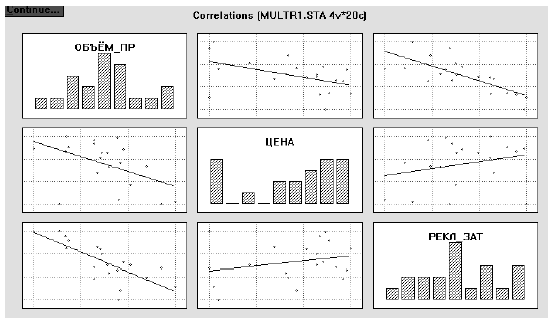
I. Определим наличие статистической зависимости между переменными. Для этого вычислим корреляционную матрицу (табл. 2) и описательные статистики (табл. 3), построим поля рассеяния и гистограммы исходных признаков (рис. 1).

Таблица 2

Таблица 3

Рис. 1.

Значимые коэффициенты корреляции свидетельствуют о том, что имеется статистическая связь между объемом продаж и ценой единицы продукции , а также между объемом продаж и расходами на рекламу . Причем связь между объемом продаж и ценой единицы продукции отрицательная, а значит, с увеличением цены объем продаж уменьшается. Этот вывод не противоречит основным представлениям экономической теории и здравому смыслу.

Иначе обстоит дело с расходами на рекламу и объемом продаж. Значимая отрицательная корреляционная связь показывает, что с увеличением расходов на рекламу объемы продаж продукции падают. Это может свидетельствовать или об отрицательном эффекте рекламной акции (например, в результате неграмотной ее организации), или о том, что связь между рассматриваемыми переменными не является прямой, т.е. реклама влияет на результирующий признак опосредованно, через некоторые другие переменные.

Регрессионная модель зависимости объема продаж от затрат на рекламу представлена в табл. 4.

Таблица 4

Для более подробного исследования рассмотрим уравнение парной регрессии

ОБЪЕМ_ПР = 877,0006 – 84,8295 РЕКЛ_ЗАТ, 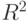= 0,56383892.

Все коэффициенты уравнения регрессии значимы на стандартном 5%-ном уровне.

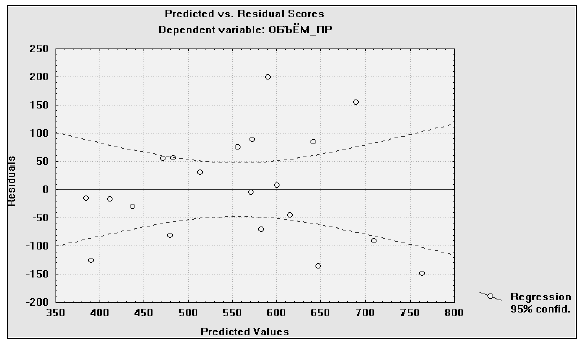
Анализ остатков построенного уравнения регрессии показывает, что более половины наблюдаемых значений находятся за пределами 95%-ного доверительного коридора (трубки) (рис. 2). Это указывает на то, что, несмотря на значимость полученного уравнения, оно может быть улучшено за счет введения в него дополнительных объясняющих переменных.

Рис. 2.

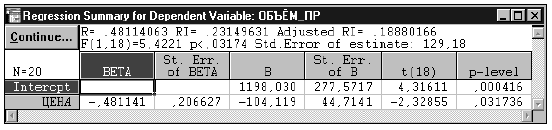
Регрессионная модель зависимости объема продаж от цены товара представлена в табл. 5.

Таблица 5

Уравнение регрессионной зависимости между объемом продаж и ценой

ОБЪЕМ_ПР = 1198,030 - 104,119 ЦЕНА, 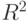= 0,23149631

хотя и является значимым ( - значение менее 0,0317), все же недостаточно хорошо воспроизводит качество зависимости ().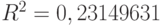

Проведенный предварительный анализ свидетельствует о необходимости использования более сложной модели, в частности, модели, позволяющей одновременно учитывать влияние всей совокупности факторов.

Регрессионная модель зависимости объема продаж от затрат на рекламу и цену товара представлена в табл. 6.

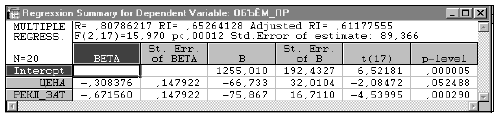
Таблица 6

Уравнение множественной регрессии, одновременно учитывающее оба фактора - и , имеет вид

ОБЪЕМ_ПР = 1255,010 - 66,733 ЦЕНА - 75,867 РЕКЛ_ЗАТ, 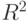= 0,65264.

Это уравнение значимо (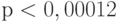) и на 65,26% объясняет вариацию зависимой переменной. Однако в этом уравнении знак перед переменной РЕКЛ_ЗАТ не соответствует ожиданиям: естественно было предположить, что увеличение рекламных расходов будет приводить к увеличению объема продаж, т.е. знак перед переменной РЕКЛ_ЗАТ должен быть положительным.

В использовании рекламы существенным является "эффект насыщения", заключающийся в том, что при увеличивающемся уровне расходов каждый последующий рубль дает меньшую отдачу, чем при начальном уровне расходов. С учетом этого в модель вводится переменная КВ_РЕКЛ, численно равная квадрату рекламных затрат. (Как известно, квадратичная функция 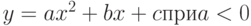обладает локальным максимумом.) Предполагается, что новая переменная будет иметь в регрессионной модели отрицательный знак, если сделанные предположения имеют место.

Результаты расчета коэффициентов уравнения регрессии подтверждают справедливость сделанных предположений:

R2 = 0,83357.

Множественная регрессионная модель представлена в табл. 7.

Таблица 7

Полученное уравнение регрессии является значимым и примерно на 87,4% (поскольку коэффициент множественной детерминации 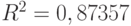) объясняет вариацию зависимой переменной. Все входящие в уравнение переменные значимы на уровне менее 1%.

Дисперсионный анализ уравнения регрессии представлен в табл. 8.

Доверительные интервалы для коэффициентов уравнения регрессии определяются с учетом того, что число степеней свободы модели равняется 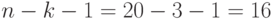, где - число наблюдений, - число объясняющих переменных модели, а 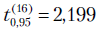. Значения ошибок (точнее, средних квадратичных отклонений) коэффициентов следует взять из таблицы результатов регрессионного анализа. Используя формулу

получим .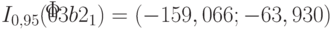

Гипотезу о несущественном влиянии переменной (цены) на зависимую переменную (объем продаж) отвергаем, так как .

Аналогичные выводы можно сделать относительно других переменных, анализируя построенные доверительные интервалы. Так, 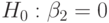отвергаем, поскольку 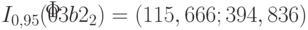. К такому же выводу о значимости коэффициента 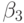можно прийти на основании рассмотрения соответствующего доверительного интервала .

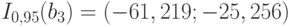Экономическая интерпретация коэффициентов уравнения регрессии связана с анализом рассматриваемой ситуации. Так, значение коэффициента при переменной (цена), равное -111,498, указывает на то, что в случае увеличения цены на одну единицу при прочих равных условиях объем продаж в среднем сократится на 111 кг. Более надежным (практически достоверным, имеющим вероятность 0,95) будет утверждение о том, что уменьшение объема продаж будет находиться в интервале от 63 до 159 кг.

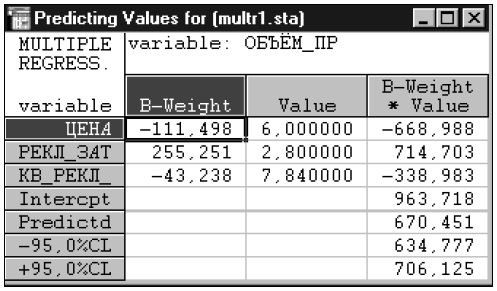
Для вычисления объема продаж при цене единицы продукции 6 руб. и рекламных расходах 280 руб. следует воспользоваться режимом Predict dependent var. Результаты расчетов представлены в табл. 9.

Таблица 9

Анализ этих результатов показывает, что при указанных выше значениях объясняющих переменных объем продаж составит в среднем 670 кг. При этом с вероятностью 0,95, т.е. практически достоверно, можно ожидать, что среднее значение величины Q будет находиться в интервале от 634 до 706 кг.

II. Теперь представим упрощенный вариант отчета по лабораторной работе № 2, но содержащий описание процедуры оптимизации продажной цены с целью максимизации выручки.

Для этого воспользуемся исходными данными, представленными в табл. 10.

Выберем в качестве зависимой переменной выручку (объем продаж), а в качестве предсказывающих независимых факторов - цену продукта и расходов на рекламу. Сначала построим линейную модель, результаты расчетов представлены в табл. 11.

Таблица 10

Таблица 11

Несмотря на то что линейное уравнение значимо (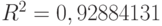), значимыми оказались и коэффициенты уравнения, т.е. по эконометрическим признакам уравнение можно признать хорошим. Однако оно не согласуется с экономическим смыслом поставленной задачи. Некоторые коэффициенты оказались отрицательными, а значит, увеличение расходов на рекламу влечет уменьшение объемов продаж. На практике такое уменьшение происходит, только если цена превысит свой оптимальный уровень, а расходы на рекламу выйдут за разумный предел. Поэтому требуется усложнить модель - включить в нее квадратичные слагаемые. Добавив квадратичные слагаемые в табл. 10, получим табл. 12.

Таблица 12

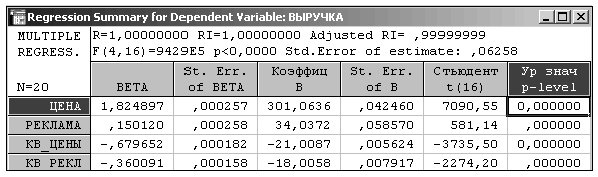
Результаты расчетов по квадратичной модели представим в табл. 13.

Таблица 13

Полученная регрессия отражает экономический смысл связей между объемом продаж, ценой продукта и расходами на рекламу. При малых значениях цены и расходов на рекламу их положительные коэффициенты определяют движение выручки. Следовательно, выручка будет расти. Если цена и расходы превысят оптимальный уровень, то определяющими движение выручки станут отрицательные коэффициенты при квадрате цены и квадрате расходов на рекламу. В этом случае выручка будет падать. В полученной регрессии есть один существенный недостаток. Если предположить, что цена продукта нулевая и расходы на рекламу нулевые, то выручка должна быть равна нулю. В нашей модели это не так, поскольку остается свободный член не равный нулю. Следовательно, нужно построить регрессию с квадратичными слагаемыми и с нулевым свободным членом (табл. 14).

Таблица 14

Окончательная модель объема продаж выглядит следующим образом:

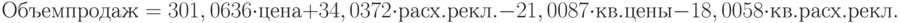
Рассчитаем оптимальные значения цены и расходы на рекламу исходя из полученной модели и условия максимизации выручки:

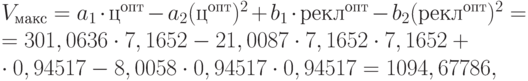
где

	-	коэффициент при цене;
	-	коэффициент при цене в квадрате;
	-	коэффициент при расходах на рекламу;
	-	коэффициент при расходах на рекламу в квадрате;
	-	объем продаж.