Представление множеств. Деревья. Сбалансированные деревья.
14.1. Представление множеств с помощью деревьев
Полное двоичное дерево. T-деревья
Нарисуем точку. Из нее проведем две стрелки (влево вверх ивправо
вверх) в две другие точки. Из каждой из этих точек проведем
по две стрелки итак далее. Полученную картинку
(в  -ом слое будет
-ом слое будет 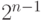 точек) называют полным
двоичным деревом.
Нижнюю точку называют корнем. У каждой вершины есть
два сына (две вершины, в которые идут стрелки) -
левый и правый. У всякой вершины, кроме
корня, есть единственный отец.
точек) называют полным
двоичным деревом.
Нижнюю точку называют корнем. У каждой вершины есть
два сына (две вершины, в которые идут стрелки) -
левый и правый. У всякой вершины, кроме
корня, есть единственный отец.
Пусть выбрано некоторое конечное множество вершин полного
двоичного дерева, содержащее вместе с каждой вершиной и всех ее
предков. Пусть на каждой вершине этого множества написано
значение фиксированного типа  (то есть задано отображение
множества вершин в множество значений типа
(то есть задано отображение
множества вершин в множество значений типа  ). То, что
получится, будем называть
). То, что
получится, будем называть  -деревом. Множество всех
-деревом. Множество всех  -деревьев обозначим
-деревьев обозначим  .
.
Рекурсивное определение. Всякое непустое  -дерево
разбивается на три части: корень (несущий пометку из
-дерево
разбивается на три части: корень (несущий пометку из  ), левое и правое поддеревья (которые могут быть пустыми). Это разбиение устанавливает взаимно однозначное соответствие между множеством непустых
), левое и правое поддеревья (которые могут быть пустыми). Это разбиение устанавливает взаимно однозначное соответствие между множеством непустых  -деревьев и произведением
-деревьев и произведением 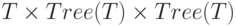 .
Обозначив через empty пустое дерево, можно написать
.
Обозначив через empty пустое дерево, можно написать

Поддеревья. Высота
Фиксируем некоторое  -дерево. Для каждой его
вершины
-дерево. Для каждой его
вершины  определено ее левое поддерево (левый сын
вершины
определено ее левое поддерево (левый сын
вершины  и все его потомки), правое поддерево
(правый сын вершины
и все его потомки), правое поддерево
(правый сын вершины  и все его потомки)
и поддерево с корнем в x (вершина
и все его потомки)
и поддерево с корнем в x (вершина  и все ее потомки).
и все ее потомки).
Левое и правое поддеревья вершины  могут быть пустыми, а поддерево с корнем в
могут быть пустыми, а поддерево с корнем в  всегда непусто (содержит по крайней мере
всегда непусто (содержит по крайней мере  ). Высотой поддерева будем считать максимальную длину цепи
). Высотой поддерева будем считать максимальную длину цепи 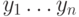 его вершин, в которой
его вершин, в которой 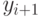 - сын
- сын  для всех
для всех  . ( Высота дерева из одного корня равна единице,
высота пустого дерева - нулю.)
. ( Высота дерева из одного корня равна единице,
высота пустого дерева - нулю.)
Упорядоченные T-деревья
Пусть на множестве значений типа  фиксирован порядок.
Назовем
фиксирован порядок.
Назовем  -дерево упорядоченное дерево, если выполнено такое свойство: для любой вершины
-дерево упорядоченное дерево, если выполнено такое свойство: для любой вершины  все
пометки в ее левом поддереве меньше пометки в
все
пометки в ее левом поддереве меньше пометки в 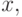 а все
пометки в ее правом поддереве больше пометки в
а все
пометки в ее правом поддереве больше пометки в  .
.
14.1.1. Доказать, что в упорядоченном дереве все пометки различны.
Указание. Индукция по высоте дерева.
Представление множеств с помощью деревьев
Каждое дерево будем считать представлением множества всех пометок на его вершинах. При этом одно и то же множество может иметь различные представления.
Благодаря упорядоченности каждый элемент может легко "найти свое место" в дереве: придя в какую-то вершину и сравнив себя с тем, кто там находится, элемент решает, идти ему налево или направо.
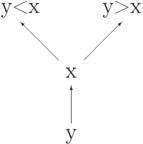
Всюду далее мы предполагаем,
что на значениях типа  задан порядок, и рассматриваем только упорядоченные деревья.
задан порядок, и рассматриваем только упорядоченные деревья.


