Представление множеств. Деревья. Сбалансированные деревья.

14.2.4. В сбалансированное дерево добавили или из него удалили лист. Доказать, что можно восстановить сбалансированность с помощью нескольких вращений, причем их число не больше высоты дерева.

Решение. Будем доказывать более общий факт:

Лемма. Если в сбалансированном дереве одно из его поддеревьев заменили на сбалансированное дерево , причем высота отличается от высоты не более чем на , то полученное такой "прививкой" дерево можно превратить в сбалансированное вращениями (причем количество вращений не превосходит высоты, на которой делается прививка).

Частным случаем прививки является замена пустого поддерева на лист или наоборот, так что достаточно доказать эту лемму.

Доказательство леммы. Индукция по высоте, на которой делается прививка. Если она происходит в корне (заменяется все дерево целиком), то все очевидно ("привой" сбалансирован по условию). Пусть заменяется некоторое поддерево, например, левое поддерево некоторой вершины . Возможны два случая.

1. После прививки сбалансированность в вершине не нарушилась (хотя, возможно, нарушилась сбалансированность в предках : высота поддерева с корнем в могла измениться). Тогда можно сослаться на предположение индукции, считая, что мы прививали целиком поддерево с корнем в .
2. Сбалансированность в нарушилась. При этом разница высот равна (больше она быть не может, так как высота отличается от высоты не более чем на ). Разберем два варианта.
   

   
   
   1. Выше правое (не заменявшееся) поддерево вершины . Пусть высота левого (т.е. ) равна , правого - . Высота старого левого поддерева вершины (т.е. была равна . Поддерево с корнем имело в исходном дереве высоту , и эта высота не изменилась после прививки.

      По предыдущей задаче вращение преобразует поддерево с корнем в в сбалансированное поддерево высоты или . То есть высота поддерева с корнем - в сравнении сего прежней высотой - не изменилась или уменьшилась на , и мы можем воспользоваться предположением индукции.
   2. Выше левое поддерево вершины . Пусть высота левого (т.е. ) равна , правого - . Высота старого левого поддерева (т.е. ) была равна . Поддерево с корнем в исходном дереве имело высоту , после прививки она стала равна . После подходящего вращения (см.предыдущую задачу) поддерево с корнем в станет сбалансированным, его высота будет равна или , так что изменение высоты по сравнению с высотой поддерева с корнем в дереве не превосходит и можно сослаться на предположение индукции.

14.2.5. Составить программы добавления и удаления элементов, сохраняющие сбалансированность. Число действий не должно превосходить . Разрешается хранить в вершинах дерева дополнительную информацию, необходимую при балансировке.

Решение. Будем хранить для каждой вершины разницу между высотой ее правого и левого поддеревьев:

(2) После преобразований мы должны также изменить соответственно значения в массиве diff. Для этого достаточно знать высоты деревьев 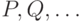с точностью до константы, поэтому можно предполагать, что одна из высот равна нулю.

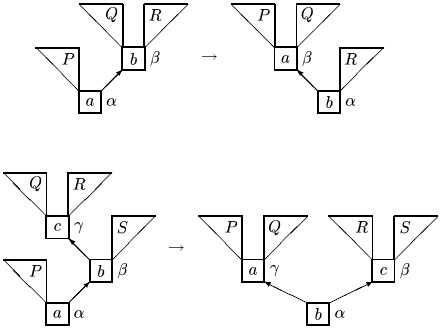
Вот процедуры вращений:

procedure SR (a:integer); {малое правое вращение с корнем a}
| var b: 1..n; val_a,val_b: T; h_P,h_Q,h_R: integer;
begin
| b := right [a]; {b <> null}
| val_a := val [a]; val_b := val [b];
| h_Q := 0; h_R := diff[b]; h_P := (max(h_Q,h_R)+1)-diff[a];
| val [a] := val_b; val [b] := val_a;
| right [a] := right [b] {поддерево R}
| right [b] := left [b] {поддерево Q}
| left [b] := left [a] {поддерево P}
| left [a] := b;
| diff [b] := h_Q - h_P;
| diff [a] := h_R - (max (h_P, h_Q) + 1);
end;

procedure BR(a:integer);{большое правое вращение с корнем a}
| var b,c: 1..n; val_a,val_b,val_c: T;
|     h_P,h_Q,h_R,h_S: integer;
begin
| b := right [a]; c := left [b]; {,c <> null}
| val_a := val [a]; val_b := val [b]; val_c := val [c];
| h_Q := 0; h_R := diff[c]; h_S := (max(h_Q,h_R)+1)+diff[b];
| h_P := 1 + max (h_S, h_S-diff[b]) - diff [a];
| val [a] := val_c; val [c] := val_a;
| left [b] := right [c] {поддерево R}
| right [c] := left [c] {поддерево Q}
| left [c] := left [a] {поддерево P}
| left [a] := c;
| diff [b] := h_S - h_R;
| diff [c] := h_Q - h_P;
| diff [a] := max (h_S, h_R) - max (h_P, h_Q);
end;

Левые вращения (большое и малое) записываются симметрично.

Процедуры добавления и удаления элементов пишутся как раньше, но только добавление и удаление должно сопровождаться коррекцией массива diff и восстановлением сбалансированности.

При этом используется процедура с такими свойствами:

дано: левое и правое поддеревья вершины с номером a сбалансированы, в самой вершине разница высот не больше 2, в поддереве с корнем a массив diff заполнен правильно;

надо: поддерево с корнем a сбалансировано и массив diff соответственно изменен, d - изменение его высоты (равно 0 или -1); в остальной части все осталось как было - в частности, значения diff

procedure balance (a: integer; var d: integer);
begin {-2 <= diff[a] <= 2}
| if diff [a] = 2 then begin
| | b := right [a];
| | if diff [b] = -1 then begin
| | | BR (a); d := -1;
| | end else if diff [b] = 0 then begin
| | | SR (a); d := 0;
| | end else begin {diff [b] = 1}
| | | SR (a); d := - 1;
| | end;
| end else if diff [a] = -2 then begin
| | b := left [a];
| | if diff [b] = 1 then begin
| | | BL (a); d := -1;
| | end else if diff [b] = 0 then begin
| | | SL (a); d := 0;
| | end else begin {diff [b] = -1}
| | | SL (a); d := - 1;
| | end;
| end else begin {-2 < diff [a] < 2, ничего делать не надо}
| | d := 0;
| end;
end;