Оптимальное кодирование
12.1. Коды
Имея  символов, мы можем кодировать каждый из них
символов, мы можем кодировать каждый из них  битами, поскольку существует
битами, поскольку существует  комбинаций
из
комбинаций
из  битов. Например, можно закодировать
битов. Например, можно закодировать 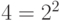 символа А, Г, Т, Ц (используемые при записи геномов) двухбитовыми
комбинациями
символа А, Г, Т, Ц (используемые при записи геномов) двухбитовыми
комбинациями  ,
,  ,
,  и
и  . Другой пример:
последовательностями из
. Другой пример:
последовательностями из  битов (байтами) можно
закодировать
битов (байтами) можно
закодировать  символов (и этого хватает на латинские
и русские буквы, знаки препинания и др.).
символов (и этого хватает на латинские
и русские буквы, знаки препинания и др.).
Более формально: пусть нам дан алфавит,
то есть конечное множество, элементы которого называются символами или буквами этого алфавита. Кодом для алфавита  называется функция (таблица)
называется функция (таблица)  ,
которая для каждого символа
,
которая для каждого символа  из
из  указывает двоичное
слово
указывает двоичное
слово 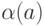 , называемое кодовым словом, или просто кодом
этого символа. ( Двоичное слово - конечная
последовательность нулей и единиц.)
Не требуется, чтобы коды всех символов имели равные длины.
, называемое кодовым словом, или просто кодом
этого символа. ( Двоичное слово - конечная
последовательность нулей и единиц.)
Не требуется, чтобы коды всех символов имели равные длины.
Мы допускаем, чтобы разные символы имели одинаковые коды.
Согласно нашему определению, разрешается все буквы алфавита
закодировать словом  (и даже пустым словом) - но,
конечно, такой код будет бесполезен. Хороший код должен
позволять декодирование (восстановление последовательности
символов по ее коду).
(и даже пустым словом) - но,
конечно, такой код будет бесполезен. Хороший код должен
позволять декодирование (восстановление последовательности
символов по ее коду).
Формально это определяется так. Пусть фиксирован алфавит  и код
и код  для этого алфавита. Для каждого слова
для этого алфавита. Для каждого слова  в алфавите
в алфавите  (то есть для любой конечной
последовательности букв алфавита
(то есть для любой конечной
последовательности букв алфавита  ) рассмотрим двоичное слово
) рассмотрим двоичное слово  , которое получается, если записать подряд коды всех букв из
, которое получается, если записать подряд коды всех букв из  (без каких-либо разделителей). Код
(без каких-либо разделителей). Код  называется однозначным,
если коды различных слов различны:
называется однозначным,
если коды различных слов различны:  при
при  .
.
12.1.1.
Рассмотрим трехбуквенный алфавит 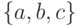 и код
и код 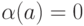 ,
, 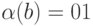 и
и  . Будет ли
этот код однозначным?
. Будет ли
этот код однозначным?
Решение. Нет, поскольку слова 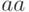 и
и  кодируются одинаково.
кодируются одинаково.
12.1.2.
Для того же алфавита рассмотрим код 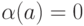 ,
,  и
и 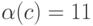 . Будет ли этот код однозначным?
. Будет ли этот код однозначным?
Решение. Будет. Чтобы доказать это, достаточно объяснить, как
можно восстановить слово  по его коду
по его коду  .
Если
.
Если  начинается с нуля, то ясно, что слово
начинается с нуля, то ясно, что слово  начинается
с
начинается
с  . Если
. Если  начинается с единицы, то
слово
начинается с единицы, то
слово  начинается с
начинается с  или с
или с  - чтобы узнать, с чего именно,
достаточно посмотреть на второй бит слова
- чтобы узнать, с чего именно,
достаточно посмотреть на второй бит слова  .
Восстановив первую букву слова
.
Восстановив первую букву слова  , мы забываем о ней и о ее
коде, и продолжаем все сначала.
, мы забываем о ней и о ее
коде, и продолжаем все сначала.
Верно и более общее утверждение. Назовем код префиксным,
если коды букв не являются началами друг
друга (слово 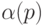 не является началом слова
не является началом слова 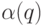 , если буквы
, если буквы  и
и  различны).
различны).
12.1.3. Доказать, что любой префиксный код является однозначным.
Решение. Декодирование можно вести слева направо. Первая буква восстанавливается однозначно: если для двух
букв  и
и  слова
слова 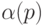 и
и 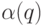 являются началами кода, то
одно из слов
являются началами кода, то
одно из слов 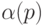 и
и 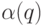 является началом другого, что невозможно для префиксного кода. И так далее.
является началом другого, что невозможно для префиксного кода. И так далее.
12.1.4. Привести пример однозначного кода, не являющегося префиксным.
Указание.
Пусть 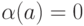 ,
, 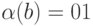 ,
, 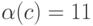 .
Этот код является "суффиксным", но не префиксным.
.
Этот код является "суффиксным", но не префиксным.
12.1.5. Найти таблицу для азбуки Морзе. Объяснить, почему ее можно использовать на практике, хотя она не является ни префиксным, ни даже однозначным кодом.
