Генетическое программирование
6.6. Фитнесс-функция в генетическом программировании
В отличие от генетических алгоритмов, где часто при поиске экстремумов в качестве фитнесс-функции используется исходная целевая функция, в ГП фитнесс-функция обычно определяет меру близости между реальными 
и требуемыми 
выходными значениями (например, при использовании ГП в имвольной регрессии ). Поэтому в качестве фитнесс-функции часто используется абсолютная или квадратичная ошибка.
В этом случае фитнесс-функция использует обучающее множество данных, на котором выполняется обучение системы. С помощью фитнесс-функции в процессе обучения реализуется обратная связь, которая показывает насколько хорошо данная особь-программа реализует необходимую функцию на обучающем множестве. Для этого можно использовать различные виды фитнес-функций, некоторые из которых мы рассмотрим ниже.
"Непрерывной" (continuous) фитнесс-функцией называют [5] функцию вычисления фитнесс-значений, в которой малое улучшение в обучении программы вызывает малые улучшения измеряемых фитнесс-значений и большие улучшения в обучении связаны соответственно с большими изменениями (в сторону улучшения) фитнесс-значений. В [5] отмечается, что такая "непрерывность" является важным свойством, так как позволяет ГП итеративно улучшать программы в процессе эволюции.
"Стандартизованой" [5] фитнесс-функцией называют преобразованную фитнесс-функцию, которая лучшим особям приписывает нулевое значение.
"Нормализованной" [5] фитнесс-функцией называют преобразованную фитнесс-функцию, которая для всех особей дает значения в интервале (0,1).
Рассмотрим следующий пример [5] с обучающей выборкой, представленной табл.6.7. Каждая строка таблицы определяет один элемент 
обучающей выборки. Необходимо в процессе эволюции построить программу (или формулу в случае символьной регрессии), которая для каждого входного значения x вычисляет необходимое (в соответствии с табл.6.5) значение y (фактически нам необходимо реализовать функцию 
).
Рассмотрим в качестве фитнесс-функции ошибку в метрике абсолютных значений 
, где суммирование выполняется по обучающей выборке. Эта фитнесс-функция соответствует первому определению "непрерывной", поскольку чем ближе значения к , тем меньше значение фитнесс-функции. Приведенная фитнесс-функция является также стандартизованной, так как в случае идеального решения дает нулевое значение.
Часто в качестве фитнесс-функции также используют квадратичную ошибку 
.Таблица 6.8 показывает различие для этих двух фитнесс-функций в том случае, если на некотором (промежуточном) этапе в качестве особи оценивается (плохо обученная) программа, реализующая функцию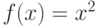 
.
Мы рассмотрели использование в качестве фитнесс-функции ошибки в двух метриках, которые характерны для применения ГП в качестве символьной регрессии, что будет детальнее рассмотрено в разделе 6.8.
| № | Вход 
|
Выход 
|
Выход 
|
Ошибка 
|
Ошибка 
|
|---|---|---|---|---|---|
| 1 | 1 | 2 | 1 | 1 | 2 |
| 2 | 2 | 6 | 4 | 2 | 4 |
| 3 | 4 | 20 | 16 | 4 | 16 |
| 4 | 7 | 56 | 49 | 7 | 49 |
| 5 | 9 | 90 | 81 | 9 | 81 |
| Общая ошибка | 23 | 151 | |||
Подобный подход применяется также во многих других задачах, где используются следующие фитнесс-функции:
- число правильно отображаемых пикселов в задачах обработки изображений;
- число столкновений робота со стенами при обучении обхода препятствия;
- число правильно классифицируемых примеров в задачах классификации;
- ошибка между реальными и ожидаемыми значениями в задачах прогнозирования;
- приз победителя в игровых задачах;
- количество "пищи", найденной агентом, в многоагентных системах ("искусственная жизнь" и т.п.)
Естественно разработано множество фитнесс-функций других типов, их вид существенно зависит от исследуемой проблемы, а применение ГП не ограничивается задачами символьной регрессии. Кроме приведенных стандартных разработано много других методов определения фитнесс-функции, в частности теоретико-игровых и основанных на идее коэволюции, где особи соревнуются между собой без явного вычисления значений. В некоторых случаях, кроме близости решений, учитываются и другие критерии, например, длина или время выполнения программы. В этом случае говорят о многокритериальных фитнесс-функциях.