Эволюционные вычисления
[+]
Московский государственный университет путей сообщения
Опубликован: 10.10.2014 | Доступ: свободный | Студентов: 869 / 193 | Длительность: 22:10:00
Тема: Алгоритмы и дискретные структуры
Специальности: Программист, Архитектор программного обеспечения
Лекция 6:

Генетическое программирование
A
|
версия для печати
< Лекция 5 || Лекция 6: 123456789101112 || Лекция 7 >

Контрольные вопросы

  1. Чем отличаются терминальное и функциональное множества?
  2. Какие структуры используются для представления программ в ГП?
  3. Опишите древовидное представление программы.
  4. Какой тип памяти используется в древовидном представлении?
  5. Опишите линейное представление программы.
  6. Опишите представление программы в виде графа.
  7. Какие два метода используются в инициализации древовидных структур?
  8. Как производится инициализация линейных структур?
  9. Какие виды кроссинговера вы знаете для древовидных структур?
  10. Как выполняется кроссинговер на линейных структурах?
  11. Какие виды кроссинговера вы знаете для графоподобных структур?
  12. Какие виды мутации вы знаете для древовидных структур?
  13. Как производится мутация на линейных структурах?
  14. Как можно определить фитнесс-функцию в ГП?
  15. Что такое интроны?
  16. Приведите общий алгоритм ГП.
  17. Чем отличается символьная регрессия от обычной?
  18. Как можно в ГП использовать принцип модульного построения программ?

Упражнения

  1. Разработать эволюционный алгоритм, реализующий ГП для нахождения заданной по варианту функции (таб. 6.14).
    • Структура для представления программы – древовидное представление.
    • Терминальное множество: переменные x_1, x_2, x_3, \dots,x_n,, и константы в соответствии с заданием по варианту.
    • Функциональное множество:+, -, *, /, abs(), \sin(), \cos(), \exp(), возведение в степень,
    • Фитнесс-функция – мера близости между реальными значениями выхода и требуемыми.
  2. Представить графически найденное решение на каждой итерации.
  3. Сравнить найденное решение с представленным в условии задачи.
Таблица 6.14.
№ вв. Вид функции Кол-во первых N Промежуток исследования
1
f_1(x)=\sum_{i=1}^n x_i^2
 10
-5,12\le x_i\le 5,12
2
f_{la}(x)=\sum_{i=1}^n i\cdot x_i^2
 9
-5,12\le x_i\le 5,12
3
f_{1b}(x)=\sum_{i=1}^n\left(\sum_{j=1}^i x_j\right)^2
 8
-5,536\le x_i\le 65,536
4
f_2(x)=\sum_{i=1}^{n-1} 100\cdot (x_{i+1}-x_i^2)^2+(1-x_i)^2)
 7
-2,048\le x_i\le 2,048
5
f_6(x)=10\cdot n+\sum_{i=1}^n(x_i^2-10\cdot \cos(2\cdot\pi\cdot x_i))
 9
-5,12\le x_i\le 5,12
6
f_7(x)=\sum_{i=1}^n -x_i\cdot \sin(\sqrt{|x_i|})
 10
-500\le x_i\le 500
7
f_8(x)=\sum_{i=1}^n \frac{x_i^2}{4000}-\prod_{i=1}^n\cos\left(\frac{x_i}{\sqrt{i}\right)+10
 5
-600\le x_i\le 600
8
f_9(x)=\sum_{i=1}^n|x_i|^{(i+1)}
 8
-1\le x_i\le 1
9
f_{10}(x)=-a\cdot e^{-b\cdot \sqrt{\frac{\sum_{i=1}^n x_i^2}{n}}}-e^{\frac{\sum_{i=1}^n cos(c\cdot x_i)}{n}}+a+e^1;\\a=20;b=0,2;c=2\cdot \pi
 4
-2.768\le x_i\le 32.768
10
f_{11}(x)=-\sum_{i=1}^m c_i\cdot(e^{-\frac{\|x-A(i)\|^2}{\pi}}\cdot\cos\left(\pi\cdot\|\bar x-A(i)\|^2)),\\m=5;A_i,C_i\ne 0
 4
0\le x_i\le 10
11
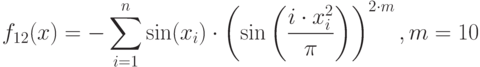f_{12}(x)=-\sum_{i=1}^n \sin(x_i)\cdot\left(\sin\left(\frac{i\cdot x_i^2}{\pi} \right ) \right)^{2\cdot m},\\ m=10
 5
0\le x_i\le \pi
12
f_{Bran}(x_1,x_2)=a\cdot(x_2-b\cdot x_1^2+c\cdotx_1-d)^2+e\cdot(1-f)\cdot(x_1)+e,\\a=1,b=\frac{5,1}{4\cdot \pi^2},c=\frac{5}{\pi},d=6,e=10,f=\frac{1}{8\cdot\pi}
 2
-5\le x_1\le 10,\ 0\le x_2\le \15
13
f_{Easo}(x_1,x_2)=-\cos(x_1)\cdot\cos(x_2)\cdot e^{-((x_1-\pi)^2+(x_2-\pi)^2)}
 2
-100\le x_i\le 100
14
f_{Gold}(x_1,x_2)=(1+(x_1+x_2+1)^2\cdot(19-14x_1+3x_1^2-14x_2+6x_1x_2+3x_2^2))\cdot(30+(2x_1-3x_2)^2\cdot(18-32x_1+12x_1^2+48x_2-36x_1x_2+27x_2^2))
 2
-2\le x_i\le 2
15 f_{Sixh}(x_1,x_2)=(4-2.1\cdot x_1^2+x_1^{4/3})\cdot x_1^2+x1\cdot x_2+(-4+4\cdot x_2^2)\cdot x_2^2; 2
-3\le x_1\le 3,-2\le x_2\le2

Краткие итоги:

  • изложены основы ГП, основной алгоритм ГП и его параметры;
  • описаны основные формы представления ГП: древовидное, линейное, графоподобное;
  • рассмотрены различные методы инициализации начальной популяции в ГП;
  • описаны генетические операторы кроссинговера и мутации на различных формах представления ГП;
  • изложен на основе ГП метод символьной регрессии;
  • рассмотрено использование модульного построения в ГП.
Дальше >>
< Лекция 5 || Лекция 6: 123456789101112 || Лекция 7 >

Вопросы и ответы

вопросов: 0