Генетическое программирование
6.4. Кроссинговер в генетическом программировании
В начальной популяции особи (потенциальные решения), как правило, имеют низкие (плохие) значения фитнесс-функции. В процессе эволюции с помощью генетических операторов популяция развивается и значения фитнесс-функции улучшаются. В ГП используются те же, что и в ГА, генетические операторы кроссинговера, мутации и репродукции. Отметим, что в терминах машинного обучения они соответствуют операторам поиска решения. Далее мы рассмотрим выполнение генетических операторов на ранее определенных структурах.
6.4.1. Выполнение кроссинговера на древовидных структурах
Для древообразной формы представления используются следующие три основные операторы кроссинговера (ОК):
- узловой ОК;
- кроссинговер поддеревьев;
- смешанный.
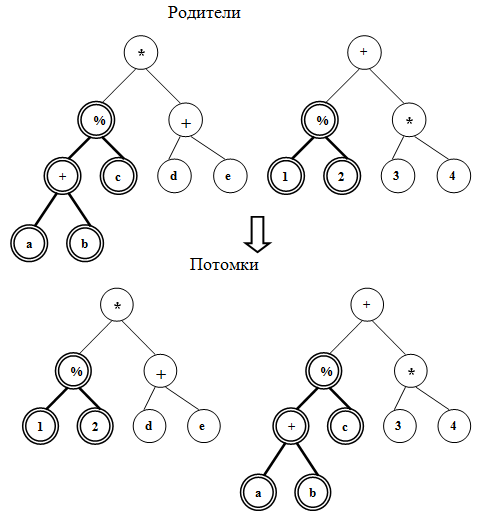
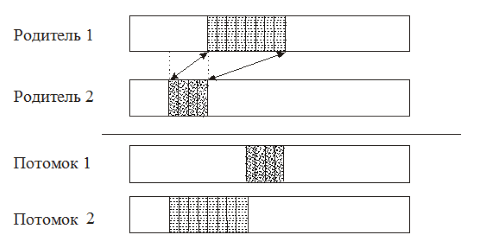
В узловом операторе кроссинговера выбираются два родителя (два дерева) и узлы в этих деревьях. Первый родитель называется доминантом, второй – рецессивом. Узлы в деревьях могут быть разного типа. Поэтому сначала необходимо убедиться, что выбранные узлы у родителей являются взаимозаменяемыми. Если узел во втором родителе не соответствует типу узла первого родителя, то случайным образом выбирается другой узел во втором родителе, который опять подлежит проверке на предмет совместимости. Далее производится обмен узлов.
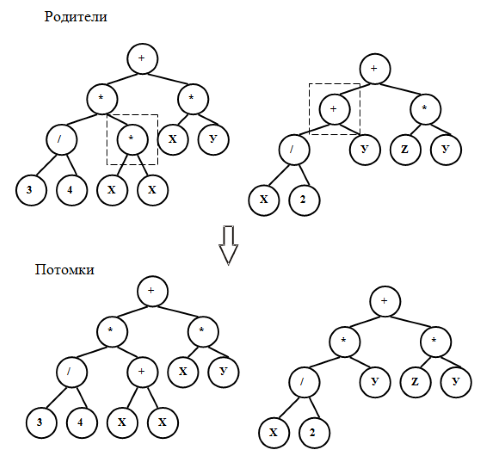
Рассмотрим ОК на следующем примере, представленном на рис.6.7 для родительских особей: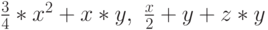
В кроссинговере поддеревьев родители обмениваются не узлами, а определяемыми ими поддеревьями. Оператор выполняется следующим образом:
- Выбираются родители (один – доминантный, другой – рецессивный). Далее необходимо убедиться, что выбранные узлы взаимозаменяемы, т.е. принадлежат одному типу. Иначе, как и в предыдущем случае, в рецессивном дереве выбирается другой узел с последующей проверкой.
- Затем производится обмен поддеревьев, которые определены этими узлами.
- Вычисляется размер ожидаемых потомков. Если ожидаемый размер (сложность потомка) не превышает заданный порог, такой обмен ветвями запоминается. На рис.6.8показан пример выполнения этого ОК.
Этот тип ОК является основным. При этом под размером (под)дерева понимается, как и ранее, либо его высота, либо число его вершин.
При смешанном операторе кроссинговера для некоторых узлов выполняется узловой ОК, а для других - кроссинговер поддеревьев.
Отметим, что выполнение кроссинговера на древовидных структурах выполняется достаточно просто с помощью  -выражений, что показано в таблице 6.4. Например, кроссинговер поддеревьев сводится к обмену "скобками", которые здесь соответствуют поддеревьям.
-выражений, что показано в таблице 6.4. Например, кроссинговер поддеревьев сводится к обмену "скобками", которые здесь соответствуют поддеревьям.
В таблице 6.5 приведены типовые операторы кроссинговера для древовидных структур[3,8].
| Наименование | Описание производимых действий |
|---|---|
| Кроссинговер обмена поддеревьев | Обмен поддеревьями родителей |
| Само-кроссинговер | Обмен поддеревьями в одном родителе |
| Модульный кроссинговер | Обмен модулями (фрагментами) родителей |
| Контекстно-сохраняющий кроссинговер | Полный обмен поддеревьями, если он согласуется с контекстом, иначе частичный обмен |
6.4.2. Кроссинговер на линейных структурах
Скрещивание на линейных структурах выполняется достаточно просто. Здесь у родителей выполняется обмен линейными сегментами, как это показано на рис.6.9.
При этом в каждом из двух родителей выбирается сегмент, начиная со случайной позиции и имеющий случайную длину. Далее производится обмен выбранных сегментов программ. Если размер хотя бы одного из потомков превышает некоторый порог, то результаты ОК аннулируются. При этом точки скрещивания выбираются только между операторами.
6.4.3. Выполнение кроссинговера для графоподобных структур
Кроссинговер комбинирует генетический материал из двух родительских программ путем обмена некоторых частей программ. ОК для этой модели может быть реализован двумя способами.
Первый способ похож на кроссинговер поддеревьев, который определен на древообразных структурах путем обмена поддеревьев. Здесь обмен производится подграфами, как это показано на рис.6.10.
При этом в каждой особи-родителе выбирается случайным образом множество смежных узлов и производится обмен двух подграфов между этими подграфами.
Второй тип кроссинговера выполняет линейный ОК. Здесь для каждого родителя выбирается линейный сегмент (в одном узле графа), начинающийся со случайной позиции данного сегмента и имеющий случайную длину. Далее, как обычно, производится обмен этими линейными сегментами. Если размер хотя бы одного потомка превышает некоторый порог, то результаты ОК аннулируются и выполняется обмен равными сегментами меньшей длины.
Обычно линейный ОК выполняется в вероятностью 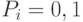 . Пример выполнения этого ОК представлен на рис.6.11. Как правило, в процессе эволюции используются ОК обоих типов. В целом ОК выполняется следующим образом:
. Пример выполнения этого ОК представлен на рис.6.11. Как правило, в процессе эволюции используются ОК обоих типов. В целом ОК выполняется следующим образом:
- Выбор точки скрещивания
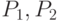 в обоих родителях
в обоих родителях - Выбор с заданной вероятностью типа ОК ( для 1-го типа с вероятностью
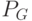 , для 2-го с вероятностью
, для 2-го с вероятностью 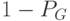 ).Если выбран 1-й тип то переход на п.3, иначе на п.4.
).Если выбран 1-й тип то переход на п.3, иначе на п.4. - Если размер потомка не превышает порог, то выполнить ОК 1-го типа, переход на п.5.
- Если размер потомка не превышает порог, то выполнить ОК 2-го типа.
- Конец.