Введение.Основы генетических алгоритмов
Влияние мутации
Напомним, что оператор мутации (ОМ) есть случайное изменение элемента в стринге с вероятностью 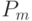 . Очевидно, что для того чтобы схема
. Очевидно, что для того чтобы схема  выжила, все определенные позиции должны выжить. Поскольку один ген выживает с вероятностью
выжила, все определенные позиции должны выжить. Поскольку один ген выживает с вероятностью 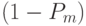 , то данная схема выживает, когда каждая из O(H) фиксированных позиций схемы выживает. Умножая вероятность выживания
, то данная схема выживает, когда каждая из O(H) фиксированных позиций схемы выживает. Умножая вероятность выживания 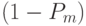
 раз, получим, что вероятность выживания при ОМ равна
раз, получим, что вероятность выживания при ОМ равна  . Для малых величин
. Для малых величин 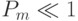 это выражение может быть аппроксимировано как
это выражение может быть аппроксимировано как 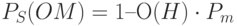 .
.
Из этого следует, что схема  дает ожидаемое число особей в следующей популяции после выполнения всех генетических операторов ОР, ОК и ОМ согласно следующей формуле:
дает ожидаемое число особей в следующей популяции после выполнения всех генетических операторов ОР, ОК и ОМ согласно следующей формуле:
![m(H,t+1)>m(H,t)\cdot \frac{f(H)}{\bar f}[1-P_m\frac{L(H)}{1-n}-O(H)\cdot P_m]](/sites/default/files/tex_cache/719cc48450184792ea29f2d5070c2c3b.png) |
( 1.5) |
Этот важный результат известен какфундаментальная теорема ГА. Учитывая (1.3) ее можно также сформулировать следующим образом.
Теорема 1.1. Схемы малого порядка, малой определенной длины и со значением фитнесс-функции выше средней формируют растущее по показательному закону число своих представителей в последующих поколениях генетического алгоритма.
На основании приведенных результатов была выдвинута гипотеза о строительных блоках.
Гипотеза 1.1. Генетический алгоритм стремится достичь близкого к оптимальному результата за счет комбинирования хороших схем (со значением фитнесс-функции выше средней, малого порядка и определенной длины).
Такие схемы называются строительными блоками. В соответствии с этим оптимальное решение строится путем объединения наилучших из полученных на текущий момент частичных решений. Оператор скрещивания на двоичных стрингах не слишком часто уничтожает схемы малой определенной длины, однако ликвидирует схемы большой длины. Однако, не смотря на губительность операторов скрещивания и мутации для схем большого порядка и определенной длины, число обрабатываемых схем настолько велико, что даже в относительно малом числе особей в популяции генетический алгоритм дает неплохие результаты.
Несмотря на то, что для доказательства этой гипотезы были предприняты значительные усилия, строгого доказательства получено не было, и в большинстве нетривиальных приложений опираются на эмпирические результаты.
Далее проиллюстрируем приведенные результаты. Вернемся к примеру Голдберга определения 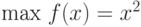 . В дополнение к имеющимся таблицам рис 1.3 пусть имеется 3 конкретные схемы
. В дополнение к имеющимся таблицам рис 1.3 пусть имеется 3 конкретные схемы  =1*****,
=1*****,  =*10** и
=*10** и 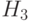 =1***0, описанные в табл.1.2.
=1***0, описанные в табл.1.2.
Рассмотрим сначала схему  . При репродукции стринги копируются с вероятностью, определенной согласно величине их фитнесс-функции. Из табл. 1.1 видно, что стринги 2,4 покрываются схемой
. При репродукции стринги копируются с вероятностью, определенной согласно величине их фитнесс-функции. Из табл. 1.1 видно, что стринги 2,4 покрываются схемой  . После выполнения репродукции мы видим в табл. 1.3 (строка
. После выполнения репродукции мы видим в табл. 1.3 (строка  ), что получены три копии и стринг 3 также вошел в популяцию.
), что получены три копии и стринг 3 также вошел в популяцию.
| Схема | Перед репродукцией | Представители стрингов | Среднее значение ЦФ схемы 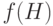
|
|---|---|---|---|
 |
1**** | 2,4 | 469 |
 |
*10** | 2,3 | 320 |
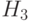 |
1***0 | 2 | 576 |
Проверим, соответствует ли это число фундаментальной теореме схем. Согласно теории мы ожидаем 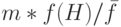 копий. Вычисляя среднее значение ЦФ
копий. Вычисляя среднее значение ЦФ  , получаем
, получаем 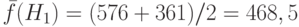 . Разделив это число на среднее значение ЦФ популяции
. Разделив это число на среднее значение ЦФ популяции 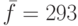 и умножив его на число
и умножив его на число 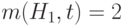 стрингов, покрываемых
стрингов, покрываемых  на шаге
на шаге  , получаем ожидаемое число стрингов, покрываемых
, получаем ожидаемое число стрингов, покрываемых  на шаге
на шаге  , т.е.
, т.е.  .
.
| Схема | После репродукции | После всех операторов | ||||
|---|---|---|---|---|---|---|
| Ожидаемое число стрингов | Действительное число стрингов | Представители стрингов | Ожидаемое число стрингов | Действительное число стрингов | Представители стрингов | |
 |
3,20 | 3 | 2, 3, 4 | 3,20 | 3 | 2, 3, 4 |
 |
2,18 | 2 | 2, 3 | 1,64 | 2 | 2, 3 |
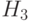 |
1,97 | 2 | 2, 3 | 0,0 | 1 | 4 |
Сравнивая это число с реальным числом копий 3, видим, что округление рассчитанного значения копий 3,2 дает их реальное число 3. Дальнейший анализ показывает, что в данном случае ОК не оказывает влияние на число стрингов, покрываемых схемой, так как определенная длина 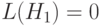 предотвращает разрыв схемы. Далее при мутации с вероятностью
предотвращает разрыв схемы. Далее при мутации с вероятностью 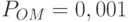 мы должны ожидать уменьшение числа стрингов на
мы должны ожидать уменьшение числа стрингов на  , что практически не оказывает влияния на окончательный результат. В итоге для схемы
, что практически не оказывает влияния на окончательный результат. В итоге для схемы  получаем ожидаемое увеличение числа особей до 3, что соответствует формуле (1.2).
получаем ожидаемое увеличение числа особей до 3, что соответствует формуле (1.2).
Рассмотрим теперь схемы  и
и 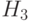 с двумя фиксированными позициями. Схема
с двумя фиксированными позициями. Схема  имеет также два представителя в начальной популяции (2,3) и две копии в следующей промежуточной популяции. Вычисляем
имеет также два представителя в начальной популяции (2,3) и две копии в следующей промежуточной популяции. Вычисляем  . Здесь
. Здесь 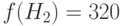 – среднее значение ЦФ схемы, а
– среднее значение ЦФ схемы, а 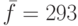 – среднее значение ЦФ популяции. Для
– среднее значение ЦФ популяции. Для 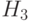 получаем только одно стринговое представление и
получаем только одно стринговое представление и  . Здесь 576 – среднее значение ЦФ схемы.
. Здесь 576 – среднее значение ЦФ схемы.
Заметим, что для конкретной схемы  представительство двух копий в популяции является хорошим результатом и он может случиться только один раз из 4-х возможных случаев
представительство двух копий в популяции является хорошим результатом и он может случиться только один раз из 4-х возможных случаев 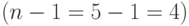 . Схема
. Схема 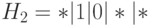 имеет реальную возможность дать новую копию. В результате, схема
имеет реальную возможность дать новую копию. В результате, схема  выживает с высокой вероятностью. Действительно, число стрингов, покрываемых
выживает с высокой вероятностью. Действительно, число стрингов, покрываемых  , равно
, равно 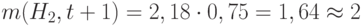 .
.
Для схемы 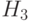 при высокой определенной длине
при высокой определенной длине 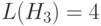 оператор ОК обычно разрушает эту схему. Поэтому ожидаемое число
оператор ОК обычно разрушает эту схему. Поэтому ожидаемое число  соответствует числу, получаемому по формуле (1.4).
соответствует числу, получаемому по формуле (1.4).
В соответствие с полученными результатами видно, что важнейшим аспектом является кодирование особей, которое должно обеспечить построение схем малого порядка малой определенной длины и со значениями фитнесс-функции выше среднего
Следующий простой пример показывает важность построения генома с учетом теорем схем.
Рассмотрим поиск максимума (для простоты при целочисленных значениях  и
и  ) функции
) функции 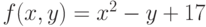 . Можно показать, что максимум
. Можно показать, что максимум  достигается при значениях
достигается при значениях 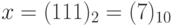 и
и  . Пусть
. Пусть  и
и 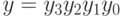 , где
, где  . Рассмотрим различное строение геномов. В первом случае пусть генотип представляет
. Рассмотрим различное строение геномов. В первом случае пусть генотип представляет 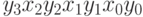 , во втором генотип определим как
, во втором генотип определим как 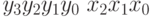 . Отметим, что в первом случае старшие разряды
. Отметим, что в первом случае старшие разряды  и
и  расположены в генотипе близко, а во втором варианте наоборот – достаточно далеко. Поскольку желательна короткая определенная длина, генетический алгоритм с геномом, в котором старшие разряды расположены близко, должен быть лучше по сравнению с геномом, где эти разряды стоят далеко друг от друга. Для первого случая
расположены в генотипе близко, а во втором варианте наоборот – достаточно далеко. Поскольку желательна короткая определенная длина, генетический алгоритм с геномом, в котором старшие разряды расположены близко, должен быть лучше по сравнению с геномом, где эти разряды стоят далеко друг от друга. Для первого случая 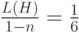 для схемы
для схемы  =01*****, где содержатся значения, наиболее важные для искомого решения. Для второго случая схема при тех же значениях имеет вид
=01*****, где содержатся значения, наиболее важные для искомого решения. Для второго случая схема при тех же значениях имеет вид  =0*****1, для которой
=0*****1, для которой 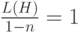 и поэтому необходимые значения старших битов
и поэтому необходимые значения старших битов  и
и  , скорее всего, при выполнении оператора кроссинговера будут "разорваны". Поэтому первый вариант генома предпочтительней.
, скорее всего, при выполнении оператора кроссинговера будут "разорваны". Поэтому первый вариант генома предпочтительней.
