Введение.Основы генетических алгоритмов
Фундаментальная теорема ГА
Влияние репродукции
Напомним, что в процессе репродукции хромосомы копируются в промежуточную популяцию согласно их значениям фитнесс-функции – хромосома  со значением
со значением 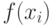 выбирается с вероятностью
выбирается с вероятностью  .
.
После репродукции мы ожидаем на следующем шаге получить m(H,t+1) двоичных стрингов, отображаемых схемой H. Известно, что
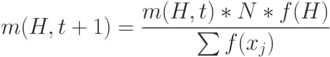 |
( 1.1) |
Это обусловлено тем, что:
- в среднем вероятность выбора стрингов, покрываемых схемой
 , определяется величиной
, определяется величиной 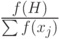 ,
, - число стрингов, представляемых
 , равно
, равно  ,
, - число стрингов в популяции равно
 .
.
Мы можем переписать эту формулу с учетом обозначения

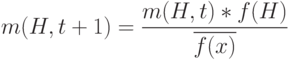 |
( 1.2) |
Другими словами, схемы "растут" как отношение среднего значения фитнесс-функции схемы к среднему значению фитнесс-функции популяции. Схема со значением фитнесс-функции выше средней в популяции имеет больше возможностей для копирования и наоборот. Правило репродукции Холланда гласит: "схема со значением фитнесс-функции выше среднего живёт и размножается, а со значением фитнесс-функции ниже среднего умирает".
Предположим, что схема  имеет значение выше среднего фитнесс-функции на величину
имеет значение выше среднего фитнесс-функции на величину 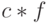 , где
, где  – константа. Тогда последнее выражение (1.2) можно модифицировать:
– константа. Тогда последнее выражение (1.2) можно модифицировать:
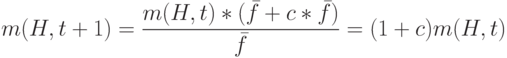
Начиная с 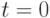 и предполагая, что
и предполагая, что  – величина постоянная, получаем следующее выражение числа особей промежуточной популяции, покрываемых схемой,
– величина постоянная, получаем следующее выражение числа особей промежуточной популяции, покрываемых схемой,
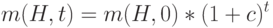 |
( 1.3) |
Это равенство описывает геометрическую прогрессию. Очевидно, что при  схема "размножается" а при
схема "размножается" а при  схема умирает.
схема умирает.
Далее рассмотрим влияние оператора кроссинговера на число особей в популяции, покрываемых схемой.
Влияние кроссинговера
Рассмотрим конкретный стринг 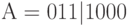 длины
длины 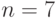 и две схемы, представляющие этот стринг:
и две схемы, представляющие этот стринг:  = *1*| ***0,
= *1*| ***0,  = ***| 10**
= ***| 10**
Здесь символ "|" , как обычно, обозначает точку кроссинговера  .
.
Очевидно, что схема  после кроссинговера с точкой
после кроссинговера с точкой  , скорее всего, будет уничтожена потому, что "1" в позиции 2 и "0" в позиции 7 попадут в разные новые стринги после кроссинговера. С другой стороны, ясно, что схема
, скорее всего, будет уничтожена потому, что "1" в позиции 2 и "0" в позиции 7 попадут в разные новые стринги после кроссинговера. С другой стороны, ясно, что схема  будет выживать, так как "10" в позициях 4,5 будут содержаться вместе в одном новом стринге. Хотя мы взяли точку скрещивания ОК случайно, ясно, что схема
будет выживать, так как "10" в позициях 4,5 будут содержаться вместе в одном новом стринге. Хотя мы взяли точку скрещивания ОК случайно, ясно, что схема  менее приспособлена к выживанию, чем схема
менее приспособлена к выживанию, чем схема  . Если точка скрещивания ОК выбирается случайным образом среди
. Если точка скрещивания ОК выбирается случайным образом среди 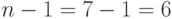 возможных позиций, то ясно, что схема
возможных позиций, то ясно, что схема  разрушается с вероятностью
разрушается с вероятностью
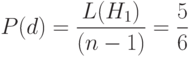
Очевидно, что эта же схема выживает с вероятностью
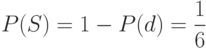
Аналогично, схема  имеет длину
имеет длину 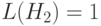 и вероятность её уничтожения
и вероятность её уничтожения 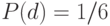 , а вероятность выживания схемы после применения ОК
, а вероятность выживания схемы после применения ОК  . Очевидно, что нижняя граница вероятности выживания схемы после применения ОК может быть вычислена для любой схемы. Так как схема выживает, когда точка ОК попадает вне "определенной длины" , вероятность выживания для простого ОК определяется по формуле
. Очевидно, что нижняя граница вероятности выживания схемы после применения ОК может быть вычислена для любой схемы. Так как схема выживает, когда точка ОК попадает вне "определенной длины" , вероятность выживания для простого ОК определяется по формуле 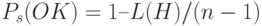 .
.
Если ОК выполняется посредством случайного выбора, например, с вероятностью 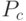 , то вероятность выживания схемы определяется так:
, то вероятность выживания схемы определяется так: 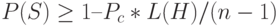 .
.
Очевидно, что это выражение уменьшается при 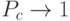 . Теперь мы можем асимптотически оценить совместный эффект операторов репродукции и кроссинговера. При независимости выполнения OP и OK можно получить следующее выражение:
. Теперь мы можем асимптотически оценить совместный эффект операторов репродукции и кроссинговера. При независимости выполнения OP и OK можно получить следующее выражение:
![m(H,t+1)\ge m(H,t)\frac{f(H)}{\bar f}[1-P_c\frac{L(H)}{n-1}]](/sites/default/files/tex_cache/caa10be56bb3e06d2ea6b25badc7b08c.png) |
( 1.4) |
Таким образом, число схем  в новой популяции зависит от двух факторов:
в новой популяции зависит от двух факторов:
- значение фитнесс-функции схемы выше или ниже значения ЦФ популяции;
-
схема имеет "длинную" или "короткую"
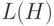 (определенную длину).
(определенную длину).
Видно, что схемы со значением ЦФ выше средней и с короткой длиной 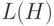 имеют возможность экспоненциального роста в новой популяции.
имеют возможность экспоненциального роста в новой популяции.
Далее рассмотрим влияние оператора мутации на число особей в популяции, покрываемых схемой.
