Введение.Основы генетических алгоритмов
1.4. Использование кода Грея в ГА
Рассмотренное двоичное представление вещественного числа имеет существенный недостаток: расстояние между вещественными числами (на числовой оси) часто не соответствует расстоянию (по Хеммингу) между их двоичными представлениями. Поэтому желательно получить двоичное представление, где близкие расстояния между хромосомами (двоичными представлениями) соответствовали близким расстояниям в проблемной области (в данном случае расстоянию на числовой оси) [3,14,15]. Это можно сделать, например, с помощью кода Грея. В таблице 1.1 приведен для примера код Грея для 4-х битовых слов.
| Двоичный код | Код Грея |
|---|---|
| 0000 | 0000 |
| 0001 | 0001 |
| 0010 | 0011 |
| 0011 | 0010 |
| 0100 | 0110 |
| 0101 | 0111 |
| 0110 | 0101 |
| 0111 | 0100 |
| 1000 | 1100 |
| 1001 | 1101 |
| 1010 | 1111 |
| 1011 | 1110 |
| 1100 | 1010 |
| 1101 | 1011 |
| 1110 | 1001 |
| 1111 | 1000 |
Заметим, что в коде Грея соседние двоичные слова отличаются на один бит (расстояние по Хеммингу равно 1).
Рассмотрим алгоритмы преобразования двоичного числа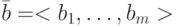 
в код Грея 
и наоборот.
Здесь параметр m определяет разрядность двоичного числа. Существует и другая, матричная, процедура преобразования в код Грея. Например, для 
матрицы
![A=\left[\begin{matrix}1000\\1100\\0110\\0011\end{matrix}\right] \mbox{и}\quad A^{-1}=\left[\begin{matrix}1000\\1100\\1110\\1111\end{matrix}\right]](/sites/default/files/tex_cache/999e336a3edbe04db2f6524b42cce8c2.png)
позволяют выполнять следующие преобразования:
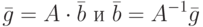
где умножение матриц выполняются в арифметике по mod 2.
Отметим, что применение кода Грея прежде всего оправдано при использовании операторов мутации.