Совокупности и отношения

Совокупности и отношения

Часто, и не только в математике, рассматриваются совокупности элементов, объектов или процессов, объединенных какими-то общими признаками.

Множество - это совокупность элементов реального или идеального происхождения, различимых между собой, объединяемых по некоторому правилу и имеющих одно имя, которое позволяет ссылаться на эту совокупность как на один объект, то есть мыслится как единое целое. Принадлежность произвольного элемента x множеству X обозначается как , а непринадлежность - .

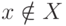Записывают множество X из элементов x, удовлетворяющих правилу P, в виде: X={x:P} или X={x|P}.

Если число элементов множества X конечно, то множество X называется конечным , в противном случае - бесконечным множеством и обозначаются, например, X (конечное) и Y (бесконечное), как X={x₁, x₂, ..., x_n} или и Y={y₁, y₂, ..., y_n,...} или .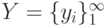

Пустое множество - это множество, формально вводимое в рассмотрение, но не содержащее ни одного элемента; обозначается пустое множество символом (это фиктивное множество играет роль нуля).

Универсальное множество ( универсум ) - это также формально вводимое множество, мыслимое как множество, содержащее все элементы всех множеств. Обозначается это множество 1 или I (оно играет роль единицы).

Подмножество множества X - это часть множества X, некоторая совокупность элементов из множества X . Подмножество множества само является множеством. Обозначают факт, что множество Y является подмножеством множества X, так: 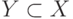или , если Y может полностью совпадать с X. Полное совпадение X и Y обозначается равенством вида X=Y.

Количество элементов конечного множества X называется мощностью этого множества и обозначается |X|. Для бесконечных множеств также рассматривается аналог этого понятия. Все множества, элементы которых можно "пересчитать" натуральными числами, имеют одну мощность, которая называется мощностью счетного множества; прочие именуются несчетными множествами.

Операциями, определенными над множествами, являются операции взятия подмножества множества, сравнения на совпадение (несовпадение), объединения, пересечения, дополнения, произведения множеств.

Объединение множеств X и Y - множество Z, полученное слиянием элементов X и Y, без дублирования совпадающих (одинаковых) элементов X и Y, например, получаемого добавлением к элементам множества X элементов множества Y, отличных от элементов X . Обозначается это объединение множеств как 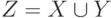. Это аналог операции суммирования.

Пересечением множеств X и Y называется множество Z, получаемое выделением всех совпадающих (одинаковых) элементов X и Y в отдельное множество Z . Обозначается 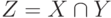и является аналогом произведения.

Дополнением ( до универсального множества ) множества X называется множество (обозначаемое как X или C(X) ), состоящее из всех элементов универсального множества 1, кроме элементов самого X . Дополнением (относительным) множества X до множества Y называется множество Z=X_Y (или Z=C_Y(X)), которое состоит из всех элементов Y, не вошедших в X.

Декартовым произведением множеств X и Y называется множество Z (обозначение ) всевозможных пар элементов вида (x,y), ,

Пример. Если X={a,b}, Y={a,c,d}, то 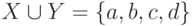, , 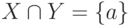, , 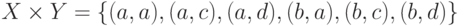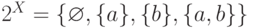C_Y(X)={c,d}, |X|=2.

Характеристическую функцию f множества X определим словесно (как и функцию Дирихле выше): если , то f(X)=1, иначе, то есть при 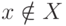, значение f(X)=0.

Пусть X, Y - некоторые непустые множества точек на числовой оси, то есть 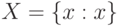, . Если каждому элементу однозначно поставлен в соответствие некоторый элемент , то говорят, что задана однозначная функция y=f(x) на множестве X со значениями во множестве Y . Множество X - это область определения функции, Y - область изменения функции f .Эти множества часто обозначают соответственно как D(f) и E(f). Переменная (независимая от другой переменной) x называется аргументом функции, переменная y (зависимая от x ) - значением функции (зависимой переменной),а правило, закон сопоставления каждому аргументу значения функции, - функцией. Функция - это зависимость переменной y от переменной x, если каждому значению x соответствует единственное значение y .

Определенная таким образом функция является числовой функцией , так как X и Y являются числовыми множествами, и .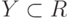

Иногда вместо термина "функция" используют термин "отображение" (множества X на множество Y или во множество Y ). Поэтому справедливо эквивалентное определение числовой функции: числовая функция есть отображение некоторого числового множества X (области определения функции) на другое числовое множество Y (являющееся множеством значений функции).

Обозначают отображения в общем случае в виде записи: .

В функциональной зависимости y=f(x), переменная x означает независимую переменную (то есть переменную, выбор значений которой из X независим), а y - зависимую переменную (то есть переменную, выбор значения которой из множества Y зависит от выбора x и правила f ), f - закон или правило, по которому выбирается y из множества Y .

Большинство закономерностей в природе и обществе описываются различными функциональными зависимостями, в которых одна величина (зависимая переменная) зависит от двух и более величин (независимых переменных). Функция может иметь много независимых переменных (зависимая переменная - одна, а каждое ее значение, соответствующее определенному набору независимых переменных, мы будем считать определяемой однозначно). Такие функции называются функциями нескольких переменных или функциями многих переменных.

Пример. Путь, проходимый телом при движении s=s(v,t), зависит от двух переменных: скорости тела v и времени движения t. Объем продукции первого типа, выпускаемой предприятием, равен x₁, второго типа - x₂, n - го типа - x_n. Стоимость единицы продукции первого типа - p₁ руб., второго типа - p₂, n -го типа - p_n. Тогда стоимость всей продукции будет определяться функцией n переменных: s=s(x₁,x₂,..., x_n) = p₁x₁ + p₂x₂ + ... + p_nx_n.

Итак, переменная z называется функцией переменных (x₁,x₂,...,x_n), если каждому допустимому набору значений переменных (x₁,x₂,...,x_n), или вектору x соответствует одно и только одно значение переменной z . Обозначается функция многих переменных как z=f(x₁,x₂,...,x_n) или z=f(x). Следовательно, каждому вектору x=(x₁,x₂,...,x_n) по некоторому закону f ставится в соответствие некоторое определенное число z.

Область определения D(f)={x : x=(x₁,x₂,...,x_n)} - множество векторов, для которых определена переменная z, область значений E(f)={z : z=f(x₁,x₂,...,x_n)} или множество значений, которые принимаются функцией f, когда вектор x принимает всевозможные значения из D(f)