Величины и их значения
Величины и их значения
Любое практическое применение числа ассоциируется (явно или неявно, интуитивно) с некоторым количеством, некоторой совокупностью предметов, объектов.
Пример. Число "четыре" может означать число стульев в комнате, число ножек у стула, число отличников в группе, число времен года и т.д. Все такие четырехэлементные совокупности можно отождествить, когда нас интересует лишь количество элементов в совокупности, и связать с элементом натурального ряда чисел "4".
Как люди в практической деятельности пришли к абстракции такого общего свойства совокупностей, как число?
Первоначально они не отделяли свойства числа от самих считаемых вещей. Счет, как правило, велся с помощью рук, пальцев, палочек, камешков и т.д. С дальнейшим развитием экономической жизни и общения совершенствовалась и техника счета. Общее свойство всех равночисленных совокупностей начинает выражаться через свойство какой-либо особенной совокупности. Дальнейшее развитие обмена между различными племенами, народами наталкивалось на определенное неудобство: эталон сравнения при счете у различных народов был различен, - у одних это были палочки, у других - ракушки, у третьих - зазубрины на дощечках. Поэтому в результате длительного исторического развития понятие числа освобождается от его конкретной общественной оболочки (палочек, камешков, зазубрин на доске и т.п.) и начинает выступать как абстракция - как число вообще, как натуральный ряд чисел.
В истории формирования понятия натурального числа можно выделить четыре основных этапа (по развитию техники счета):
- Установление равной численности различных совокупностей предметов.
- Выражение численности какой-то определенной совокупности предметов через ряд эквивалентных ей совокупностей.
- Определенная совокупность начинает уже выступать в качестве эталона количества.
- Общее свойство всех эквивалентных совокупностей выступает в "чистом" виде, как абстрактное понятие натурального числа.
Этот этап был объективно подготовлен длительной предшествующей практикой человечества.
"Чтобы считать, надо иметь не только предметы, но и обладать способностью отвлекаться при рассматривании этих предметов от всех прочих их свойств, кроме числа, а эта способность есть результат долгого, опирающегося на опыт, исторического развития" (Ф. Энгельс).
Далее математика отвлекается (абстрагируется) от конкретного количества, связанного с числами (от "числового содержания величин"), и вводятся дроби, отрицательные числа, операции над символами конкретных чисел и т.д.
Пример.Отрицательные числа позволили удобно отображать величину долга. Дроби позволили выделять части площадей.
Натуральными числами называют числа 1, 2, 3,... то есть целые положительные числа. Обозначают эту совокупность чисел буквой N. Эти числа были введены, например, для натурального счета, для перечисления и нумерации, каждое новое образовывалось добавлением к предыдущему единицы (новой палочки при счете палочками).
Совокупность всех целых чисел ..., -2, -1, 0, 1, 2, ... обозначают буквой Z. Эти числа были также введены ради практических нужд, например, для того чтобы было удобно работать с "долгами", налогами.
Рациональными числами называют все целые и дробные числа (как положительные, так и отрицательные), включая и нуль. Любое рациональное число представимо в виде дроби p/q, p - целое число, q - натуральное число. Рациональные числа могут быть представлены в виде конечных или бесконечных периодических дробей. Эти числа были введены, например, для работы с частями целого, для представления частей целого.
Совокупность рациональных чисел часто обозначают буквой Q.
Иррациональные числа - это числа, представимые бесконечными, но не периодическими десятичными дробями. Их совокупность обозначают часто буквой I. Эти числа введены, например, для нахождения сторон квадратов, равновеликих (равных по площади) другим фигурам.
Действительными (вещественными числами) называют совокупность иррациональных и рациональных чисел. Обозначают ее буквой R. Эти числа ввели для объединения всех ранее введенных чисел в одно целое, в более крупный числовой формализм.
Пример. Укажем, каким совокупностям чисел принадлежат числа
 ,
, 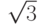 ,
,  ,
, 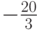 . Число
. Число  принадлежит совокупности
принадлежит совокупности  , а, следовательно, и совокупностям
, а, следовательно, и совокупностям  ,
,  ,
,  ; число
; число 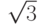 принадлежит совокупностям
принадлежит совокупностям  ,
,  ; число
; число  принадлежит совокупностям
принадлежит совокупностям  ,
,  ,
,  ,
,  ; число
; число 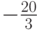 принадлежит совокупностям
принадлежит совокупностям  ,
,  .
.
Комплексное число - это число, представимое символически в виде суммы вида c=a+bi, где a, b - некоторые вещественные числа, а i - корень уравнения i2=-1. Величина 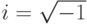 называется мнимой единицей . Число a - действительная составляющая комплексного числа c, а b - мнимая составляющая этого числа c. Совокупность комплексных чисел обозначается обычно буквой C и включает в себя совокупность R, а следовательно, и совокупности Q, I, N. Эти числа были введены, например, для того, чтобы можно было находить решения квадратных уравнений с отрицательными дискриминантами, когда решение таких уравнений стало необходимостью.
называется мнимой единицей . Число a - действительная составляющая комплексного числа c, а b - мнимая составляющая этого числа c. Совокупность комплексных чисел обозначается обычно буквой C и включает в себя совокупность R, а следовательно, и совокупности Q, I, N. Эти числа были введены, например, для того, чтобы можно было находить решения квадратных уравнений с отрицательными дискриминантами, когда решение таких уравнений стало необходимостью.
Постоянной ( константой ) называется величина, численное значение которой не изменяется (считается неизменным). Если для некоторой постоянной неважно ее значение, а важно лишь то, что она постоянная, то обычно эту постоянную в математике обозначают сокращением const (константа).
Переменной называется величина, принимающая различные числовые значения при различных условиях, в различных задачах. Для переменных используют буквенные или буквенно-цифровые обозначения. Кроме них, для переменных необходимо указывать и второй их атрибут - совокупность значений, которые может принимать данная переменная. Эта совокупность называется областью изменения переменной.
Пример. Переменная a для работы с длинами отрезков имеет область изменения [0;M], где M - любое конечное число.
Совокупность значений переменной с областью изменения от вещественного числа a включительно до вещественного числа b включительно называется отрезком ( замкнутым интервалом, промежутком ) и обозначается как [a;b]. Если одно из чисел a, b не включается в область изменения, то промежуток (интервал) называется полуоткрытым (или полузамкнутым) и обозначается как (a;b] или [a;b), а если оба эти числа не включаются, то промежуток называется открытым интервалом или просто интервалом и обозначается как (a;b).
Длиной промежутков [a;b], (a;b], [a;b), (a;b) назовем число, равное b-a . В математике есть два совершенно особых числа. Это, на самом деле, и не числа вовсе (в выше введенном понимании, то есть отождествляемые с конкретными определенными количествами), а некоторые математические абстракции, удобные обобщения "очень больших" положительных и "очень больших" отрицательных чисел. Эти "числа" обозначаются как  (положительная бесконечность) и
(положительная бесконечность) и  (отрицательная бесконечность) и играют очень важную роль в математике.
(отрицательная бесконечность) и играют очень важную роль в математике.
Пример.
Числа совокупности  можно определить как промежуток
можно определить как промежуток  . Если взять произвольную точку (число) из
. Если взять произвольную точку (число) из  , то
, то  - окрестностью точки
- окрестностью точки  будем называть открытый интервал длиной
будем называть открытый интервал длиной  с центром в точке
с центром в точке  , то есть промежуток
, то есть промежуток  ;
;  - радиус окрестности,
- радиус окрестности,  - центр окрестности. При этом предполагаем, часто неявно, что величина
- центр окрестности. При этом предполагаем, часто неявно, что величина  - достаточно малое число, так как понятие окрестности, в отличие от интервала, вводится именно для обозначения достаточно малой длины интервала с центром в точке
- достаточно малое число, так как понятие окрестности, в отличие от интервала, вводится именно для обозначения достаточно малой длины интервала с центром в точке  .
.
Пример.
Укажем промежутки, образующие  -окрестности чисел -2 ; 0 ;
-окрестности чисел -2 ; 0 ; 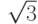 ; 10,5, если
; 10,5, если 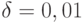 . Эти промежутки, соответственно, (-2,01; -1,99), (-0,01; 0,01),
. Эти промежутки, соответственно, (-2,01; -1,99), (-0,01; 0,01), 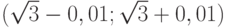 , (10,49;10,51).
, (10,49;10,51).
