Параллельные методы решения дифференциальных уравнений в частных производных
11.3.4. Организация волны вычислений
Представленные в пп. 11.3.1 – 11.3.3 алгоритмы определяют общую схему параллельных вычислений для метода сеток в многопроцессорных системах с распределенной памятью. Далее эта схема может быть конкретизирована реализацией практически всех вариантов методов, рассмотренных для систем с общей памятью (применение дополнительной памяти для схемы Гаусса – Якоби, чередование обработки полос и т.п.). Проработка таких вариантов не привносит каких-либо новых эффектов с точки зрения параллельных вычислений, и их разбор может использоваться как тема заданий для самостоятельных упражнений.
| Размер сетки | Последовательный метод Гаусса - Зейделя (алгоритм 11.1) | Параллельный алгоритм 11.8 | Параллельный алгоритм с волновой схемой расчета (см. п. 11.3.4) | |||||
|---|---|---|---|---|---|---|---|---|
| k | t | k | t | S | k | t | S | |
| 100 | 210 | 0,06 | 210 | 0,54 | 0,11 | 210 | 1,27 | 0,05 |
| 200 | 273 | 0,35 | 273 | 0,86 | 0,41 | 273 | 1,37 | 0,26 |
| 300 | 305 | 0,92 | 305 | 0,92 | 1,00 | 305 | 1,83 | 0,50 |
| 400 | 318 | 1,69 | 318 | 1,27 | 1,33 | 318 | 2,53 | 0,67 |
| 500 | 343 | 2,88 | 343 | 1,72 | 1,68 | 343 | 3,26 | 0,88 |
| 600 | 336 | 4,04 | 336 | 2,16 | 1,87 | 336 | 3,66 | 1,10 |
| 700 | 344 | 5,68 | 344 | 2,52 | 2,25 | 344 | 4,64 | 1,22 |
| 800 | 343 | 7,37 | 343 | 3,32 | 2,22 | 343 | 5,65 | 1,30 |
| 900 | 358 | 9,94 | 358 | 4,12 | 2,41 | 358 | 7,53 | 1,32 |
| 1000 | 351 | 11,87 | 351 | 4,43 | 2,68 | 351 | 8,10 | 1,46 |
| 2000 | 367 | 50,19 | 367 | 15,13 | 3,32 | 367 | 27,00 | 1,86 |
| 3000 | 364 | 113,17 | 364 | 37,96 | 2,98 | 364 | 55,76 | 2,03 |
( k – количество итераций, t – время (сек), S – ускорение )
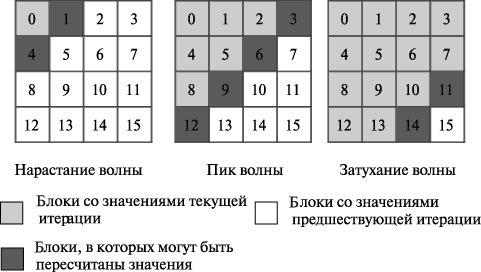
В завершение рассмотрим возможность организации параллельных вычислений, при которых обеспечивалось бы нахождение таких же решений задачи Дирихле, что и при использовании исходного последовательного метода Гаусса – Зейделя. Как отмечалось ранее, такой результат может быть получен за счет организации волновой схемы расчетов. Для образования волны вычислений представим логически каждую полосу узлов области расчетов в виде набора блоков (размер блоков можно положить, в частности, равным ширине полосы) и организуем обработку полос поблочно в последовательном порядке (см. рис. 11.12). Тогда для полного повторения действий последовательного алгоритма вычисления могут быть начаты только для первого блока первой полосы узлов; после того как этот блок будет обработан, для вычислений будут готовы уже два блока – блок 2 первой полосы и блок 1 второй полосы (для обработки блока полосы 2 необходимо передать граничную строку узлов первого блока полосы 1). После обработки указанных блоков к вычислениям будут готовы уже 3 блока, и мы получаем знакомый уже процесс волновой обработки данных (результаты экспериментов см. в табл. 11.4).
Интересный момент при организации подобной схемы параллельных вычислений может состоять в попытке совмещения операций пересылки граничных строк и действий по обработке блоков данных.
11.3.5. Блочная схема разделения данных
Ленточная схема разделения данных может быть естественным
образом обобщена на блочный способ представления сетки области
расчетов (см. рис. 11.9). При этом столь радикальное изменение
способа разбиения сетки практически не потребует каких-либо
существенных корректировок рассмотренной схемы параллельных
вычислений. Основной новый момент при блочном представлении
данных состоит в увеличении количества граничных строк на каждом
процессоре (для блока их количество становится равным 4), что
приводит, соответственно, к большему числу операций передачи
данных при обмене граничных строк. Сравнивая затраты на
организацию передачи граничных строк, можно отметить, что при
ленточной схеме для каждого процессора выполняется 4 операции
приема-передачи данных, в каждой из которых пересылаются (N+2)
значения. Для блочного же способа происходит 8 операций пересылки
и объем каждого сообщения равен  ( N – количество
внутренних узлов сетки, NP – число процессоров, размер всех
блоков предполагается одинаковым). Тем самым, блочная схема
представления области расчетов становится оправданной при большом
количестве узлов сетки, когда увеличение количества
коммуникационных операций приводит к снижению затрат на пересылку
данных в силу сокращения размеров передаваемых сообщений.
Результаты экспериментов при блочной схеме разделения данных
приведены в табл. 11.5.
( N – количество
внутренних узлов сетки, NP – число процессоров, размер всех
блоков предполагается одинаковым). Тем самым, блочная схема
представления области расчетов становится оправданной при большом
количестве узлов сетки, когда увеличение количества
коммуникационных операций приводит к снижению затрат на пересылку
данных в силу сокращения размеров передаваемых сообщений.
Результаты экспериментов при блочной схеме разделения данных
приведены в табл. 11.5.
| Размер сетки | Последовательный метод Гаусса - Зейделя (алгоритм 11.1) | Параллельный алгоритм с блочной схемой рассчета (см. п. 11.3.5) | Параллельный алгоритм 11.9 | |||||
|---|---|---|---|---|---|---|---|---|
| k | t | k | t | S | k | t | S | |
| 100 | 210 | 0,06 | 210 | 0,71 | 0,08 | 210 | 0,60 | 0,10 |
| 200 | 273 | 0,35 | 273 | 0,74 | 0,47 | 273 | 1,06 | 0,33 |
| 300 | 305 | 0,92 | 305 | 1,04 | 0,88 | 305 | 2,01 | 0,46 |
| 400 | 318 | 1,69 | 318 | 1,44 | 1,18 | 318 | 2,63 | 0,64 |
| 500 | 343 | 2,88 | 343 | 1,91 | 1,51 | 343 | 3,60 | 0,80 |
| 600 | 336 | 4,04 | 336 | 2,39 | 1,69 | 336 | 4,63 | 0,87 |
| 700 | 344 | 5,68 | 344 | 2,96 | 1,92 | 344 | 5,81 | 0,98 |
| 800 | 343 | 7,37 | 343 | 3,58 | 2,06 | 343 | 7,65 | 0,96 |
| 900 | 358 | 9,94 | 358 | 4,50 | 2,21 | 358 | 9,57 | 1,04 |
| 1000 | 351 | 11,87 | 351 | 4,90 | 2,42 | 351 | 11,16 | 1,06 |
| 2000 | 367 | 50,19 | 367 | 16,07 | 3,12 | 367 | 39,49 | 1,27 |
| 3000 | 364 | 113,17 | 364 | 39,25 | 2,88 | 364 | 85,72 | 1,32 |
( k – количество итераций, t – время (сек), S – ускорение )
При блочном представлении сетки может быть реализован также и
волновой метод выполнения расчетов (см. рис. 11.13). Пусть
процессоры образуют прямоугольную решетку размером 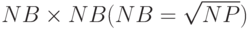 и процессоры пронумерованы от 0 слева направо по строкам
решетки.
и процессоры пронумерованы от 0 слева направо по строкам
решетки.
Общая схема параллельных вычислений в этом случае имеет вид:
Алгоритм 11.9. Блочная схема разделения данных
// Алгоритм 11.9
// схема Гаусса-Зейделя, блочное разделение данных
// действия, выполняемые на каждом процессоре
do {
// получение граничных узлов
if ( ProcNum / NB != 0 ) { // строка не нулевая
// получение данных от верхнего процессора
Receive(u[0][*],M+2,TopProc); // верхняя строка
Receive(dmax,1,TopProc); // погрешность
}
if ( ProcNum % NB != 0 ) { // столбец не нулевой
// получение данных от левого процессора
Receive(u[*][0],M+2,LeftProc); // левый столбец
Receive(dm,1,LeftProc); // погрешность
if ( dm > dmax ) dmax = dm;
}
// <обработка блока с оценкой погрешности dmax>
// пересылка граничных узлов
if ( ProcNum / NB != NB-1 ) { // строка решетки не последняя
// пересылка данных нижнему процессору
Send(u[M+1][*],M+2,DownProc); // нижняя строка
Send(dmax,1,DownProc); // погрешность
}
if ( ProcNum % NB != NB-1 ) { // столбец решетки не последний
// пересылка данных правому процессору
Send(u[*][M+1],M+2,RightProc); // правый столбец
Send(dmax,1, RightProc); // погрешность
}
// синхронизация и рассылка погрешности dmax
Broadcast(dmax,NP-1);
} while ( dmax > eps ); // eps — точность решения
11.9.
При реализации алгоритма необходимо обеспечить, чтобы в начальный момент времени все процессоры (кроме процессора с нулевым номером) оказались в состоянии передачи своих граничных узлов (верхней строки и левого столбца). Вычисления должен начинать процессор с левым верхним блоком, после завершения обработки которого обновленные значения правого столбца и нижней строки блока нужно переправить правому и нижнему процессорам решетки соответственно. Данные действия обеспечат снятие блокировки процессоров второй диагонали процессорной решетки (ситуация слева на рис. 11.13) и т.д.
Анализ эффективности организации волновых вычислений в системах с распределенной памятью (см. табл. 11.5) показывает значительное снижение полезной вычислительной нагрузки для процессоров, которые занимаются обработкой данных только в моменты, когда их блоки попадают во фронт волны вычислений. При этом балансировка (перераспределение) нагрузки является крайне затруднительной, поскольку связана с пересылкой между процессорами блоков данных большого объема. Возможный интересный способ улучшения ситуации состоит в организации множественной волны вычислений, в соответствии с которой процессоры после отработки волны текущей итерации расчетов могут приступить к выполнению волны следующей итерации метода сеток. Так, например, процессор 0 (см. рис. 11.13), передав после обработки своего блока граничные данные и запустив тем самым вычисления на процессорах 1 и 4, оказывается готовым к исполнению следующей итерации метода Гаусса – Зейделя. После обработки блоков первой (процессоры 1 и 4) и второй (процессор 0) волн к вычислениям окажутся готовыми следующие группы процессоров (для первой волны — процессоры 2, 5 и 8, для второй — процессоры 1 и 4). Кроме того, процессор 0 опять окажется готовым к запуску очередной волны обработки данных. После выполнения NB подобных шагов в обработке будет находиться одновременно NB итераций и все процессоры окажутся задействованными. Подобная схема организации расчетов позволяет рассматривать имеющуюся процессорную решетку как вычислительный конвейер поэтапного выполнения итераций метода сеток. Остановка конвейера может осуществляться, как и ранее, по максимальной погрешности вычислений (проверку условия остановки следует начинать только при достижении полной загрузки конвейера после запуска NB итераций расчетов). Необходимо отметить также, что получаемое после выполнения условия остановки решение задачи Дирихле будет содержать значения узлов сетки от разных итераций метода и не будет, тем самым, совпадать с решением, получаемым при помощи исходного последовательного алгоритма.
11.3.6. Оценка трудоемкости операций передачи данных
Время выполнения коммуникационных операций значительно превышает длительность вычислительных команд. Оценка трудоемкости операций приема-передачи может быть осуществлена с использованием двух основных характеристик сети передачи: латентности ( latency ), определяющей время подготовки данных к передаче по сети, и пропускной способности сети ( bandwidth ), задающей объем передаваемых по сети за 1 секунду данных, – более полное изложение вопроса содержится в "Оценка коммуникационной трудоемкости параллельных алгоритмов" .
Пропускная способность наиболее распространенной на данный момент сети Fast Ethernet – 100 Mбит/с, для более современной сети Gigabit Ethernet – 1000 Мбит/с. В то же время скорость передачи данных в системах с общей памятью обычно составляет сотни и тысячи миллионов байт в секунду. Тем самым, использование систем с распределенной памятью приводит к снижению скорости передачи данных не менее чем в 100 раз.
Еще хуже дело обстоит с латентностью. Для сети Fast Ethernet эта характеристика имеет значение порядка 150 мкс, для сети Gigabit Ethernet – около 100 мкс. Для современных компьютеров с тактовой частотой свыше 2 ГГц различие в производительности достигает не менее чем 10000 – 100000 раз. При указанных характеристиках вычислительной системы для достижения 90% эффективности в рассматриваемом примере решения задачи Дирихле (т.е. чтобы в ходе расчетов обработка данных занимала не менее 90% времени от общей длительности вычислений и только 10% времени тратилось бы на операции передачи данных ) размер блоков вычислительной сетки должен быть не менее N=7500 узлов по вертикали и горизонтали (объем вычислений в блоке составляет 5N2 операций с плавающей запятой).
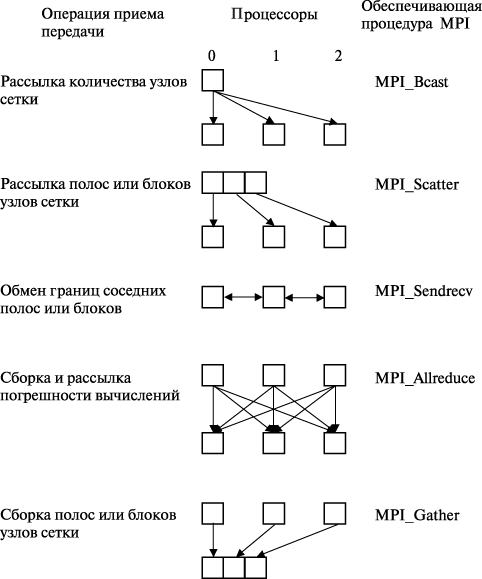
Как результат, можно заключить, что эффективность параллельных вычислений при использовании распределенной памяти определяется в основном интенсивностью и видом выполняемых коммуникационных операций при взаимодействии процессоров. Необходимый при этом анализ параллельных методов и программ может быть выполнен значительно быстрее за счет выделения типовых операций передачи данных – см. "Оценка коммуникационной трудоемкости параллельных алгоритмов" . Так, например, в рассматриваемом учебном примере решения задачи Дирихле практически все пересылки значений сводятся к стандартным коммуникационным действиям, имеющим адекватную поддержку в стандарте MPI (см. рис. 11.14):
- рассылка количества узлов сетки всем процессорам – типовая операция передачи данных от одного процессора всем процессорам сети (функция MPI_Bcast );
- рассылка полос или блоков узлов сетки всем процессорам – типовая операция передачи разных данных от одного процессора всем процессорам сети (функция MPI_Scatter );
- обмен граничных строк или столбцов сетки между соседними процессорами – типовая операция передачи данных между соседними процессорами сети (функция MPI_Sendrecv );
- сборка и рассылка погрешности вычислений всем процессорам – типовая операция передачи данных от всех процессоров всем процессорам сети (функция MPI_Allreduce );
- сборка на одном процессоре решения задачи (всех полос или блоков сетки) – типовая операция передачи данных от всех процессоров сети одному процессору (функция MPI_Gather ).