Параллельные методы решения дифференциальных уравнений в частных производных

11.3. Организация параллельных вычислений для систем с распределенной памятью

Использование процессоров с распределенной памятью является другим общим способом построения многопроцессорных вычислительных систем. Актуальность их становится все более высокой в последнее время в связи с широким развитием высокопроизводительных кластерных вычислительных систем (см. "Принципы построения параллельных вычислительных систем" ).

Многие проблемы параллельного программирования (состязание вычислений, тупики, сериализация) являются общими для систем с общей и распределенной памятью. Основной момент, который отличает параллельные вычисления с распределенной памятью, состоит в том, что взаимодействие параллельных участков программы на разных процессорах может быть обеспечено только при помощи передачи сообщений ( message passing ).

Следует отметить, что вычислительный узел системы с распределенной памятью является, как правило, более сложным вычислительным устройством, чем процессор в многопроцессорной системе с общей памятью. Для учета этих различий в дальнейшем процессор с распределенной памятью будет именоваться вычислительным сервером (сервером может быть, в частности, многопроцессорная система с общей памятью). При проведении всех ниже рассмотренных экспериментов использовались 4 компьютера с процессорами Pentium IV, 1300 Mhz, 256 RAM, 100 Mbit Fast Ethernet.

11.3.1. Общие принципы распределения данных

Первая проблема, которую приходится решать при организации параллельных вычислений на системах с распределенной памятью, обычно состоит в выборе способа разделения обрабатываемых данных между вычислительными серверами. Успешность такого разделения определяется достигнутой степенью локализации вычислений на серверах (в силу больших временных задержек при передаче сообщений интенсивность взаимодействия серверов должна быть минимальной).

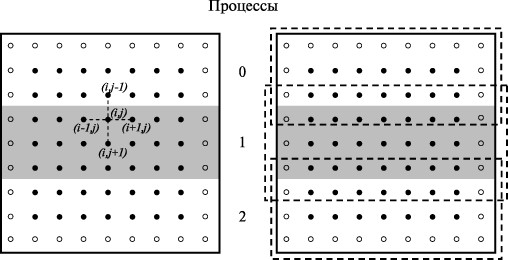
Рис. 11.10. Ленточное разделение области расчетов между процессорами (кружки представляют граничные узлы сетки)

В рассматриваемом учебном примере по решению задачи Дирихле возможны два различных способа разделения данных – одномерная или ленточная схема (см. рис. 11.10) и двумерное или блочное разбиение (см. рис. 11.9) вычислительной сетки. Дальнейшее изложение учебного материала будет проводиться на примере первого подхода; блочная схема будет рассмотрена позднее в более кратком виде.

При ленточном разбиении область расчетов делится на горизонтальные или вертикальные полосы (не уменьшая общности, далее будем рассматривать только горизонтальные полосы). Число полос определяется количеством процессоров, размер полос обычно является одинаковым, узлы горизонтальных границ (первая и последняя строки) включаются в первую и последнюю полосы соответственно. Полосы для обработки распределяются между процессорами.

Основной момент при организации вычислений с подобным разделением данных состоит в том, что на процессор, выполняющий обработку какой-либо полосы, должны быть продублированы граничные строки предшествующей и следующей полос вычислительной сетки (получаемые в результате расширенные полосы показаны на рис. 11.10 справа пунктирными рамками). Продублированные граничные строки полос используются только при проведении расчетов, пересчет же этих строк происходит в полосах своего исходного месторасположения. Тем самым, дублирование граничных строк должно осуществляться перед началом выполнения каждой очередной итерации метода сеток.

11.3.2. Обмен информацией между процессорами

Параллельный вариант метода сеток при ленточном разделении данных состоит в обработке полос на всех имеющихся серверах одновременно в соответствии со следующей схемой работы:

Алгоритм 11.8. Параллельный алгоритм, реализующий метод сеток при ленточном разделении данных

// Алгоритм 11.8
// схема Гаусса-Зейделя, ленточное разделение данных
// действия, выполняемые на каждом процессоре
do {
  // <обмен граничных строк полос с соседями>
  // <обработка полосы>
  // <вычисление общей погрешности вычислений dmax>}
 while ( dmax > eps ); // eps — точность решения

Для конкретизации представленных в алгоритме действий введем обозначения:

• ProcNum – номер процессора, на котором выполняются описываемые действия,
• PrevProc, NextProc – номера соседних процессоров, содержащих предшествующую и следующую полосы,
• NP – количество процессоров,
• M – количество строк в полосе (без учета продублированных граничных строк),
• N – количество внутренних узлов в строке сетки (т.е. всего в строке N+2 узла).

При нумерации строк полосы будем считать, что строки 0 и M+1 есть продублированные из соседних полос граничные строки, а строки собственной полосы процессора имеют номера от 1 до M.

Рис. 11.11. Схема передачи граничных строк между соседними процессорами

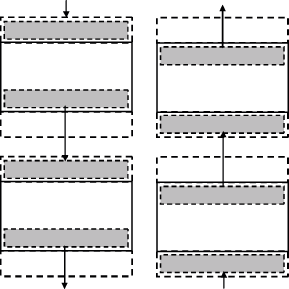
Процедура обмена граничных строк между соседними процессорами может быть разделена на две последовательные операции, во время первой из которых каждый процессор передает свою нижнюю граничную строку следующему процессору и принимает такую же строку от предыдущего процессора (см. рис. 11.11). Вторая часть передачи строк выполняется в обратном направлении: процессоры передают свои верхние граничные строки своим предыдущим соседям и принимают переданные строки от следующих процессоров.

Выполнение подобных операций передачи данных в общем виде может быть представлено следующим образом (для краткости рассмотрим только первую часть процедуры обмена):

// передача нижней граничной строки следующему 
// процессору и прием передаваемой строки от 
// предыдущего процессора
if ( ProcNum != NP-1 ) Send(u[M][*],N+2,NextProc);
if ( ProcNum != 0 ) Receive(u[0][*],N+2,PrevProc);

(для записи процедур приема-передачи используется близкий к стандарту MPI (см. "Параллельное программирование на основе MPI" ) формат, где первый и второй параметры представляют пересылаемые данные и их объем, а третий параметр определяет адресата (для операции Send ) или источник (для операции Receive ) пересылки данных).

Для передачи данных могут быть задействованы два различных механизма. При первом из них выполнение программ, инициировавших операцию передачи, приостанавливается до полного завершения всех действий по пересылке данных (т.е. до момента получения процессором-адресатом всех передаваемых ему данных). Операции приема-передачи, реализуемые подобным образом, обычно называются синхронными или блокирующими. Иной подход – асинхронная или неблокирующая передача — может состоять в том, что операции приема-передачи только инициируют процесс пересылки и на этом завершают свое выполнение. В результате программы, не дожидаясь завершения длительных коммуникационных операций, могут продолжать свои вычислительные действия, проверяя по мере необходимости готовность передаваемых данных. Оба эти варианта операций передачи широко используются при организации параллельных вычислений и имеют свои достоинства и свои недостатки. Синхронные процедуры передачи, как правило, более просты для применения и более надежны; неблокирующие операции могут позволить совместить процессы передачи данных и вычислений, но обычно приводят к повышению сложности программирования. С учетом вышесказанного во всех последующих примерах для организации пересылки данных будут использоваться операции приема-передачи блокирующего типа.

Приведенная выше последовательность блокирующих операций приема-передачи данных (вначале Send, затем Receive ) приводит к строго последовательной схеме выполнения процесса пересылок строк, т.к. все процессоры одновременно обращаются к операции Send и переходят в режим ожидания. Первым процессором, который окажется готовым к приему пересылаемых данных, будет сервер с номером NP-1. В результате процессор NP-2 выполнит операцию передачи своей граничной строки и перейдет к приему строки от процессора NP-3 и т.д. Общее количество повторений таких операций равно NP-1. Аналогично происходит выполнение и второй части процедуры пересылки граничных строк перед началом обработки строк (см. рис. 11.11).

Последовательный характер рассмотренных операций пересылок данных определяется выбранным способом очередности выполнения. Изменим этот порядок очередности при помощи чередования приема и передачи для процессоров с четными и нечетными номерами.

// передача нижней граничной строки следующему
// процессору и прием передаваемой строки от 
// предыдущего процессора
if ( ProcNum % 2 == 1 ) { //  нечетный процессор
  if ( ProcNum != NP-1 ) Send(u[M][*],N+2,NextProc);
  if ( ProcNum != 0 ) Receive(u[0][*],N+2,PrevProc);
}
else { //  процессор с четным номером
  if ( ProcNum != 0 ) Receive(u[0][*],N+2,PrevProc);
  if ( ProcNum != NP-1 ) Send(u[M][*],N+2,NextProc);
}

Данный прием позволяет выполнить все необходимые операции передачи всего за два последовательных шага. На первом шаге все процессоры с нечетными номерами отправляют данные, а процессоры с четными номерами осуществляют прием этих данных. На втором шаге роли процессоров меняются – четные процессоры выполняют Send, нечетные процессоры исполняют операцию приема Receive.

Рассмотренные последовательности операций приема-передачи для взаимодействия соседних процессоров широко используются в практике параллельных вычислений. Как результат, во многих базовых библиотеках параллельных программ имеются процедуры для поддержки подобных действий. Так, в стандарте MPI (см. лекцию 5 ) предусмотрена операция Sendrecv, с использованием которой предыдущий фрагмент программного кода может быть записан более кратко:

// передача нижней граничной строки следующему
// процессору и прием передаваемой строки от
// предыдущего процессора
Sendrecv(u[M][*],N+2,NextProc,u[0][*],N+2,PrevProc);

Реализация подобной объединенной функции Sendrecv обычно осуществляется таким образом, чтобы обеспечить и корректную работу на крайних процессорах, когда не нужно выполнять одну из операций передачи или приема, и организацию чередования процедур передачи на процессорах для ухода от тупиковых ситуаций, и возможности параллельного выполнения всех необходимых пересылок данных.

11.3.3. Коллективные операции обмена информацией

Для завершения круга вопросов, связанных с параллельной реализацией метода сеток на системах с распределенной памятью, осталось рассмотреть способы вычисления общей для всех процессоров погрешности вычислений. Возможный очевидный подход состоит в передаче всех локальных оценок погрешности, полученных на отдельных полосах сетки, на один какой-либо процессор, вычислении на нем максимального значения и последующей рассылке полученного значения всем процессорам системы. Однако такая схема является крайне неэффективной – количество необходимых операций передачи данных определяется числом процессоров и выполнение этих операций может происходить только в последовательном режиме. Между тем, как показывает анализ требуемых коммуникационных действий, выполнение операций сборки и рассылки данных может быть реализовано с использованием рассмотренной в п. 2.5.2 каскадной схемы обработки данных. На самом деле, получение максимального значения локальных погрешностей, вычисленных на каждом процессоре, может быть обеспечено, например, путем предварительного нахождения максимальных значений для отдельных пар процессоров (такие вычисления могут выполняться параллельно), затем может быть снова осуществлен попарный поиск максимума среди полученных результатов и т.д. Всего, как полагается по каскадной схеме, необходимо выполнить log₂NP параллельных итераций для получения конечного значения ( NP – количество процессоров).

С учетом возможности применения каскадной схемы для выполнения коллективных операций передачи данных большинство базовых библиотек параллельных программ содержит процедуры для поддержки подобных действий. Так, в стандарте MPI (см. "Параллельное программирование на основе MPI" ) предусмотрены операции:

• Reduce(dm,dmax,op,proc) – процедура сборки на процессоре proc итогового результата dmax среди локальных на каждом процессоре значений dm с применением операции op ;
• Broadcast(dmax,proc) – процедура рассылки с процессора proc значения dmax всем имеющимся процессорам системы.

С учетом перечисленных процедур общая схема вычислений на каждом процессоре может быть представлена в следующем виде:

// Алгоритм 11.8 – уточненный вариант
// схема Гаусса-Зейделя, ленточное разделение данных
// действия, выполняемые на каждом процессоре
do {
  // обмен граничных строк полос с соседями
  Sendrecv(u[M][*],N+2,NextProc,u[0][*],N+2,PrevProc);
  Sendrecv(u[1][*],N+2,PrevProc,u[M+1][*],N+2,NextProc);
  // <обработка полосы с оценкой погрешности dm>
  // вычисление общей погрешности вычислений dmax
  Reduce(dm,dmax,MAX,0);
  Broadcast(dmax,0);
} while ( dmax > eps ); // eps — точность решения

(в приведенном алгоритме переменная dm представляет собой локальную погрешность вычислений на отдельном процессоре, а параметр MAX задает операцию поиска максимального значения для операции сборки). Следует отметить, что в составе MPI имеется процедура Allreduce, которая совмещает действия редукции и рассылки данных. Результаты экспериментов для данного варианта параллельных вычислений для метода Гаусса – Зейделя приведены в рис. 11.4.