Параллельные методы решения дифференциальных уравнений в частных производных
11.2.6. Волновые схемы параллельных вычислений
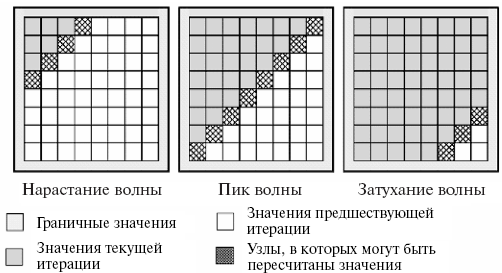
Рассмотрим теперь возможность построения параллельного алгоритма, который выполнял бы только те вычислительные действия, что и последовательный метод (может быть только в несколько ином порядке) и, как результат, обеспечивал бы получение точно таких же решений исходной вычислительной задачи. Как уже было отмечено выше, в последовательном алгоритме каждое очередное k -е приближение значения ui,j вычисляется по последнему k -му приближению значений ui-1,j и ui,j-1 и предпоследнему (k-1) -му приближению значений ui+1,j и ui,j+1. Таким образом, при требовании совпадения результатов вычислений последовательных и параллельных вычислительных схем в начале каждой итерации метода только одно значение u11 может быть пересчитано (возможности для распараллеливания нет). Но далее после пересчета u11 вычисления могут выполняться уже в двух узлах сетки u12 и u21 (в этих узлах выполняются условия последовательной схемы), затем после пересчета узлов u12 и u21 — в узлах u13, u22 и u31 и т.д. Обобщая сказанное, можно увидеть, что выполнение итерации метода сеток можно разбить на последовательность шагов, на каждом из которых к вычислениям окажутся подготовленными узлы вспомогательной диагонали сетки с номером, определяемым номером этапа – см. рис. 11.8. Получаемая в результате вычислительная схема получила наименование волны или фронта вычислений, а алгоритмы, построенные на ее основе, — методов волновой обработки данных ( wavefront или hyperplane methods ). Следует отметить, что в нашем случае размер волны (степень возможного параллелизма) динамически изменяется в ходе вычислений – волна нарастает до своего пика, а затем затухает при приближении к правому нижнему узлу сетки.
Возможная схема параллельного метода, основанного на эффекте волны вычислений, может быть представлена в следующей форме.
Алгоритм 11.5. Параллельный алгоритм, реализующий волновую схему вычислений
// Алгоритм 11.5
omp_lock_t dmax_lock;
omp_init_lock(dmax_lock);
do {
dmax = 0; // максимальное изменение значений u
// нарастание волны (nx – размер волны)
for ( nx=1; nx<N+1; nx++ ) {
dm[nx] = 0;
#pragma omp parallel for shared(u,N,nx,dm) private(i,j,temp,d)
for ( i=1; i<nx+1; i++ ) {
j = nx + 1 – i;
temp = u[i][j];
u[i][j] = 0.25*(u[i-1][j]+u[i+1][j]+
u[i][j-1]+u[i][j+1]–h*h*f[i][j]);
d = fabs(temp-u[i][j])
if ( dm[i] < d ) dm[i] = d;
} // конец параллельной области
}
// затухание волны
for ( nx=N-1; nx>0; nx-- ) {
#pragma omp parallel for shared(u,N,nx,dm) private(i,j,temp,d)
for ( i=N-nx+1; i<N+1; i++ ) {
j = 2*N - nx – I + 1;
temp = u[i][j];
u[i][j] = 0.25*(u[i-1][j]+u[i+1][j]+
u[i][j-1]+u[i][j+1]–h*h*f[i][j]);
d = fabs(temp-u[i][j])
if ( dm[i] < d ) dm[i] = d;
} // конец параллельной области
}
#pragma omp parallel for shared(nx,dm,dmax) private(i)
for ( i=1; i<nx+1; i++ ) {
omp_set_lock(dmax_lock);
if ( dmax < dm[i] ) dmax = dm[i];
omp_unset_lock(dmax_lock);
} // конец параллельной области
} while ( dmax > eps );
11.5.
При разработке алгоритма, реализующего волновую схему вычислений, оценку погрешности решения можно осуществлять для каждой строки в отдельности (массив значений dm ). Этот массив является общим для всех выполняемых потоков, однако синхронизации доступа к элементам не требуется, так как потоки используют всегда разные элементы массива (фронт волны вычислений содержит только по одному узлу строк сетки).
После обработки всех элементов волны в составе массива dm находится максимальная погрешность выполненной итерации вычислений. Однако именно эта последняя часть расчетов может оказаться наиболее неэффективной из-за высоких дополнительных затрат на синхронизацию. Улучшение ситуации, как и ранее, может быть достигнуто за счет увеличения размера последовательных участков и сокращения, тем самым, количества необходимых взаимодействий параллельных участков вычислений. Возможный вариант реализации такого подхода может состоять в следующем:
chunk = 200; // размер последовательного участка
#pragma omp parallel for shared(n,dm,dmax) private(i,d)
for ( i=1; i<nx+1; i+=chunk ) {
d = 0;
for ( j=i; j<i+chunk; j++ )
if ( d < dm[j] ) d = dm[j];
omp_set_lock(dmax_lock);
if ( dmax < d ) dmax = d;
omp_unset_lock(dmax_lock);
} // конец параллельной области( k – количество итераций, t – время (сек), S – ускорение )
Подобный прием укрупнения последовательных участков вычислений для снижения затрат на синхронизацию именуется фрагментированием ( chunking ). Результаты экспериментов для данного варианта параллельных вычислений приведены в табл. 11.3.
Следует обратить внимание еще на один момент при анализе эффективности разработанного параллельного алгоритма. Фронт волны вычислений плохо соответствует правилам использования кэша — быстродействующей дополнительной памяти компьютера, используемой для хранения копии данных, хранимых в оперативной памяти. Применение кэша может существенно повысить (в десятки раз) быстродействие вычислений. Размещение данных в кэше может происходить или предварительно (при использовании тех или иных алгоритмов предсказания потребности в данных), или в момент извлечения значений из основной оперативной памяти. При этом подкачка данных в кэш осуществляется не одиночными значениями, а небольшими группами – строками кэша ( cache line ). Загрузка значений в строку кэша осуществляется из последовательных элементов памяти; типовые размеры строки кэша обычно равны 32, 64, 128, 256 байтам (дополнительная информация по организации памяти может быть получена, например, в [ [ 16 ] ]). Как результат, эффект наличия кэша будет наблюдаться, если выполняемые вычисления используют одни и те же данные многократно ( локальность обработки данных) и осуществляют доступ к элементам памяти с последовательно возрастающими адресами ( последовательность доступа ).
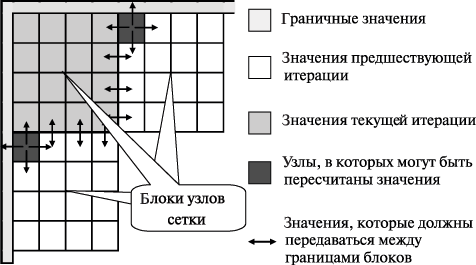
В исследуемом нами алгоритме размещение данных в памяти осуществляется по строкам, а фронт волны вычислений располагается по диагонали сетки, и это приводит к низкой эффективности использования кэша. Возможный способ улучшения ситуации – опять же укрупнение вычислительных операций и рассмотрение в качестве распределяемых между процессорами действий процедуры обработки некоторой прямоугольной подобласти ( блока ) сетки области расчетов – (см. рис. 11.9).
Порождаемый на основе такого подхода метод вычислений в самом общем виде может быть описан следующим образом (блоки образуют в области расчетов прямоугольную решетку размера NBxNB ):