Параллельные методы решения дифференциальных уравнений в частных производных

11.2.3. Возможность неоднозначности вычислений в параллельных программах

Последний рассмотренный вариант организации параллельных вычислений для метода сеток обеспечивает практически максимально возможное ускорение выполняемых расчетов – так, в экспериментах данное ускорение достигало величины 5,9 при использовании четырехпроцессорного вычислительного сервера. Вместе с этим необходимо отметить, что разработанная вычислительная схема расчетов имеет важную принципиальную особенность: порождаемая при вычислениях последовательность обработки данных может различаться при разных запусках программы даже при одних и тех же исходных параметрах решаемой задачи. Данный эффект может проявляться в силу изменения каких-либо условий выполнения программы (вычислительной нагрузки, алгоритмов синхронизации потоков и т.п.), что может повлиять на временные соотношения между потоками (см. рис. 11.5). Взаиморасположение потоков по области расчетов может быть различным: одни потоки могут опережать другие и, наоборот, часть потоков могут отставать (при этом характер взаиморасположения может меняться в ходе вычислений). Подобное поведение параллельных участков программы обычно именуется состязанием потоков ( race condition ) и отражает важный принцип параллельного программирования – временная динамика выполнения параллельных потоков не должна учитываться при разработке параллельных алгоритмов и программ.

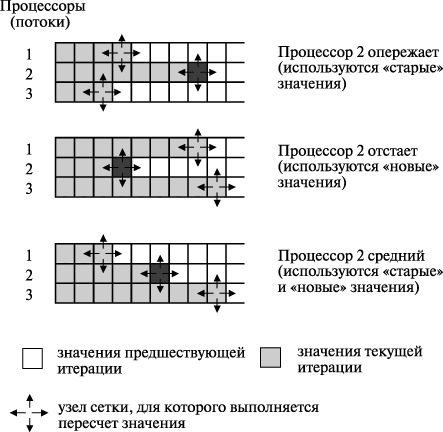
Рис. 11.5. Возможные различные варианты взаиморасположения параллельных потоков (состязание потоков)

В рассматриваемом примере при вычислении нового значения u_ij в зависимости от условий выполнения могут использоваться разные (от предыдущей или текущей итераций) оценки соседних значений по вертикали. Тем самым, количество итераций метода до выполнения условия остановки и, самое главное, конечное решение задачи могут различаться при повторных запусках программы. Получаемые оценки величин u_ij. будут соответствовать точному решению задачи в пределах задаваемой точности, но, тем не менее, могут быть различными. Применение вычислений такого типа для сеточных алгоритмов получило наименование метода хаотической релаксации ( chaotic relaxation ).

11.2.4. Проблема взаимоблокировки

Возможный подход для получения однозначных результатов (уход от состязания потоков) может состоять в ограничении доступа к узлам сетки, которые обрабатываются в параллельных потоках программы. Для этого можно ввести набор замков row_lock[N], который позволит потокам закрывать доступ к "своим" строкам сетки.

// поток обрабатывает i строку сетки
omp_set_lock(row_lock[i]);
omp_set_lock(row_lock[i+1]);
omp_set_lock(row_lock[i-1]);
// обработка i строки сетки
omp_unset_lock(row_lock[i]);
omp_unset_lock(row_lock[i+1]);
omp_unset_lock(row_lock[i-1]);

Закрыв доступ к своим данным, параллельный поток уже не будет зависеть от динамики выполнения других параллельных участков программы. Результат вычислений потока однозначно определяется значениями данных в момент начала расчетов.

Данный подход позволяет продемонстрировать еще одну проблему, которая может возникать в ходе параллельных вычислений. Эта проблема состоит в том, что при организации доступа к множественным общим переменным может появляться конфликт между параллельными потоками и этот конфликт не может быть разрешен успешно. Так, в приведенном фрагменте программного кода при обработке потоками двух последовательных строк (например, строк 1 и 2) может сложиться ситуация, когда потоки блокируют сначала строки 1 и 2 и только затем переходят к блокировке оставшихся строк (см. рис. 11.6). В этом случае доступ к необходимым строкам не может быть обеспечен ни для одного потока – возникает неразрешимая ситуация, обычно именуемая тупиком. Как можно показать, необходимым условием тупика является наличие цикла в графе распределения и запросов ресурсов. В рассматриваемом примере уход от цикла может состоять в строго последовательной схеме блокировки строк потока.

// поток обрабатывает i строку сетки
omp_set_lock(row_lock[i+1]);
omp_set_lock(row_lock[i]);
omp_set_lock(row_lock[i-1]);
// <обработка i строки сетки>
omp_unset_lock(row_lock[i+1]);
omp_unset_lock(row_lock[i]);
omp_unset_lock(row_lock[i-1]);

(следует отметить, что и эта схема блокировки строк может оказаться тупиковой, если рассматривать модифицированную задачу Дирихле, в которой горизонтальные границы являются "склеенными").

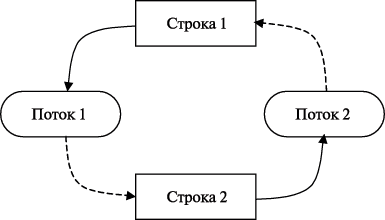
Рис. 11.6. Ситуация тупика при доступе к строкам сетки (поток 1 владеет строкой 1 и запрашивает строку 2, поток 2 владеет строкой 2 и запрашивает строку 1)

11.2.5. Исключение неоднозначности вычислений

Подход, рассмотренный в п. 11.2.4, уменьшает эффект состязания потоков, но не гарантирует единственности решения при повторении вычислений. Для достижения однозначности необходимо использование дополнительных вычислительных схем.

Возможный и широко применяемый в практике расчетов способ состоит в разделении места хранения результатов вычислений на предыдущей и текущей итерациях метода сеток. Схема такого подхода может быть представлена в следующем общем виде:

Алгоритм 11.4. Параллельная реализация сеточного метода Гаусса – Якоби

// Алгоритм 11.4
omp_lock_t dmax_lock;
omp_init_lock(dmax_lock);
do {
  dmax = 0; // максимальное изменение значений u
#pragma omp parallel for shared(u,un,N,dmax) private(i,temp,d,dm)
  for ( i=1; i<N+1; i++ ) {
    dm = 0;
    for ( j=1; j<N+1; j++ ) {
      temp = u[i][j];
      un[i][j] = 0.25*(u[i-1][j]+u[i+1][j]+
                 u[i][j-1]+u[i][j+1]–h*h*f[i][j]);
      d = fabs(temp-un[i][j])
      if ( dm < d ) dm = d;
    }
    omp_set_lock(dmax_lock);
      if ( dmax < dm ) dmax = dm;
    omp_unset_lock(dmax_lock);
    } 
  } // конец параллельной области
  for ( i=1; i<N+1; i++ ) // обновление данных
    for ( j=1; j<N+1; j++ ) 
      u[i][j] = un[i][j];
} while ( dmax > eps );

Как следует из приведенного алгоритма, результаты предыдущей итерации запоминаются в массиве u, новые вычисления значения запоминаются в дополнительном массиве un. Как результат, независимо от порядка выполнения вычислений для проведения расчетов всегда используются значения величин u_ij от предыдущей итерации метода. Такая схема реализации сеточных алгоритмов обычно именуется методом Гаусса – Якоби. Этот метод гарантирует однозначность результатов независимо от способа распараллеливания, но требует использования большого дополнительного объема памяти и обладает меньшей (по сравнению с алгоритмом Гаусса – Зейделя ) скоростью сходимости. Результаты расчетов с последовательным и параллельным вариантами метода приведены в табл. 11.2.

( k – количество итераций, t – время (сек), S – ускорение )

Рис. 11.7. Схема чередования обработки четных и нечетных строк

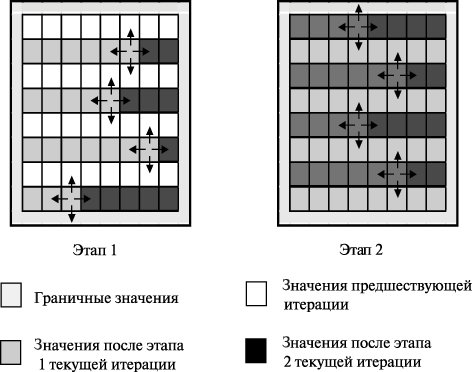
Иной возможный подход для устранения взаимозависимости параллельных потоков состоит в применении схемы чередования обработки четных и нечетных строк ( red/black row alternation scheme ), когда выполнение итерации метода сеток подразделяется на два последовательных этапа, на первом из которых обрабатываются строки только с четными номерами, а затем на втором этапе — строки с нечетными номерами (см. рис. 11.7). Данная схема может быть обобщена на применение одновременно и к строкам, и к столбцам ( шахматное разбиение ) области расчетов.

Рассмотренная схема чередования строк не требует, по сравнению с методом Якоби, какой-либо дополнительной памяти и обеспечивает однозначность решения при многократных запусках программы. Но следует заметить, что оба рассмотренных в данном пункте подхода могут получать результаты, которые не совпадут с решением задачи Дирихле, найденным при помощи последовательного алгоритма. Кроме того, эти вычислительные схемы имеют меньшую область и худшую скорость сходимости, чем исходный вариант метода Гаусса – Зейделя.