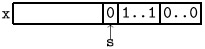
Порождение комбинаторных объектов
2.3. Подмножества
2.3.1.
Для заданных n и k (  ) перечислить
все k -элементные подмножества множества {1..n} }.
) перечислить
все k -элементные подмножества множества {1..n} }.
Решение. Будем представлять каждое подмножество
последовательностью x[1]..x[n] нулей и единиц
длины n, в которой ровно k единиц. (Другой способ
представления разберем позже.) Такие последовательности
упорядочим лексикографически (см. выше). Очевидный способ
решения задачи - перебирать все последовательности как
раньше, а затем отбирать среди них те, у которых k единиц - мы отбросим, считая его неэкономичным (число
последовательностей с k единицами может быть много
меньше числа всех последовательностей). Будем искать такой
алгоритм, чтобы получение очередной последовательности
требовало не более {C  n} действий.
n} действий.
В каком случае s -ый член последовательности можно увеличить, не меняя предыдущие? Если x[s] меняется с 0 на 1, то для сохранения общего числа единиц нужно справа от х[s] заменить 1 на 0. Для этого надо, чтобы справа от x[s] единицы были. Если мы хотим перейти к непосредственно} следующему, то x[s] должен быть первым справа} нулем, за которым стоят единицы. Легко видеть, что х[s+1]=1 (иначе х[s] не первый). Таким образом надо искать наибольшее s, для которого х[s]=0, x[s+1]=1:
За х[s+1] могут идти еще несколько единиц, а после них несколько нулей. Заменив х[s] на 1, надо выбрать идущие за ним члены так, чтобы последовательность была бы минимальна с точки зрения нашего порядка, т.е. чтобы сначала шли нули, а потом единицы. Вот что получается:

![\begin{quote}
алгоритм перехода к следующей за {х[1]..x[n]}
последовательности (предполагаем, что она есть):
\end{quote}](/sites/default/files/tex_cache/ae78f12d7d9966c9923ca891c5728658.png)
s := n - 1;
while not ((x[s]=0) and (x[s+1]=1)) do begin
| s := s - 1;
end;
{s - член, подлежащий изменению с 0 на 1}
num:=0;
for k := s to n do begin
| num := num + x[k];
end;
{num - число единиц на участке x[s]...x[n], число нулей
равно (длина - число единиц), т.е. (n-s+1) - num}
x[s]:=1;
for k := s+1 to n-num+1 do begin
| x[k] := 0;
end;
{осталось поместить num-1 единиц в конце}
for k := n-num+2 to n do begin
| x[k]:=1;
end;Другой способ представления подмножеств - это перечисление их элементов. Чтобы каждое подмножество имело ровно одно представление, договоримся перечислять элементы в возрастающем порядке. Приходим к такой задаче.
2.3.2. Перечислить все возрастающие последовательности длины k из чисел 1..n в лексикографическом порядке. (Пример: при n=5, k=2 получаем: 12 13 14 15 23 24 25 34 35 45.)
Решение. Минимальной будет последовательность 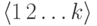 ; максимальной -
; максимальной - 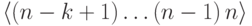 . В каком
случае s -ый член последовательности можно
увеличить? Ответ: если он меньше n-k+s. После
увеличения s -го элемента все следующие должны
возрастать с шагом 1. Получаем такой алгоритм перехода
к следующему:
. В каком
случае s -ый член последовательности можно
увеличить? Ответ: если он меньше n-k+s. После
увеличения s -го элемента все следующие должны
возрастать с шагом 1. Получаем такой алгоритм перехода
к следующему:
s:=n;
while not (x[s] < n-k+s) do begin
| s:=s-1;
end;
{s - номер элемента, подлежащего увеличению};
x[s] := x[s]+1;
for i := s+1 to n do begin
| x[i] := x[i-1]+1;
end;2.3.3.
Пусть мы решили представлять k -элементные
подмножества множества {1..n} убывающими
последовательностями длины k, упорядоченными
по-прежнему лексикографически. (Пример: 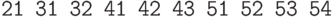 .) Как выглядит тогда алгоритм
перехода к следующей?
.) Как выглядит тогда алгоритм
перехода к следующей?
Ответ. Ищем наибольшее s, для которого х[s+1]+1 < x[s]. (Если такого s нет, полагаем s=0.) Увеличив x[s+1] на 1, кладем остальные минимально возможными ( x[t]=k+1-t для t>s ).
2.3.4. Решить две предыдущие задачи, заменив лексикографический порядок на обратный (раньше идут те, которые больше в лексикографическом порядке).
2.3.5.
Перечислить все вложения (функции, переводящие разные
элементы в разные) множества \{1..k} в {1..n} }
(предполагается, что  ). Порождение
очередного элемента должно требовать не более
). Порождение
очередного элемента должно требовать не более  действий.
действий.
Указание. Эта задача может быть сведена к перечислению подмножеств и перестановок элементов каждого подмножества.
2.4. Разбиения
2.4.1. Перечислить все разбиения целого положительного числа n на целые положительные слагаемые (разбиения, отличающиеся лишь порядком слагаемых, считаются за одно). (Пример: n=4, разбиения 1+1+1+1, 2+1+1, 2+2, 3+1, 4.)
Решение. Договоримся, что (1) в разбиениях слагаемые идут в невозрастающем порядке, (2) сами разбиения мы перечисляем в лексикографическом порядке. Разбиение храним в начале массива x[1]..x[n], при этом количество входящих в него чисел обозначим k. В начале x[1]=...=x[n]=1, k=n, в конце x[1]=n, k=1.
В каком случае x[s] можно увеличить, не меняя предыдущих? Во-первых, должно быть x[s-1]>x[s] или s=1. Во-вторых, s должно быть не последним элементом (увеличение s надо компенсировать уменьшением следующих). Увеличив s, все следующие элементы надо взять минимально возможными.
s := k - 1;
while not ((s=1) or (x[s-1] > x[s])) do begin
| s := s-1;
end;
{s - подлежащее увеличению слагаемое}
x [s] := x[s] + 1;
sum := 0;
for i := s+1 to k do begin
| sum := sum + x[i];
end;
{sum - сумма членов, стоявших после x[s]}
for i := 1 to sum-1 do begin
| x [s+i] := 1;
end;
k := s+sum-1;2.4.2.
Представляя по-прежнему разбиения как невозрастающие
последовательности, перечислить их в порядке, обратном
лексикографическому (для n=4, например, должно быть 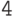 ,
, 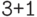 ,
,  ,
, 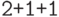 ,
,  ).
).
Указание. Уменьшать можно первый справа член, не равный 1 ; найдя его, уменьшим на 1, а следующие возьмем максимально возможными (равными ему, пока хватает суммы, а последний - сколько останется).
2.4.3.
Представляя разбиения как неубывающие последовательности,
перечислить их в лексикографическом порядке. Пример для 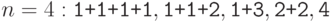 .
.
Указание. Последний член увеличить нельзя, а предпоследний - можно; если после увеличения на 1 предпоследнего члена за счет последнего нарушится возрастание, то из двух членов надо сделать один, если нет, то последний член надо разбить на слагаемые, равные предыдущему, и остаток, не меньший его.
2.4.4.
Представляя разбиения как неубывающие последовательности,
перечислить их в порядке, обратном лексикографическому.
Пример для 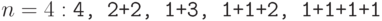 .
.
Указание.
Чтобы элемент x[s] можно было уменьшить, необходимо,
чтобы s=1 или x[s-1] < x[s]. Если x[s] не
последний, то этого и достаточно. Если он последний, то
нужно, чтобы ![\hbox{\texttt{x[s-1]}}\le\lfloor\hbox{\texttt{x[s]/2}}\rfloor](/sites/default/files/tex_cache/811537699e202bff38fb6d57c2b6f1fb.png) или s=1. (Здесь
или s=1. (Здесь  обозначает целую
часть
обозначает целую
часть  .)
.)