Лекция 4: Параллельные и сетевые технологии решения задач линейного программирования
Параллельный аналог "симплекс-метода"
Пример
Рассмотрим задачу линейного программирования
Z = 26x + 20y + 21z -> max (4.6)
при ограничениях
q1 = 2x + 7y - 76z + 222 >= 0
q2 = - 8x +9y - 8z + 64 >= 0
q3 = - 8x + 13y -24z + 96 >= 0 (4.7)
q4 = - x - 6y - z + 70 >= 0
q5 = - 2x - 7y - 2z + 90 >= 0
q6 = 33x + 3y +22z - 165 >= 0
и при условии x>= 0, y >= 0, z >= 0.
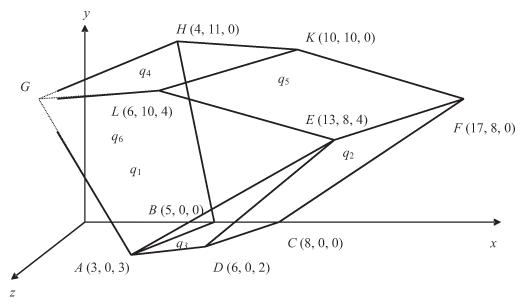
Ограничения и условия образуют многогранник R(ABCDEFGHKL) допустимых решений, представленный на рис. 4.4.
Формально мы не знаем R, и множество граней — действительных и возможных — этого многогранника представлено системой уравнений:
q1 = 2x + 7y - 76z + 222 = 0
q2 = - 8x +9y - 8z + 64 = 0
q3 = - 8x + 13y -24z + 96 = 0
q4 = - x - 6y - z + 70 = 0
q5 = - 2x - 7y - 2z + 90 = 0 (4.8)
q6 = 33x + 3y +22z - 165 = 0
q7 = x = 0
q8 = y = 0
q9 = z = 0
В результате решения первой же подсистемы трех уравнений (n = 3) системы (4.8) получаем координаты вершины E многогранника R
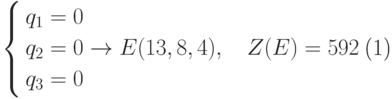 |
( 4.9) |
Постараемся "сместиться" в ту вершину, смежную вершине E, т.е. соединенную с ней ребром (в одну из вершин A, D, L, F ), в которой целевая функция Z имеет максимальное значение, превышающее Z(E).
Ребра, исходящие из вершины, определяются подсистемами n-1 плоскостей, пересекающихся в этой вершине, т.е. образующими ее.
В данном случае подсистема 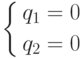 . определяет несуществующее ребро. Пока мы знаем
это только по рисунку. Подсистема
. определяет несуществующее ребро. Пока мы знаем
это только по рисунку. Подсистема
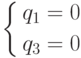
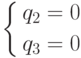
Значит, q1, q2, q3 — это лишь наше начальное представление о множестве плоскостей — граней, пересекающихся в вершине E. Нам необходимо развить это представление до полного.
Тогда выясним все множество граней, образующих вершину E,
подстановкой ее координат во все другие уравнения (9.8) и испытанием на
получение тождества. Находим 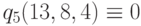 . Добавляем q5 в (4.9),
полагаем полностью известным число p = 4 ребер, образующих вершину E. Т.е. вместо (4.9) получаем
. Добавляем q5 в (4.9),
полагаем полностью известным число p = 4 ребер, образующих вершину E. Т.е. вместо (4.9) получаем
 |
( 4.10) |
Первая такая система имеет вид
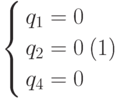 |
( 4.11) |
Можно показать, что в выпуклом многограннике несуществующее ребро не вызовет появления "ложной" вершины, и достаточно проверить (4.7).
Системы
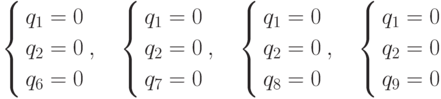
Следующая испытываемая система линейных уравнений на основе двух уравнений из (4.10) и не входящих в (4.10) уравнений из (4.8), имеет вид
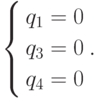
Следующая испытываемая система имеет вид
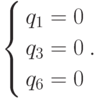
Т.к. мы нашли вершину на "другом конце" ребра, анализ данного ребра прекращаем.
Следующее исследуемое ребро, исходящее из вершины E, определяется подсистемой

Первая же система 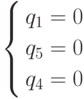 . определяет вершину L (6, 10, 4).
Однако Z(L) =
440 < 592.
. определяет вершину L (6, 10, 4).
Однако Z(L) =
440 < 592.
Следующее возможное ребро, исходящее из вершины E, определяется комбинацией