Лекция 4: Параллельные и сетевые технологии решения задач линейного программирования
Общий алгоритм
-
Формируем систему m + n уравнений
действительных и возможных границ многогранника R допустимых решений. Эта система уравнений отображает m заданных ограничений и n условий неотрицательности решения.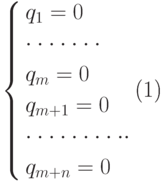
( 4.13) -
Решая совместно подмножество n уравнений этой системы, находим одну из вершин X0 многогранника R. Находим значение z0 целевой функции в точке X0.
-
Дополним систему n уравнений, первоначально породившую вершину X0, теми уравнениями, которым X0 также удовлетворяет. Получим систему p >= n уравнений, порождающих вершину X0.

( 4.14) Примечание 1. Теперь наша задача — переместиться вдоль одного из ребер, исходящих из вершины X0, в смежную вершину X1, такую, что Z(X1) > Z(X0). При этом, желая ускорить процесс (хотя выбор стратегии нуждается в обосновании), будем среди всех смежных вершин искать ту вершину X1, в которой достигается максимальное увеличение значения целевой функции. Каждое ребро описывается системой n - 1 уравнений из состава p уравнений, породивших испытываемую вершину X0. Введем переменную p, первоначально приняв p = n
-
Выбирая из (4.14) по n - 1 уравнений, будем получать систему, которая определяет некоторое ребро, исходящее из X0. Всего таких подсистем может быть Cpn - 1.
-
Последовательно испытываем данное ребро на его пересечение с теми из m гранями из (4.13), которые не вошли в состав (4.14). Т.е. дополняем нашу систему n - 1 уравнений очередной испытываемой гранью. Получаем систему n уравнений и решаем ее. Возможны следующие варианты.
-
Система не имеет решения, имеет не единственное решение или решение содержит отрицательные компоненты. Переходим к испытанию следующей грани.
-
Система имеет неотрицательное решение, но это решение не удовлетворяет всем m ограничениям задачи, т.е. находится вне R. Переходим к испытанию следующей грани.
-
Система имеет неотрицательное решение
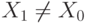 ,
удовлетворяющее всем m ограничениям задачи. Значит, найдена
смежная
вершина. Если Z(X1) < Z(X0), переходим к испытанию
следующего ребра
— к выполнению шага 6. Если Z(X1) = Z(X0), запоминаем вершину X1.
Это для случая, если в результате проводимых испытаний оказалось, что
точка X0 — решение задачи. Тогда необходимо знать все
вершины,
образующие решение, чтобы построить общее параметрическое выражение.
Переходим к испытанию следующего ребра. Если Z(X1) > Z(X0),
запоминаем точку X1 в данном качестве и переходим к испытанию
следующего ребра.
,
удовлетворяющее всем m ограничениям задачи. Значит, найдена
смежная
вершина. Если Z(X1) < Z(X0), переходим к испытанию
следующего ребра
— к выполнению шага 6. Если Z(X1) = Z(X0), запоминаем вершину X1.
Это для случая, если в результате проводимых испытаний оказалось, что
точка X0 — решение задачи. Тогда необходимо знать все
вершины,
образующие решение, чтобы построить общее параметрическое выражение.
Переходим к испытанию следующего ребра. Если Z(X1) > Z(X0),
запоминаем точку X1 в данном качестве и переходим к испытанию
следующего ребра.
Примечание 2. Возможна стратегия, при которой смещение производится в первую же найденную вершину с превышающим значением целевой функции. Есть вариант, что это — более правильная стратегия, т.к. значительное увеличение значения целевой функции на данном шаге может привести в дальнейшем к увеличению числа шагов: мы ничего не знаем о особенностях многогранника решений. Мы же здесь рассматриваем стратегию, при которой отыскивается смежная вершина с максимальным превышением целевой функции.
-
-
Перебрав все грани для одной подсистемы n - 1 линейных уравнений (для одного ребра), формируем другую подсистему таких уравнений на основе (4.14). Анализируем ее совместно со всеми m + n - p уравнениями из (4.13).
-
Таким образом, исследовав все ребра, исходящие из X0, мы можем найти ту смежную вершину X1, где целевая функция максимально превышает ее значение в исходной вершине. Перемещаемся в эту вершину, полагая X0 = X1. Система (4.14) теперь — та система n уравнений, решение которой породило X1. Дополняем ее уравнениями других граней, проходящих через X1. Получаем p >= n. Начинаем весь процесс перемещения сначала. Однако первое ребро, определяемое первыми n - 1 уравнениями (4.14), это ребро, которое ведет в вершину, из которой мы вышли. Т.е. первую комбинацию n - 1 граней следует пропустить.
-
Если не удается найти вершину, в которой значение целевой функции превышает ранее найденное, то мы нашли решение. Одновременно мы нашли и сохранили те смежные (проанализированной вершине!) вершины, в которых значения целевой функции равны. Однако мы могли найти не все вершины, обладающие одним, максимальным, значением Z. Ведь мы двигались только по ребрам, исходящим из предыдущей анализируемой вершины. "Напротив" этой вершины могут быть другие вершины с тем же значением целевой функции, и в эти вершины не ведут ребра из данной. Однако на основе свойств выпуклого многогранника можно заключить, что отношение взаимной смежности связывает все вершины, образующие решение задачи ЛП. Т.е. вершины-решения, не смежные друг другу, являются смежными другим вершинам-решениям. Существует путь вдоль ребер, связывающий вершины-решения. Тогда можно построить алгоритм выявления всех вершин R — решений задачи ЛП.
-
Пусть найденные уже вершины-решения образуют множество A. Дополним его последней найденной вершиной. Выбираем первую из ранее запомнившихся вершин из A с равным, максимальным, значением целевой функции и делаем ее опорной, X0.
-
Выполняем шаги 4-8 для поиска вершины многогранника R с более высоким значением Z, чем значение Z(X0). Конечно, мы такой вершины найти не можем. Но мы можем найти новую вершину X, не входящую в множество A, такую, что Z(X) = Z(X0). Включаем вершину X в A, полагаем X0 := X. Продолжаем выполнение данного пункта до тех пор, пока множество A не перестанет пополняться новыми вершинами. Производим параметрическую запись (4.4) общего решения задачи.
-
Сложность алгоритма
Если считать, что чаще всего из одной вершины исходят n граней, то число решаемых систем n линейных уравнений при поиске смежных вершин определяется как
r = n x (m + n - n) = n x m.
Число вершин k, по которым производится перемещение в поисках
решения, предсказать трудно. Однако очевидно, что k << Cnm +
n, т.к.
лишь локально затрагивается некоторый "бок" многогранника R.
Считая, как и раньше,  , можно оценить сложность решения
данным методом, как O(kn5). Эта сложность является
полиномиальной.
, можно оценить сложность решения
данным методом, как O(kn5). Эта сложность является
полиномиальной.
План параллельных вычислений
Воспользуемся в основном той же схемой вычислений, что и в разделе 4.1.
Пусть все процессоры ВС или используемые станции локальной сети обладают своим номером и знают количество используемых средств. Как показывалось ранее, они все начинают решать "свои" системы линейных уравнений. Здесь уже можно применить различные стратегии. Одна из них: пусть хотя бы один процессор нашел вершину многогранника R. Ее можно взять за вершину X0.
Другая стратегия заключается в том, чтобы дать возможность всем участвующим процессорам найти по одной вершине R. Вершину с максимальным значением целевой функции Z можно взять за X0.
Выбрав вершину X0, все процессоры начинают решать "свои" варианты систем линейных уравнений в поисках смежных вершин с превышающим значением целевой функции. Согласовав действия при нахождении вершины X1 и приняв X0 := X1, они продолжают процесс движения по ребрам R.
