Лекция 4: Параллельные и сетевые технологии решения задач линейного программирования

Очередная решаемая система уравнений

имеет не отрицательное решение (13,625, 8,7, 4,175). Проверяем выполнение ограничений (9.7), не представленных в решенной системе. Находим, что q₁(13,625, 8,7, 4,195) < 0. Этой проверки достаточно для вывода о том, что найденная точка не является вершиной многогранника R.

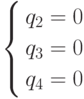
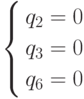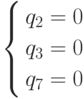Системы . и . имеют решение в отрицательной области.

Система . определяет вершину D (6, 0, 2), для которой Z(D) = 198 < 592.

Следующее возможное ребро по (4.10) определяется парой граней

Решаем совместно с остальными гранями, не входящими в (10): q₄ = 0, q₆ = 0, q₇ = 0, q₈ = 0, q₉ = 0.

Система

не имеет решения, ранг матрицы системы не равен рангу расширенной матрицы.

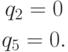
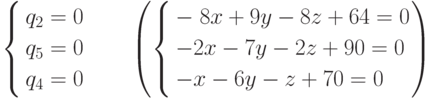
Система 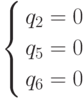. имеет отрицательное решение.

Система 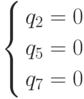. имеет неотрицательное решение, при котором q₁ < 0. Найденная точка не является вершиной R.

Система 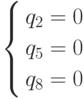. не имеет решения.

Система

имеет неотрицательное решение — точку F (17, 8, 0), удовлетворяющую всем ограничениям: q₁(17, 8, 0) > 0, q₃ (17, 8, 0) > 0, q₄(17, 8, 0) > 0, q₆(17, 8, 0) > 0. Точка F — вершина многогранника R. Z(F) = 602 > 592.

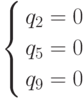
Таким образом, мы нашли вершину F, смежную вершине E, с превышающим значением целевой функции. Однако поиск всех вершин на основе (4.10), смежных вершин E, следует продолжить. Ведь формально возможна и другая вершина, с еще большим значением целевой функции.

Перебор продолжаем на основе ребра

хотя мы видим по рисунку, что такого ребра нет.

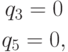
Ищем точки пересечения этого ребра со всеми гранями R, не вошедшими в (4.10).

Система уравнений 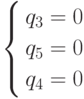. имеет решение (0,875, 10, 9,125).

При проверке выполнения первого же ограничения оказывается, что q₁(0,875, 10, 9,125) < 0. Найденная точка действительно не является вершиной R.

Система 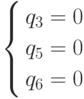. имеет отрицательное решение.

Система 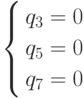. имеет решение (0, 10,144, 9,5), не удовлетворяющее первому же ограничению.

Система 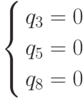. имеет отрицательное решение.

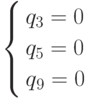Система . имеет не отрицательное решение (22,96, 6,44, 0), не удовлетворяющее ограничениям.

Таким образом, анализ всех возможных вершин, смежных вершине E, закончен. Мы нашли единственную вершину F(17, 8, 0), где значение целевой функции Z(17, 8, 0) = 602 превышает ее значение в точке E. Система уравнений, определившая эту вершину, имеет вид

Если бы мы нашли несколько вершин с одинаковым значением целевой функции, то были бы возможны различные стратегии дальнейших действий. Мы здесь рассматриваем случай, когда для дальнейшего поиска фиксируется одна из таких вершин. Других граней, которым принадлежит точка F, нет. Смещаемся в эту вершину, полагаем p = 3.

Начинаем весь процесс поиска смежной вершины с максимальным (среди смежных вершин) значением целевой функции Z, обязательно превышающим значение Z(F).

Первое возможное ребро, исходящее из F, определяется уравнениями

Однако эта комбинация возвращает нас в ту вершину, которую мы уже исследовали. Поэтому сразу же переходим к следующему возможному ребру решая его совместно с гранями q₁, q₃, q₄, q₆, q₇, q₈.

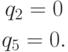
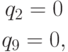
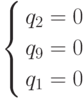
Система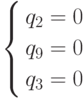

решалась ранее. Ее решение неположительно. (Если мы переупорядочим уравнения системы по индексам, то получим индексный код, по которому будем входить в таблицу с информацией о решенной ранее системе. Так мы реализуем самообучение в процессе решения.)

Система . решалась ранее. Ее решение также содержит отрицательный компонент.

Система

решается впервые. Ее не отрицательное решение не удовлетворяет всем ограничениям, q₃(17,8, 8,7, 0) < 0.

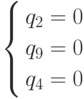
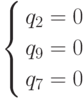Системы . и . имеют решения, содержащие отрицательные компоненты.

Система . определяет вершину C, Z(8, 0, 0) = 208 < 602.

Следующее исследуемое ребро определяется системой уравнений

Система 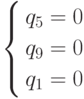. исследовалась раньше. Она не имеет решения.

Система 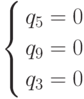. решалась ранее. Она определяет точку, не являющуюся вершиной R.

Система 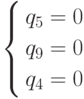. решается впервые. Она определяет точку K. Однако Z(10, 10, 0) = 460 < 602.

Таким образом, нам не удалось сместиться из вершины F в вершину с большим значением Z. Значит, найденная точка F определяет решение задачи ЛП.