m-сводимость и свойства перечислимых множеств
Перечислимые множества, дополнения которых продуктивны, называются креативными (creative; иногда это слово переводят как " творческие "). Название объясняется так: это множество (точнее, его дополнение) более изобретательно, чем любой алгоритмический процесс: если кто-то предлагает способ порождать некоторые элементы из дополнения, то в ответ можно указать элемент дополнения, который нельзя получить таким способом.
Как мы видим, творческие множества, перечислимые множества с эффективно неперечислимым дополнением и m -полные множества один и тот же класс, и любые два множества из этого класса в некотором смысле изоморфны (отличаются лишь вычислимой перестановкой).
Если множество продуктивно, то можно порождать его элементы следующим
индуктивным процессом. На первом шаге имеется пустое множество.
Применив к нему продуктивную функцию (е функцию,
существующую по определению продуктивного множества), мы получим
некоторый элемент. Он образует одноэлементное подмножество.
Применив к этому подмножеству продуктивную функцию, получим
другой элемент. К полученному двухэлементному подмножеству можно
снова применить продуктивную функцию и так далее. Получится
бесконечная вычислимая последовательность элементов
продуктивного множества. (Это мы уже делали, когда доказывали,
что эффективно неперечислимое множество содержит бесконечное
перечислимое
подмножество.) Но этот индуктивный процесс можно "
трансфинитно " продолжить, по крайней мере еще немного: имея
перечислимое подмножество нашего продуктивного множества
(множество членов последовательности), можно найти еще один
элемент продуктивного множества (так сказать, элемент
номер  ). Добавим его к последовательности, снова применим
продуктивную функцию, получится
). Добавим его к последовательности, снова применим
продуктивную функцию, получится 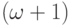 -ый элемент и так
далее, затем получится новая последовательность,
-ый элемент и так
далее, затем получится новая последовательность, 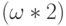 -й
элемент,
-й
элемент, 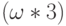 -й,...,
-й,..., 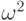 -й
элемент и т.д.
-й
элемент и т.д.
Но, конечно, получить таким образом алгоритм, перечисляющий продуктивное (и потому неперечислимое) множество, не удастся.
50. Не используя теорему о неподвижной точке (и теорему 42), покажите, что для всякого продуктивного множества A существует всюду определенная вычислимая функция f, для которой  влечет
влечет  . (Указание: чередуйте Wn с пустым множеством, как это делается
при доказательстве леммы к теореме 41.)
. (Указание: чередуйте Wn с пустым множеством, как это делается
при доказательстве леммы к теореме 41.)
Пары неотделимых множеств
В этом разделе мы сформулируем некоторые результаты, касающиеся пар непересекающихся перечислимых множеств. Эти результаты параллельны только что доказанным нами теоремам о m -полноте, продуктивности, эффективной неперечислимости и об изоморфизме m -полных множеств.
Пусть A и B два непересекающихся множества
(натуральных
чисел). Напомним, что они называются неотделимыми, если не
существует разрешимого множества, содержащего одно из них и не
пересекающегося с другим.
Это определение можно переформулировать так: если Wx и Wy два непересекающихся перечислимых множества,
содержащие A и B соответственно, то объединение  содержит не все натуральные числа. (Нам будет удобно
обозначать перечислимые множества через Wx и Wy,
считая,
что W главное универсальное множество.)
содержит не все натуральные числа. (Нам будет удобно
обозначать перечислимые множества через Wx и Wy,
считая,
что W главное универсальное множество.)
Теперь ясно, как можно сформулировать эффективный вариант этого
определения. Будем говорить, что непересекающиеся множества A
и B эффективно неотделимы, если существует вычислимая функция h с таким свойством: если  ,
, 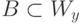 и
и  , то h(x,y) определено и
, то h(x,y) определено и 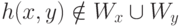 .
.
Определение неотделимости можно сформулировать чуть-чуть
иначе: не существует вычислимой функции 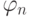 , которая была бы всюду определенной,
во всех точках множества A равнялась бы
нулю, а во всех точках множества B единице. (Будем считать,
что
, которая была бы всюду определенной,
во всех точках множества A равнялась бы
нулю, а во всех точках множества B единице. (Будем считать,
что  главная универсальная функция.) Соответственно
изменится и эффективный вариант: множества A и B сильно эффективно неотделимы, если существует всюду
определенная вычислимая
функция h, которая по любому n указывает
точку h(n), в которой функция
главная универсальная функция.) Соответственно
изменится и эффективный вариант: множества A и B сильно эффективно неотделимы, если существует всюду
определенная вычислимая
функция h, которая по любому n указывает
точку h(n), в которой функция 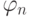 "
ошибается ".
Ошибка возможна трех видов: либо
"
ошибается ".
Ошибка возможна трех видов: либо 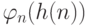 не
определено, либо
не
определено, либо 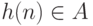 , но
, но 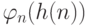 не
равно
нулю, либо
не
равно
нулю, либо  , но
, но 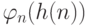 не равно
единице.
не равно
единице.
51. Покажите, что из сильной эффективной неотделимости вытекает эффективная неотделимость (что оправдывает используемую нами терминологию).
Обратное утверждение также верно, но доказывается несколько сложнее, и мы к нему еще вернемся.
Существуют ли сильно эффективно неотделимые перечислимые множества?
Легко понять, что стандартная диагональная конструкция дает пару
таких множеств, а именно множества 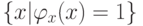 и
и 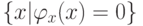 , для которых в качестве
функции h
можно взять тождественную функцию.
, для которых в качестве
функции h
можно взять тождественную функцию.
52. Проверьте это.
Продолжая нашу аналогию (между множествами и парами),
определим понятие m -сводимости для пар.
Здесь тоже будет два варианта.
Пусть 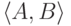 и
и 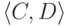 две
пары
непересекающихся перечислимых множеств ( A не пересекается
с B, а C с D ). Будем говорить, что
вычислимая всюду определенная функция f m -сводит
две
пары
непересекающихся перечислимых множеств ( A не пересекается
с B, а C с D ). Будем говорить, что
вычислимая всюду определенная функция f m -сводит 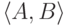 к
к 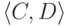 , если
, если 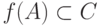 и
и 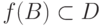 .
.
53. (а) Покажите, что если f сводит 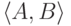 к
к 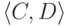 и C отделимо от D разрешимым
множеством, то
и A отделимо от B разрешимым множеством. (б) Покажите, что если f сводит
и C отделимо от D разрешимым
множеством, то
и A отделимо от B разрешимым множеством. (б) Покажите, что если f сводит 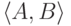 к
к 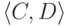 и пара
и пара 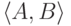 эффективно неотделима,
то и пара
эффективно неотделима,
то и пара 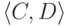 эффективно неотделима. (в) Покажите, что если f сводит
эффективно неотделима. (в) Покажите, что если f сводит 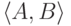 к
к 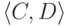 и пара
и пара 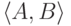 сильно эффективно
неотделима, то и пара
сильно эффективно
неотделима, то и пара 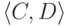 сильно эффективно
неотделима.
сильно эффективно
неотделима.
Определение сводимости можно усилить, потребовав дополнительно,
чтобы при 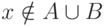 выполнялось
выполнялось 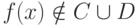 (другими словами, f должна
сводить A к C и
одновременно B к D ). В этом случае мы будем
говорить, что f сильно сводит пару
(другими словами, f должна
сводить A к C и
одновременно B к D ). В этом случае мы будем
говорить, что f сильно сводит пару 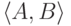 к
паре
к
паре 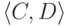 .
.
Теперь мы можем определить m -полноту и сильную m -полноту для пары непересекающихся перечислимых множеств, требуя m -сводимости (соответственно сильной m -сводимости) любой такой пары к данной.
54.
Покажите, что если пара является сильно эффективно неотделимой,
то она является сильно m -полной. (Указание. Пусть
пара 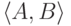 сильно эффективно неотделима,
а
сильно эффективно неотделима,
а 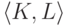 любая пара непересекающихся
перечислимых множеств. По любому натуральному числу x можно
построить вычислимую функцию
любая пара непересекающихся
перечислимых множеств. По любому натуральному числу x можно
построить вычислимую функцию 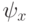 с таким свойством: если
с таким свойством: если 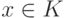 , то
, то 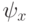 всюду определена и отличается
от единицы
лишь в конечном числе точек, причем все эти точки принадлежат A ;
если
всюду определена и отличается
от единицы
лишь в конечном числе точек, причем все эти точки принадлежат A ;
если 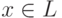 , то
, то 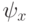 всюду определена и отличается от нуля лишь в
конечном числе точек, причем все эти точки принадлежат B ;
если
всюду определена и отличается от нуля лишь в
конечном числе точек, причем все эти точки принадлежат B ;
если 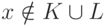 , то
, то 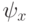 равна нулю на A и единице на B.
Чтобы построить
такую функцию, перечисляем K и L ; пока x не обнаружилось
в одном из этих множеств, добавляем в график
равна нулю на A и единице на B.
Чтобы построить
такую функцию, перечисляем K и L ; пока x не обнаружилось
в одном из этих множеств, добавляем в график 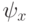 пары
вида
пары
вида  и
и 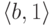 ;
когда x
обнаруживается, перестраиваемся. Далее остается воспользоваться
свойствами главной нумерации
;
когда x
обнаруживается, перестраиваемся. Далее остается воспользоваться
свойствами главной нумерации  и сильной эффективной
неотделимостью A и B.)
и сильной эффективной
неотделимостью A и B.)
55. Покажите, что всякая m -полная пара является сильно эффективно неотделимой. (Указание: сильно эффективно неотделимая пара существует и к ней сводится.)
Из сформулированных в качестве задач утверждений вытекает, что свойства m -полноты, сильной m -полноты и сильной эффективной неотделимости пар непересекающихся множеств эквивалентны. Можно доказать, что и кажущееся более слабым свойство эффективной неотделимости эквивалентно им. Рассуждение при этом аналогично доказательству теоремы 42 о том, что всякое креативное множество является m -полным. Заметим, что разница между эффективной неотделимостью и сильной эффективной неотделимостью примерно такая же, как между продуктивностью и эффективной неперечислимостью.
56. Пусть 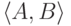 эффективно неотделимая пара непересекающихся перечислимых множеств. Покажите, что она является сильно m -полной. (Указание. Пусть K и L произвольные непересекающиеся перечислимые множества. Пусть h функция из определения эффективной неотделимости (множеств A и B ). С помощью теоремы о неподвижной точке постройте всюду определенные вычислимые функции x(n) и y(n) с такими свойствами: (1) если
эффективно неотделимая пара непересекающихся перечислимых множеств. Покажите, что она является сильно m -полной. (Указание. Пусть K и L произвольные непересекающиеся перечислимые множества. Пусть h функция из определения эффективной неотделимости (множеств A и B ). С помощью теоремы о неподвижной точке постройте всюду определенные вычислимые функции x(n) и y(n) с такими свойствами: (1) если 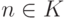 , то Wx(n)=A,
, то Wx(n)=A, 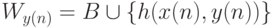 ; (2) если
; (2) если 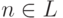 , то
, то 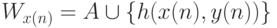 , Wy(n)=B ; (3) если
, Wy(n)=B ; (3) если 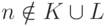 , то Wx(n)=A, Wy(n)=B. Выведите отсюда, что при
, то Wx(n)=A, Wy(n)=B. Выведите отсюда, что при 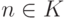 значение h(x(n),y(n)) определено и принадлежит A, при
значение h(x(n),y(n)) определено и принадлежит A, при 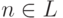 значение h(x(n),y(n)) определено и принадлежит B, а при
значение h(x(n),y(n)) определено и принадлежит B, а при 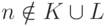 значение h(x(n),y(n)) определено и лежит вне
значение h(x(n),y(n)) определено и лежит вне  .)
.)
Итак, все четыре сформулированных свойства эквивалентны. Продолжая нашу аналогию, можно доказать изоморфность любых двух пар эффективно неотделимых множеств, для чего предварительно научиться получать сколь угодно много чисел, " эквивалентных " данному с точки зрения пары эффективно неотделимых множеств.
Более точно, пусть имеются непересекающиеся множества A и B. Назовем два числа 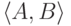 -эквивалентными в любом из следующих трех случаев: оба они принадлежат A, оба они принадлежат B или оба они не принадлежат
-эквивалентными в любом из следующих трех случаев: оба они принадлежат A, оба они принадлежат B или оба они не принадлежат  . (Таким образом, есть три класса эквивалентности множество A, множество B и остаток.)
. (Таким образом, есть три класса эквивалентности множество A, множество B и остаток.)
57. Пусть 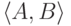 сильно m -полная пара непересекающихся перечислимых множеств. Покажите, что по любому числу k можно алгоритмически получать сколь угодно много различных чисел, которые будут
сильно m -полная пара непересекающихся перечислимых множеств. Покажите, что по любому числу k можно алгоритмически получать сколь угодно много различных чисел, которые будут 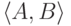 -эквивалентны k. (Указание: действуйте по аналогии с доказательствами теоремы 22 и леммы к теореме 41.)
-эквивалентны k. (Указание: действуйте по аналогии с доказательствами теоремы 22 и леммы к теореме 41.)
58. Пусть  и
и 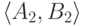 две сильно m -полные пары непересекающихся перечислимых множеств. Тогда они вычислимо изоморфны в следующем смысле: существует вычислимая перестановка (биекция) i : N -> N, при которой i(A1)=A2 и i(B1)=B2. (Указание: действуйте по аналогии с доказательствами теорем 23 и 41.)
две сильно m -полные пары непересекающихся перечислимых множеств. Тогда они вычислимо изоморфны в следующем смысле: существует вычислимая перестановка (биекция) i : N -> N, при которой i(A1)=A2 и i(B1)=B2. (Указание: действуйте по аналогии с доказательствами теорем 23 и 41.)
