Арифметическая иерархия
Классы Sigma _n и Pi _n
Мы уже говорили, что перечислимые множества можно эквивалентно определить как проекции разрешимых множеств:
множество 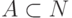 перечислимо тогда и только тогда, когда
существует разрешимое множество
перечислимо тогда и только тогда, когда
существует разрешимое множество  ,
проекцией которого оно
является. Если отождествлять множества со свойствами, то можно
сказать, что свойство A(x) натуральных чисел перечислимо тогда
и только тогда, когда его можно представить в виде
,
проекцией которого оно
является. Если отождествлять множества со свойствами, то можно
сказать, что свойство A(x) натуральных чисел перечислимо тогда
и только тогда, когда его можно представить в виде

где B(x,y) некоторое разрешимое свойство.
(В этом разделе мы предполагаем знакомство читателя с простейшими логическими обозначениями: квантор  читается как " существует x ", квантор
читается как " существует x ", квантор  читается как " для всех x ", знак
читается как " для всех x ", знак 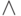 читается как " и" и называется конъюнкцией, знак
читается как " и" и называется конъюнкцией, знак 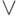 читается как " или" и называется дизъюнкцией, знак
читается как " или" и называется дизъюнкцией, знак 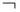 читается как " неверно, что" и называется отрицанием. Как и раньше, знак
читается как " неверно, что" и называется отрицанием. Как и раньше, знак  означает равносильность.)
означает равносильность.)
Возникает естественный вопрос: что можно сказать про другие наборы кванторов? Например, какие свойства представимы в виде

где C разрешимое свойство троек натуральных чисел? Легко
сообразить, что это по-прежнему перечислимые множества. В самом деле,
два подряд идущих квантора одного вида можно заменить одним,
использовав вычислимую нумерацию пар (которую мы обозначаем
квадратными скобками): свойство C', для которого ![C'(x,[y,z]) \Leftrightarrow C(x,y,z)](/sites/default/files/tex_cache/c15fb9aa0fe62c72da58f0229905c9c5.png) , также разрешимо, и
, также разрешимо, и  .
.
Другой вопрос: какие свойства представимы в виде

где B(x,y) некоторое разрешимое свойство? Ответ: те, отрицания которых перечислимы (как иногда говорят, коперечислимые ). В самом деле, переходя к отрицаниям, имеем

а разрешимые свойства остаются разрешимыми при переходе к отрицаниям.
Дадим общее определение. Свойство A принадлежит классу  , если его можно представить в виде
, если его можно представить в виде

(в правой части стоит n чередующихся кванторов) для некоторого разрешимого свойства B. Если в правой части поставить n чередующихся кванторов, начиная с квантора всеобщности 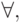 то получится определение класса
то получится определение класса  .
.
Отметим два свойства, которые мы по существу уже доказали:
Теорема 51. (а) Определение класса  [
[  ] не
изменится, если в
правой части разрешить большее число кванторов и требовать,
чтобы первый квантор был квантором существования [всеобщности] и
число групп одинаковых стоящих рядом
кванторов равнялось n. (б) Отрицания свойств из класса
] не
изменится, если в
правой части разрешить большее число кванторов и требовать,
чтобы первый квантор был квантором существования [всеобщности] и
число групп одинаковых стоящих рядом
кванторов равнялось n. (б) Отрицания свойств из класса  принадлежат
классу
принадлежат
классу  и наоборот.
и наоборот.
Для доказательства первого утверждения достаточно соединять рядом стоящие одинаковые кванторы с помощью нумерации пар. Для доказательства второго надо проносить отрицание внутрь (меняя тип квантора), пока оно не окажется у разрешимого свойства (где оно роли не играет).
Мы говорили о свойствах; на языке множеств можно сказать так:
множества класса  получаются из разрешимых с помощью
последовательности операций " проекция-дополнение-проекция-дополнение-...-проекция", в которой всего n операций
проекции. Каждая операция проекции уменьшает
размерность множества (число аргументов у свойства) на единицу,
так что начинать надо с разрешимых подмножеств Nn+1.
получаются из разрешимых с помощью
последовательности операций " проекция-дополнение-проекция-дополнение-...-проекция", в которой всего n операций
проекции. Каждая операция проекции уменьшает
размерность множества (число аргументов у свойства) на единицу,
так что начинать надо с разрешимых подмножеств Nn+1.
Теорема 52. Пересечение и объединение двух множеств из класса  принадлежит
принадлежит  . Пересечение и объединение двух
множеств из класса
. Пересечение и объединение двух
множеств из класса  принадлежит
принадлежит  .
.
Удобно выразить это утверждение на логическом языке, сказав, что
конъюнкция и дизъюнкция любых двух свойств из класса  лежат в том же классе (аналогично для
лежат в том же классе (аналогично для  ). На этом же языке удобно
провести и доказательство: если, скажем,
). На этом же языке удобно
провести и доказательство: если, скажем,
![A(x) \Leftrightarrow \exists\ y\ \forall\ z\ B(x,y,z),
\\
C(x) \Leftrightarrow \exists\ u \forall\ v\ D(x,u,v),
\\
то
\\
A(x) \wedge C(x) \Leftrightarrow \exists\ y \exists\ u \forall\ z \forall\ v\ [B(x,y,z) \wedge D(x,u,v)],](/sites/default/files/tex_cache/fa38807402be0b2f6939f3052b1b61a5.png)
записанное в квадратных скобках свойство разрешимо и остается
только соединить пары кванторов в один, как объяснялось выше.
Аналогично можно действовать для классов  и
и  при произвольном n.
при произвольном n.
Мы определяли классы  и
и  для множеств
натуральных чисел; аналогичным образом это можно сделать и для
множеств пар натуральных чисел, троек и вообще любых "
конструктивных объектов". Заметим, что
проекция множества пар, принадлежащего классу
для множеств
натуральных чисел; аналогичным образом это можно сделать и для
множеств пар натуральных чисел, троек и вообще любых "
конструктивных объектов". Заметим, что
проекция множества пар, принадлежащего классу  ,
также принадлежит
,
также принадлежит  (поскольку два квантора
существования в начале можно объединить в один).
(поскольку два квантора
существования в начале можно объединить в один).
Добавляя фиктивные кванторы, легко убедиться, что каждый из двух
классов  и
и  содержится в каждом из
классов
содержится в каждом из
классов  и
и  . Можно написать еще так:
. Можно написать еще так:

Теорема 53. Классы  и
и  " наследственны вниз" относительно m -сводимости:
если A <=m B и
" наследственны вниз" относительно m -сводимости:
если A <=m B и  [
[  ],
то и
],
то и  [
[  ].
].
В самом деле, пусть A сводится к B с помощью всюду
определенной вычислимой функции f, то есть 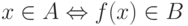 . Пусть B принадлежит,
например,
классу
. Пусть B принадлежит,
например,
классу 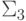 , то есть
, то есть

где R некоторое разрешимое свойство. Тогда

и осталось заметить, что R(f(x),y,z,u) (как свойство
четверки  ) разрешимо.
) разрешимо.
63. Докажите, что если множество A принадлежит классу  , то множество A x A также принадлежит этому классу.
, то множество A x A также принадлежит этому классу.
64. Докажите, что если множества A и B принадлежат классу  , то их разность A \ B принадлежит
классу
, то их разность A \ B принадлежит
классу  .
.
