Универсальные функции и неразрешимость
Универсальные функции
Сейчас мы построим пример перечислимого множества, не являющегося разрешимым. При этом будет использоваться так называемая универсальная функция.
Говорят, что функция U двух натуральных аргументов является универсальной для класса вычислимых функций одного аргумента, если для каждого n функция
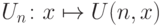
("сечение" функции U при фиксированном n ) является вычислимой и если все вычислимые функции (одного аргумента) встречаются среди Un. (Напомним, что ни функция U, ни вычислимые функции одного аргумента не обязаны быть всюду определенными.)
Аналогичное определение можно дать и для других классов функций (одного аргумента): например, функция U двух аргументов будет универсальной для класса всех всюду определенных вычислимых функций одного аргумента, если ее сечения Un являются всюду определенными вычислимыми функциями одного аргумента и исчерпывают все такие функции. Очевидно, универсальные функции существуют для любых счетных классов (и только для них).
Ключевую роль в этом разделе играет такой факт:
Теорема 6.Существует вычислимая функция двух аргументов, являющаяся универсальной функцией для класса вычислимых функций одного аргумента.
Запишем все программы, вычисляющие функции одного аргумента, в вычислимую последовательность p0, p1, ... (например, в порядке возрастания их длины). Положим U(i,x) равным результату работы i -ой программы на входе x. Тогда функция U и будет искомой вычислимой универсальной функцией. Сечение Ui будет вычислимой функцией, вычисляемой программой pi. Алгоритм, вычисляющий саму функцию U, есть по существу интерпретатор для используемого языка программирования (он применяет первый аргумент ко второму, если отождествить программу и ее номер).
15. Все сечения Un некоторой функции U двух аргументов вычислимы. Следует ли отсюда, что функция U вычислима?
16. Дайте (естественное) определение понятия вычислимой функции трех аргументов, универсальной для класса вычислимых функций двух аргументов, и докажите ее существование.
Для множеств используется аналогичная терминология: множество 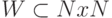 называют универсальны для некоторого класса множеств натуральных чисел, если все сечения
называют универсальны для некоторого класса множеств натуральных чисел, если все сечения
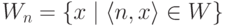
множества W принадлежат этому классу и других множеств в классе нет.
Теорема 7.Существует перечислимое множество пар натуральных чисел, универсальное для класса всех перечислимых множеств натуральных чисел.
Рассмотрим область определения универсальной функции U. Она будет универсальным перечислимым множеством, поскольку всякое перечислимое множество является областью определения некоторой вычислимой функции Un.
17. Как построить универсальное множество, исходя из того, что всякое перечислимое множество есть множество значений некоторой функции Un?
18. Существует ли разрешимое множество пар натуральных чисел, универсальное для класса всех разрешимых множеств натуральных чисел?
Диагональная конструкция
В предыдущем разделе мы построили универсальную функцию для класса всех вычислимых функций одного аргумента. Можно ли сделать то же самое для класса всюду определенных вычислимых функций? Оказывается, что нет.
Теорема 8.Не существует вычислимой всюду определенной функции двух аргументов, универсальной для класса всех вычислимых всюду определенных функций одного аргумента.
Воспользуемся "диагональной конструкцией" точно так же доказывается несчетность множества всех бесконечных десятичных дробей. Пусть U произвольная вычислимая всюду определенная функция двух аргументов. Рассмотрим диагональную функцию u(n) = U(n,n). Очевидно, на аргументе n функция u совпадает с функцией Un, а функция d(n) = u(n) + 1 отличается от Un. Таким образом, вычислимая всюду определенная функция d(n) отличается от всех сечений Un, и потому функция U не является универсальной.
Почему это рассуждение не проходит для класса всех вычислимых функций (в том числе частичных)? Дело в том, что значение d(n) = U(n,n) + 1 теперь не обязано отличаться от значения Un(n) = U(n,n), так как оба они могут быть не определены.
Тем не менее, часть рассуждения остается в силе.
Теорема 9.Существует вычислимая функция d (с натуральными аргументами и значениями), от которой никакая вычислимая функция f не может всюду отличаться: для любой вычислимой функции f найдется такое число n, что f(n) = d(n) (последнее равенство понимается в том смысле, что либо оба значения f(n) и d(n) не определены, либо оба определены и равны).
По существу все уже сказано: такова диагональная функция d(n) = U(n,n) (здесь U вычислимая функция двух аргументов, универсальная для класса вычислимых функций одного аргумента). Любая вычислимая функция f есть Un при некотором n и потому f(n) = Un(n) = U(n,n) = d(n).
Теорема 10.Существует вычислимая функция, не имеющая всюду определенного вычислимого продолжения.
Такова, например, функция d'(n) = d(n) + 1, где d функция из предыдущей теоремы. В самом деле, любое ее всюду определенное продолжение всюду отличается от d (в тех местах, где функция d определена, функция d' на единицу больше d и потому любое продолжение функции d' отличается от d ; там, где d не определена, любая всюду определенная функция отличается от d ).
19. Докажите, что и сама функция d из доказательства предыдущей теоремы не имеет вычислимого всюду определенного продолжения.
