Нумерации и операции

Главные универсальные функции

Очевидно, композиция двух вычислимых функций вычислима. При этом это утверждение кажется "эффективным" в том смысле, что по программам двух функций можно алгоритмически получить программу их композиции. В разумном языке программирования она будет состоять из двух подпрограмм, соответствующих двум вычислимым функциям, и главной программы с единственной строкой " return (f(g(x))) ".

Однако мы хотим говорить не о программах (чтобы не вдаваться в детали языка программирования), а о номерах функций. Для этого у нас есть средства. Именно, всякая универсальная функция U для класса вычислимых функций одного аргумента задает нумерацию этого класса: число n является номером функции .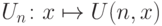

Вообще нумерацией (более точно, натуральной нумерацией ) произвольного множества F называют всюду определенное отображение u : N -> F, область значений которого есть все множество F. Если v(n) = f, то число n называют номером объекта f. Таким образом, всякая функция двух аргументов задает нумерацию некоторого класса функций одного аргумента (и является универсальной для этого класса).

Наша цель сформулировать и доказать такое утверждение: (при некоторых условиях на нумерацию вычислимых функций) существует алгоритм, который по любым двум номерам вычислимых функций дает некоторый номер их композиции.

Прежде всего мы потребуем, чтобы универсальная функция, задающая нумерацию, была вычислимой. (Такие нумерации называют вычислимыми.) Однако этого условия мало: нам потребуется, чтобы нумерация была, как говорят, главной ( геделевой ).

Пусть U двуместная вычислимая универсальная функция для класса одноместных вычислимых функций (термин " k -местная функция" означает " функция k аргументов"). Ее называют главной универсальной функцией, если для любой двуместной вычислимой функции V существует всюду определенная вычислимая функция s(m), для которой

V(m,x) = U(s(m),x)

при всех m и x (равенство понимается, как обычно, в том смысле, что либо оба значения не определены, либо определены и равны).

Другими словами, V_m = U_s(m), то есть функция s дает по V -номеру некоторой функции некоторый U -номер той же функции.

Теорема 15. Существует главная универсальная функция.

(Первый способ.) Покажем, что описанное в доказательстве теоремы 6 построение универсальной функции дает главную универсальную функцию. Напомним, что мы перечисляли все программы p₀,p₁,p₂, ... какого-то естественного языка программирования в порядке возрастания их длин и полагали U(n,x) равным результату применения программы p_n к входу x. Пусть теперь есть какая-то другая вычислимая функция V двух аргументов. Нам надо по любому натуральному m получить программу функции V_m, то есть функции, которая получится, если в V зафиксировать первый аргумент равным m. Ясно, что такую программу (в большинстве языков программирования) получить легко надо только в программе для V заменить первый аргумент на определение константы (или использовать программу для V в качестве подпрограммы, а в основной программе вызывать V с фиксированным первым аргументом).

(Второй способ.) Но можно и не вдаваться в детали построения универсальной функции, а воспользоваться лишь фактом ее существования.

Заметим сначала, что существует вычислимая функция трех аргументов, универсальная для класса вычислимых функций двух аргументов, то есть такая функция T, что при фиксации первого аргумента среди функций T_n(u,v) = T(n,u,v) встречаются все вычислимые функции двух аргументов.

Такую функцию можно построить так. Фиксируем некоторую вычислимую нумерацию пар, то есть вычислимое взаимно однозначное соответствие между N x N и N ; число [u,v], соответствующее паре 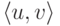, мы будем называть номером этой пары. Если теперь R двуместная вычислимая универсальная функция для вычислимых одноместных функций, то вычислимая функция T, определенная формулой T(n,u,v) = R(n,[u,v]), будет универсальной для вычислимых двуместных функций. В самом деле, пусть F произвольная вычислимая функция двух аргументов. Рассмотрим вычислимую одноместную функцию f, определенную соотношением f([u,v]) = F(u,v). Поскольку R универсальна, найдется число n, для которого R(n,x) = f(x) при всех x. Для этого n выполнены равенства T(n,u,v) = R(n,[u,v]) = f([u,v]) = F(u,v), и потому n -ое сечение функции T совпадает с F. Итак, универсальная функция трех аргументов построена.

Теперь используем ее для определения главной универсальной функции U двух аргументов. Неформально говоря, мы встроим внутрь U все другие вычислимые функции двух аргументов, и тем самым U станет главной. Формально говоря, положим U([n,u],v) = T(n,u,v) и проверим, что функция U будет главной. Любая вычислимая функция V двух аргументов встречается среди сечений функции T: можно найти такое n, что V(u,v) = T(n,u,v) для всех u и v. Тогда V(u,v) = U([n,u],v) для всех u и v и потому функция s, определенная формулой s(u) = [n,u], удовлетворяет требованиям из определения главной универсальной функции.

Нумерации, соответствующие главным универсальным функциям, называют главными, или геделевыми.

Теперь уже можно доказать точный вариант утверждения, с которого мы начали.

Теорема 16. Пусть U двуместная главная универсальная функция для класса вычислимых функций одного аргумента. Тогда существует всюду определенная функция c, которая по номерам p и q двух функций одного аргумента дает номер c(p,q) их композиции: U_c(p,q) есть композиция , то есть

U(c(p,q),x) = U(p, U(q,x))

для всех p, q и x.

Рассмотрим двуместную вычислимую функцию V, для которой V([p,q],x) = U(p,U(q,x)). По определению главной универсальной функции, найдется такая всюду определенная одноместная вычислимая функция s, что V(m,x) = U(s(m),x) для всех m и x. Тогда V([p,q],x) = U(s([p,q]),x) и потому функция c, определенная соотношением c(p,q) = s([p,q]), будет искомой.

Повторим это доказательство неформально. Определение главной универсальной функции требует, чтобы для любого другого языка программирования, для которого имеется вычислимый интерпретатор V, существовал бы вычислимый транслятор s программ этого языка в программы языка U. (Для краткости мы не различаем программы и их номера и рассматриваем число m как U -программу функции U_m.)

Теперь рассмотрим новый способ программирования, при котором пара 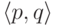объявляется программой композиции функций с U -программами p и q. По условию, такие программы можно алгоритмически транслировать в U -программы, что и требовалось доказать.

Любопытно, что верно и обратное к теореме 16 утверждение:

  28. Пусть U двуместная вычислимая универсальная функция для класса вычислимых функций одного аргумента. Если существует всюду определенная функция, которая по номерам p и q двух функций одного аргумента дает какой-либо номер их композиции, то функция U является главной. (Указание: покажите, что по k можно алгоритмически получать U -номер функции .)

Естественный вопрос: существуют ли вычислимые универсальные функции, не являющиеся главными? Мы увидим дальше, что существуют.

  29. Изменим определение главной универсальной функции и будем требовать существования " транслятора" s лишь для универсальных вычислимых функций V (а не для любых, как раньше). Покажите, что новое определение эквивалентно старому. (Указание: любую функцию можно искусственно переделать в универсальную, " растворив" в ней любую другую универсальную функцию.)

  30. Пусть U главная универсальная функция. Докажите, что для любой вычислимой функции V(m,n,x) существует такая всюду определенная вычислимая функция s(m,n), что V(m,n,x) = U(s(m,n),x) при всех m, n и x. (Указание: объединить m и n в пару.)