Основы теории вычислимых функций
[+]
Опубликован: 16.03.2007 | Доступ: свободный | Студентов: 532 / 43 | Оценка: 4.45 / 4.18 | Длительность: 15:50:00
Тема: Алгоритмы и дискретные структуры
Специальности: Программист, Математик
Теги: beta, алгоритмы, всюду определенные функции, вычисления, вычислимость, вычислительная модель, графика, дополнение множества, одноместная функция, полугруппа, примитивная рекурсия, примитивно рекурсивная функция, процедуры, разрешимые множества, теория, универсальное множество, частично рекурсивная функция, элементы, эффективность
Лекция 3:

Нумерации и операции
A
|
версия для печати
< Лекция 2 || Лекция 3: 12 || Лекция 4 >

Вычислимые последовательности функций

Пусть дана некоторая последовательность f0,f1, ... вычислимых функций одного аргумента. Мы хотим придать смысл выражению " последовательность i\mapsto f_i вычислима". Это можно сделать двумя способами:

  • можно называть эту последовательность вычислимой, если функция F двух аргументов, заданная формулой F(i,n) = fi(n), является вычислимой.
  • можно называть эту последовательность вычислимой, если существует вычислимая последовательность чисел c0,c1, ..., для которой ci является одним из номеров функции fi.

Второе определение (в отличие от первого) зависит от выбора нумерации.

Теорема 17. Если нумерация является вычислимой (то есть соответствующая универсальная функция вычислима), то из второго определения следует первое. Если нумерация является к тому же главной, то из первого определения следует второе.

(Впредь, говоря о вычислимой последовательности вычислимых функций, мы будем всегда предполагать, что нумерация является главной, так что можно пользоваться любым из двух определений.)

Если U вычислимая универсальная функция, а последовательность i\hm\mapsto c_i вычислима, то функция F\colon \langle i,x\rangle\hm\mapsto f_i(x)\hm=U(c_i,x) вычислима как результат подстановки одной вычислимой функции в другую.

Напротив, если функция F вычислима, а универсальная функция U является главной, то функция-транслятор, существующая по определению главной универсальной функции, как раз и дает по i один из номеров функции fi.

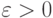  31. Пусть фиксирована главная универсальная функция для класса вычислимых функций одного аргумента. Тогда возникает нумерация вычислимых действительных чисел в соответствии с определением: номером числа \alpha является любой номер любой функции, которая по рациональному \varepsilon > 0 дает \varepsilon -приближение к \alpha.

  • Покажите, что существует алгоритм, который по любым двум номерам двух вычислимых действительных чисел дает (некоторый) номер их суммы.
  • Покажите, что не существует алгоритма, который по любому номеру любого вычислимого действительного числа отвечает на вопрос, равно ли это число нулю.
  • Как мы видели в задаче 14, всякое вычислимое действительное число имеет вычислимое десятичное разложение. Покажите, что тем не менее нет алгоритма, который по любому номеру любого вычислимого действительного числа дает номер вычислимой функции, задающей его десятичное разложение.

Главные универсальные множества

По аналогии с функциями, перечислимое множество W \subset N \times N называется главным универсальным перечислимым множеством (для класса всех перечислимых подмножеств N ), если для любого другого перечислимого множества V \subset N \times N найдется такая всюду определенная вычислимая функция s : N -> N, что

\langle n,x\rangle \in V \Leftrightarrow \langle s(n),x\rangle \in W

для всех n и x. (Очевидно, что из этого свойства следует универсальность.)

Как и для функций, можно перейти к нумерациям. Каждое множество U \subset N \times N задает нумерацию некоторого семейства подмножеств натурального ряда: число n является номером n -го сечения U_n=\{x\mid \langle n,x\rangle\in U\}. Перечислимое подмножество множества N x N задает нумерацию некоторого семейства перечислимых подмножеств натурального ряда; такие нумерации называют вычислимыми. Перечислимое множество W \subset N \times N универсально, если и только если всякое перечислимое подмножество натурального ряда имеет W -номер; оно является главным тогда и только тогда, когда любая вычислимая нумерация V (любого семейства перечислимых множеств) вычислимо сводится к W -нумерации в том смысле, что Vn = Ws(n) для некоторой вычислимой функции s и для всех n.

Теорема 18. Существует главное универсальное перечислимое множество W \subset N \times N.

Эта теорема является очевидным следствием такого утверждения:

Область определения главной универсальной функции для класса вычислимых функций одного аргумента является главным универсальным множеством для класса перечислимых подмножеств N.

Доказательство леммы. Пусть U главная универсальная функция, а W область ее определения. Пусть V \subset N \times N произвольное перечислимое множество. Рассмотрим вычислимую функцию G с областью определения V. Поскольку функция U является главной, найдется всюду определенная вычислимая функция s : N -> N, для которой Gn = Us(n) при всех n. Тогда равны и области определения функций Gn и Us(n), то есть Vn = Ws(n).

  32. Постройте главное универсальное множество непосредственно, используя универсальное подмножество N3 (по аналогии с выше приведенным построением главной универсальной функции).

Как и для функций, мы теперь можем доказывать, что различным операциям над множествами соответствуют вычислимые преобразования номеров. Вот лишь один пример такого рода:

Теорема 19. Пусть W \subset N \times N главное универсальное перечислимое множество. Тогда по W -номерам двух перечислимых множеств можно алгоритмически получить номер их пересечения: существует такая вычислимая всюду определенная функция двух аргументов s, что

W_{s(m,n)} = W_{m} \cap W_{n}

для любых двух m и n.

Рассмотрим множество V \subset N \times N, определенное так:

\langle [m,n], x\rangle \in V \Leftrightarrow x \in (W_m \cap W_n)

(здесь квадратные скобки обозначают номер пары) и применим к нему определение главного универсального множества.

Как и для функций, понятие вычислимости последовательности перечислимых множеств может быть определено двояко: можно считать вычислимой последовательность V0,V1, ... сечений произвольного перечислимого множества V, а можно требовать, чтобы по i можно было алгоритмически указать один из номеров i -го члена последовательности в главной нумерации. Эти определения равносильны (доказательство полностью аналогично рассуждению для функций).

Дальше >>
< Лекция 2 || Лекция 3: 12 || Лекция 4 >

Вопросы и ответы

вопросов: 0