m-сводимость и свойства перечислимых множеств
m-полнота и эффективная неперечислимость
Теория алгоритмов позволяет, как говорят, "конструктивизировать" различные определения. В качестве примера возьмем определение бесконечного множества. Что такое бесконечное множество? Это множество, которое содержит не менее n элементов для любого натурального n. Теперь можно сказать так: множество называется " эффективно бесконечным", если существует алгоритм, который по любому n указывает n различных элементов этого множества.
48. Покажите, что произвольное множество A является эффективно бесконечным тогда и только тогда, когда оно содержит бесконечное перечислимое множество (е бесконечно, но не является иммунным).
Сейчас нас будет интересовать эффективный вариант понятия неперечислимости. Что значит, что множество A неперечислимо? Это означает (трюизм), что A отличается от любого перечислимого множества. Естественно называть множество A эффективно неперечислимым, если по любому перечислимому множеству можно указать место, где оно отличается от A.
Более формально, зафиксируем некоторое главное универсальное
перечислимое множество W (и тем самым нумерацию перечислимых
множеств: число n мы считаем номером
множества Wn ). Будем
говорить, что множество A является эффективно неперечислимым, если существует
такая всюду определенная
вычислимая функция f, что 
 Wz при
всех z. (Здесь
Wz при
всех z. (Здесь  означает симметрическую
разность; другими словами, f(z) является точкой, где A отличается от Wz.)
означает симметрическую
разность; другими словами, f(z) является точкой, где A отличается от Wz.)
Заметим, что это свойство не зависит от выбора главного универсального множества, так как от номеров относительно одного такого множества можно эффективно переходить к номерам относительно другого.
Свойство эффективной неперечислимости допускает простую характеризацию в терминах m -сводимости. Начнем с такого простого наблюдения.
Теорема 34. Если A <=m B и A эффективно неперечислимо, то и B эффективно неперечислимо.
Эта теорема является "эффективным вариантом" теоремы 31, часть (б). То же самое можно сказать и о ее доказательстве. Пусть мы хотим найти точку, в которой B отличается от некоторого перечислимого множества X. Рассмотрим функцию f, которая m -сводит A к B. Прообраз f-1(X) перечислимого множества X при вычислимом отображении будет перечислим, поэтому можно найти точку m, в которой он отличается от A. Тогда B отличается от X в точке f(m).
Чтобы сделать это рассуждение точным, нам нужно лишь доказать, что номер перечислимого множества f-1(X) может быть эффективно получен по номеру перечислимого множества X. Для этого мы должны воспользоваться тем, что нумерация является главной схема тут та же, что и при вычислении номера композиции двух вычислимых функций, заданных своими номерами (теорема 16). Проведем это рассуждение подробно.
Рассмотрим перечислимое множество

(оно перечислимо, поскольку является прообразом перечислимого
множества W при вычислимом отображении 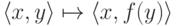 ). Легко видеть, что Vn =
f-1(Wn). Так как множество W является главным
универсальным множеством, то существует вычислимая всюду
определенная функция s, для которой Ws(n)=Vn=f-1(Wn)
при всех n. Другими словами, функция s по W -номеру любого
перечислимого множества дает W -номер его прообраза при
отображении f, что и требовалось.
). Легко видеть, что Vn =
f-1(Wn). Так как множество W является главным
универсальным множеством, то существует вычислимая всюду
определенная функция s, для которой Ws(n)=Vn=f-1(Wn)
при всех n. Другими словами, функция s по W -номеру любого
перечислимого множества дает W -номер его прообраза при
отображении f, что и требовалось.
Теорема 35. Существуют перечислимые множества с эффективно неперечислимыми дополнениями.
Вновь рассмотрим диагональное множество 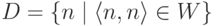 . Его дополнение будет эффективно неперечислимым. В
самом деле, множества Wn и D одинаково себя ведут в
точке n, поэтому Wn отличается от дополнения
к D в этой точке.
Таким образом, дополнение к D эффективно неперечислимо, причем
в качестве функции f из определения эффективной
неперечислимости можно взять тождественную функцию.
. Его дополнение будет эффективно неперечислимым. В
самом деле, множества Wn и D одинаково себя ведут в
точке n, поэтому Wn отличается от дополнения
к D в этой точке.
Таким образом, дополнение к D эффективно неперечислимо, причем
в качестве функции f из определения эффективной
неперечислимости можно взять тождественную функцию.
Из двух предыдущих теорем очевидно следует такое утверждение:
Теорема 36. Всякое m -полное перечислимое множество имеет эффективно неперечислимое дополнение.
На самом деле верно и обратное. Чтобы убедиться в этом, докажем такой факт:
Теорема 37. Пусть K перечислимое множество, а A эффективно неперечислимо. Тогда N \ K <=m A (или, что эквивалентно, K <=m N \ A ).
На самом деле нам важно умение эффективно отличать A лишь от
двух перечислимых множеств от пустого и от всего
натурального ряда. Отличить A от пустого множества означает
указать элемент в A ; отличить от всего натурального ряда
означает указать элемент вне A. Именно эти две вещи используются
при сведении. Более формально, рассмотрим
множество V=K x N. Его сечения Vn либо
пусты
(при 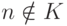 ), либо совпадают со всем натуральным рядом
(при
), либо совпадают со всем натуральным рядом
(при 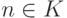 ). Пользуясь тем, что множество W
является главным, мы
находим всюду определенную функцию s, для
которой
). Пользуясь тем, что множество W
является главным, мы
находим всюду определенную функцию s, для
которой 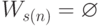 при
при 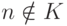 и Ws(n)=N
при
и Ws(n)=N
при 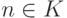 . Пусть f функция, обеспечивающая
эффективную
неперечислимость множества A. Тогда
. Пусть f функция, обеспечивающая
эффективную
неперечислимость множества A. Тогда 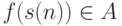 при
при 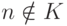 и
и 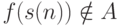 при
при 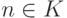 . Другими словами,
композиция функций f и s сводит N \ K к
множеству A, что и требовалось.
. Другими словами,
композиция функций f и s сводит N \ K к
множеству A, что и требовалось.
Отсюда очевидно вытекают такие утверждения:
Теорема 38. Перечислимое множество является m -полным тогда и только тогда, когда его дополнение эффективно неперечислимо.
Теорема 39. Множество эффективно неперечислимо тогда и только тогда, когда к нему m -сводится дополнение некоторого (вариант: любого) m -полного множества.
Отметим, что не всякое неперечислимое множество эффективно неперечислимо. Это видно, например, из такого факта:
Теорема 40. Любое эффективно неперечислимое множество содержит бесконечное перечислимое подмножество (е не является иммунным).
В самом деле, пусть множество A эффективно неперечислимо. Тогда отличим его от пустого множества то есть найдем в нем элемент. После этого отличим его от одноэлементного множества, которое состоит из этого элемента и найдем другой элемент. Действуя так, мы может алгоритмически найти сколь угодно много различных элементов.
В этом рассуждении мы использовали такой факт: по конечному множеству, заданному списком его элементов, можно получить его номер (точнее, один из номеров) в главной нумерации перечислимых множеств. Почему это так? Пусть фиксирована некоторая вычислимая нумерация конечных множеств. Будем обозначать n -ое конечное множество в этой нумерации через Dn. Тогда Dn будет n -ым сечением перечислимого (и даже разрешимого) множества

Остается воспользоваться определением главной нумерации перечислимых множеств.
Простые множества, которые, как мы знаем, существуют (теорема 14), являются примерами перечислимых множеств, не являющихся m -полными. Именно так и возникло понятие простого множества: Пост искал пример перечислимого неразрешимого множества, которое не было бы m -полным.
