Базовые операции обработки изображений

2.8. Выравнивание гистограмм

Существует три основных метода повышения контраста изображения:

1. линейная растяжка гистограммы (линейное контрастирование),
2. нормализация гистограммы,
3. выравнивание (линеаризация или эквализация, equalization) гистограммы.

Линейная растяжка сводится к присваиванию новых значений интенсивности каждому пикселю изображения. Если интенсивности исходного изображения изменялись в диапазоне от 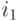до 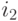, тогда необходимо линейно "растянуть" указанный диапазон так, чтобы значения изменялись от 0 до 255. Для этого достаточно пересчитать старые значения интенсивности 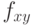для всех пикселей (x,y) согласно формуле 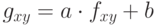, где коэффициенты a,b просто вычисляются, исходя из того, что граница 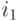должна перейти в 0, а 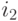– в 255.

Нормализация гистограммы в отличие от предыдущего метода обеспечивает растяжку не всего диапазона изменения интенсивностей, а только его наиболее информативной части. Под информативной частью понимается набор пиков гистограммы, т.е. интенсивности, которые чаще остальных встречаются на изображении. Бины, соответствующие редко встречающимся интенсивностям, в процессе нормализации отбрасываются, далее выполняется обычная линейная растяжка получившейся гистограммы.

Выравнивание гистограмм – это один из наиболее распространенных способов. Цель выравнивания состоит в том, чтобы все уровни яркости имели бы одинаковую частоту, а гистограмма соответствовала равномерному закону распределения. Допустим, что задано изображение в оттенках серого, которое имеет разрешение пикселей. Количество уровней квантования яркости пикселей (число бинов) составляет . Тогда в среднем на каждый уровень яркости должно выпадать пикселей. Базовая математика лежит в сопоставлении двух распределений. Пусть x,y – случайные величины, описывающие изменение интенсивности пикселей на изображениях, 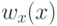– плотность распределения интенсивности на исходном изображении, 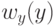– желаемая плотность распределения. Необходимо найти преобразование плотностей распределения 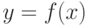, которое позволило бы получить желаемую плотность:

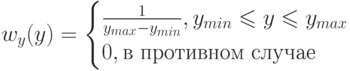
Обозначим через и 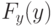интегральные законы распределения случайных величин x и y. Из условия вероятностной эквивалентности следует, что 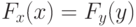. Распишем интегральный закон распределения по определению:

Отсюда получаем, что

Осталось выяснить, как оценить интегральный закон распределения . Для этого необходимо сначала построить гистограмму исходного изображения, затем нормализовать полученную гистограмму, разделив величину каждого бина на общее количество пикселей 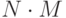. Значения бинов можно рассматривать как приближенное значение функции плотности распределения 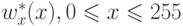. Таким образом, значение интегральной функции распределения можно представить как сумму следующего вида:

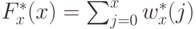
Построенную оценку можно использовать для вычисления новых значений интенсивности. Заметим, что перечисленные преобразования гистограмм можно применять не только ко всему изображению, но и к отдельным его частям.

В библиотеке OpenCV реализована функция equalizeHist, которая обеспечивает повышение контрастности изображения посредством выравнивания гистограммы [1, 7]. Прототип функции показан ниже.

void equalizeHist(const Mat&src, Mat&dst) 

Функция работает в четыре этапа:

1. Вычисление гистограммы H исходного изображения src. Отметим, что src – 8-битное одноканальное изображение.
2. Нормализация гистограммы. Нормализация посредством деления величины каждого бина гистограммы на общее количество пикселей.
3. Построение интегральной гистограммы .
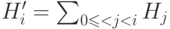4. Определение нового значения интенсивности пикселя dst(x,y) = H'(src(x,y)).

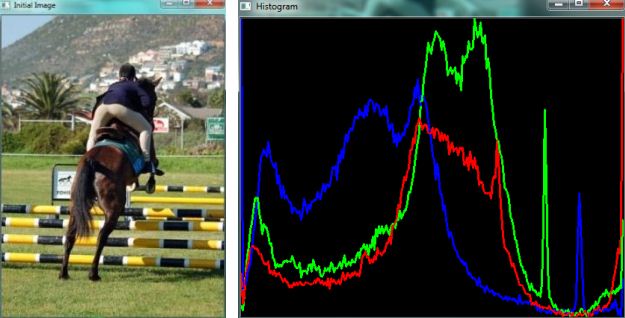
Далее приведем пример программы, обеспечивающей выравнивание гистограммы. Приложение принимает в качестве аргумента командной строки название исходного изображения. После выполнения операции выравнивания гистограммы выполняется отображение исходного изображения^{1Использовано изображение, входящее в состав базы PASACL VOC 2007.} , переведенного в оттенки серого (рис.9.11, слева), и изображения с выровненной гистограммой (рис.9.11, справа).

#include <stdio.h> 
#include <opencv2/opencv.hpp> 
 
using namespace cv; 
 
const char helper[] =  
    "Sample_equalizeHist.exe  <img_file>\n\ 
    \t<img_file> - image file name\n"; 
                                                       
1
  
int main(int argc, char* argv[]) 
{ 
    const char *initialWinName = "Initial Image", 
               *equalizedWinName = "Equalized Image"; 
    Mat img, grayImg, equalizedImg; 
    if (argc < 2) 
    { 
        printf("%s", helper); 
        return 1; 
    }     
    // загрузка изображения 
    img = imread(argv[1], 1); 
    // преобразование в оттенки серого 
    cvtColor(img, grayImg, CV_RGB2GRAY); 
    // выравнивание гистограммы 
    equalizeHist(grayImg, equalizedImg); 
 
    // отображение исходного изображения и гистограмм 
    namedWindow(initialWinName, CV_WINDOW_AUTOSIZE); 
    namedWindow(equalizedWinName, CV_WINDOW_AUTOSIZE); 
    imshow(initialWinName, grayImg); 
    imshow(equalizedWinName, equalizedImg); 
    waitKey(); 
     
    // закрытие окон 
    destroyAllWindows(); 
    // осовобождение памяти 
    img.release(); 
    grayImg.release(); 
    equalizedImg.release(); 
    return 0; 
}    

Рис. 9.11. Результат выравнивания гистограммы