|
Нахожу в тесте вопросы, которые в принципе не освещаются в лекции. Нужно гуглить на других ресурсах, чтобы решить тест, или же он всё же должен испытывать знания, полученные в ходе лекции? |
Базовые операции обработки изображений
2.6. Детектор ребер Канни
Детектор ребер Канни [4, 8, 9] предназначен для поиска границ объектов на изображении. Детектор строится на основании оператора Собеля и включает несколько этапов:
- Удаление шума на изображении посредством применения фильтра
Гаусса с ядром размера 5:
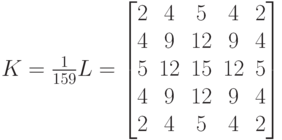
- Вычисление первых производных (магнитуд и направлений) функции
интенсивности пикселей по горизонтальному и вертикальному
направлениям посредством применения оператора Собеля с ядрами
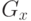 и
и  (см. раздел 2.4). Направления градиентов округляются до одного
из возможных значений
(см. раздел 2.4). Направления градиентов округляются до одного
из возможных значений  ,
, ,
, ,
, .
. - Отбор пикселей, которые потенциально принадлежат ребру с использованием процедуры non-maximum suppression [4]. Пиксели, которым соответствуют вектора производных по направлениям, являющиеся локальными максимумами, считаются потенциальными кандидатами на принадлежность ребру.
- Двойное отсечение (гистерезис). Выделяются "сильные" и "слабые" ребра. Пиксели, интенсивность которых превышает максимальный порог, считаются пикселями, принадлежащими "сильным" ребрам. Принимается, что пиксели с интенсивностью, входящей в интервал от минимального до максимального порогового значения, принадлежат "слабым" ребрам. Пиксели, интенсивность которых меньше минимального порога, отбрасываются из дальнейшего рассмотрения. Результирующие ребра содержат пиксели всех "сильных" ребер и те пиксели "слабых" ребер, чья окрестность содержит хотя бы один пиксель "сильных" ребер.
Детектор Канни реализован в библиотеке OpenCV [7] в виде отдельной функции, прототип которой приведен далее.
void Canny(const Mat&image, Mat&edges, double threshold1,
double threshold2, int apertureSize=3,
bool L2gradient=false)
Функция принимает на вход следующие параметры:
- image – одноканальное 8-битное изображение.
- edges – результирующая карта ребер, представляется матрицей, размер которой совпадает с размером исходного изображения.
- threshold1, threshold2 – параметры алгоритма, пороговые значения для отсечения.
- apertureSize – размер апертуры для применения оператора Собеля.
-
L2gradient – флаг, который указывает, по какой норме будет
вычисляться магнитуда градиента. Принимает истинное значение,
если используется норма
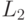 (корень квадратный из суммы
квадратов частных производных), в противном случае
(корень квадратный из суммы
квадратов частных производных), в противном случае 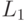 (сумма
модулей частных производных). Как правило, нормы
(сумма
модулей частных производных). Как правило, нормы 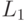 достаточно, и вычисляется она быстрее в связи с отсутствием
вызова функции sqrt.
достаточно, и вычисляется она быстрее в связи с отсутствием
вызова функции sqrt.
Приведем пример использования детектора Канни. Отметим, что перед непосредственным применением детектора выполняется размытие изображения (blur) и преобразование в оттенки серого (cvtColor).
#include <stdio.h>
#include <opencv2/opencv.hpp>
using namespace cv;
const char helper[] =
"Sample_Canny.exe <img_file>\n\
\t<img_file> - image file name\n";
int main(int argc, char* argv[])
{ const char *cannyWinName = "Canny detector";
Mat img, grayImg, edgesImg;
double lowThreshold = 70, uppThreshold = 260;
if (argc < 2)
{
printf("%s", helper);
return 1;
}
// загрузка изображения
img = imread(argv[1], 1);
// удаление шумов
blur(img, img, Size(3,3));
// преобразование в оттенки серого
cvtColor(img, grayImg, CV_RGB2GRAY);
// применение детектора Канни
Canny(grayImg, edgesImg, lowThreshold, uppThreshold);
// отображение результата
namedWindow(cannyWinName, CV_WINDOW_AUTOSIZE);
imshow(cannyWinName, edgesImg);
waitKey();
// закрытие окон
destroyAllWindows();
// осовобождение памяти
img.release();
grayImg.release();
edgesImg.release();
return 0;
}
На рисунке (рис.9.9) показан результат применения детектора Канни к тестовому изображению (рис.9.2, слева).
2.7. Вычисление гистограмм
Один из наиболее распространенных дефектов фотографических, сканерных и телевизионных изображений – слабый контраст. Дефект во многом обусловлен ограниченностью диапазона воспроизводимых яркостей. Под контрастом понимается разность максимального и минимального значений яркости. Контрастность изображения можно повысить за счет изменения яркости каждого элемента изображения и увеличения диапазона яркостей. Существует несколько методов, основанных на вычислении гистограммы.
Допустим, что имеется изображение в оттенках серого, интенсивность
пикселей которого изменяется в пределах значений от a до b , где  и
и
 . Для изображения можно построить гистограмму со столбцами,
отвечающими количеству пикселей определенной интенсивности. Такого
рода гистограмма позволяет представить распределение оттенков на
изображении. В общем случае под гистограммой понимается коллекция
целочисленных значений, каждое из которых определяет количество точек,
обладающих некоторым свойством или принадлежащих определенному
бину. На практике гистограммы применяются, чтобы получить
статистическую картину о распределении каких-либо данных (пикселей,
векторов признаков, направлений градиента во всех точках изображения и
т.п.).
. Для изображения можно построить гистограмму со столбцами,
отвечающими количеству пикселей определенной интенсивности. Такого
рода гистограмма позволяет представить распределение оттенков на
изображении. В общем случае под гистограммой понимается коллекция
целочисленных значений, каждое из которых определяет количество точек,
обладающих некоторым свойством или принадлежащих определенному
бину. На практике гистограммы применяются, чтобы получить
статистическую картину о распределении каких-либо данных (пикселей,
векторов признаков, направлений градиента во всех точках изображения и
т.п.).
В данном разделе остановимся на рассмотрении структур данных и функций OpenCV, обеспечивающих вычисление гистограмм. Ниже приведены прототипы доступных функций.
void calcHist(const Mat* arrays, int narrays, const int* channels, const Mat&mask,
MatND& hist, int dims, const int* histSize,
const float** ranges, bool uniform=true,
bool accumulate=false)
void calcHist(const Mat* arrays, int narrays,
const int* channels, const Mat&mask,
SparseMat&hist, int dims,
const int* histSize, const float** ranges,
bool uniform=true, bool accumulate=false)
Параметры:
- arrays – исходные массивы данных или изображения. Должны иметь одинаковую глубину (CV_8U или CV_32F) и размер.
- narrays – количество исходных массивов данных.
- channels – массив индексов каналов в каждом входном массиве, по которым будет вычисляться гистограмма.
- mask – маска, на которой считается гистограмма. Опциональный параметр. Если маска не пуста, то она представляется 8-битной матрицей того же размера, что и каждый исходный массив. При построении гистограммы учитываются только элементы массивов, которые соответствуют ненулевым элементам маски. Если маска пуста, то построение гистограммы выполняется на полном наборе данных.
- hist – результирующая гистограмма, плотная в случае использования первого прототипа функции, разреженная – в случае второго. Для хранения плотной гистограммы используется структура данных MatND, для разреженной – SparseMat. MatND представляется в виде n-мерного массива, SparseMat – хэш- таблицей ненулевых значений [10].
- dims – размерность гистограммы. Параметр принимает положительные целочисленные значения, не превышающие CV_MAX_DIMS = 32.
- histSize – количество бинов по каждой размерности гистограммы.
- ranges – интервалы изменения значений по каждой размерности гистограммы. Если гистограмма равномерная (uniform = true), то для любой размерности i достаточно указать только нижнюю границу изменения (по существу значение, соответствующее первому бину), верхняя граница будет совпадать с histSize[i]- 1.
- uniform – флаг, который определяет тип диаграммы (равномерная или нет).
- accumulate – флаг, указывающий на необходимость очищения гистограммы перед непосредственными вычислениями. Использование данного флага позволяет использовать одну и ту же гистограмму для нескольких множеств массивов или обновлять гистограмму во времени.
Рассмотрим пример программы, которая осуществляет построение и отображение гистограмм по каждому каналу цветного изображения. Программа получает в качестве аргументов командной строки название изображения, расщепляет полученную матрицу по каналам (split) и вычисляет гистограмму для каждого канала изображения (calcHist). Заметим, что в OpenCV каналы изображения хранятся в порядке BGR, а не в RGB. Далее выполняется нормализация гистограмм (normalize) для приемлемого отображения в виде ломаных.
#include <stdio.h>
#include <opencv2/opencv.hpp>
using namespace cv;
const char helper[] =
"Sample_calcHist.exe <img_file>\n\
\t<img_file> - image file name\n";
int main(int argc, char* argv[])
{
const char *initialWinName = "Initial Image",
*histWinName = "Histogram";
Mat img, bgrChannels[3], bHist, gHist, rHist, histImg;
int kBins = 256; // количество бинов гистограммы
// интервал изменения значений бинов
float range[] = {0.0f, 256.0f};
const float* histRange = { range };
// равномерное распределение интервала по бинам
bool uniform = true;
// запрет очищения перед вычислением гистограммы
bool accumulate = false;
// размеры для отображения гистограммы
int histWidth = 512, histHeight = 400;
// количество пикселей на бин
int binWidth = cvRound((double)histWidth / kBins);
int i, kChannels = 3;
Scalar colors[] = {Scalar(255, 0, 0),
Scalar(0, 255, 0), Scalar(0, 0, 255)};
if (argc < 2)
{ printf("%s", helper);
return 1;
}
// загрузка изображения
img = imread(argv[1], 1);
// выделение каналов изображения
split(img, bgrChannels);
// вычисление гистограммы для каждого канала
calcHist(&bgrChannels[0], 1, 0, Mat(), bHist, 1,
&kBins, &histRange, uniform, accumulate);
calcHist(&bgrChannels[1], 1, 0, Mat(), gHist, 1,
&kBins, &histRange, uniform, accumulate);
calcHist(&bgrChannels[2], 1, 0, Mat(), rHist, 1,
&kBins, &histRange, uniform, accumulate);
// построение гистограммы
histImg = Mat(histHeight, histWidth, CV_8UC3,
Scalar(0, 0, 0));
// нормализация гистограмм в соответствии с размерами
// окна для отображения
normalize(bHist, bHist, 0, histImg.rows,
NORM_MINMAX, -1, Mat());
normalize(gHist, gHist, 0, histImg.rows,
NORM_MINMAX, -1, Mat());
normalize(rHist, rHist, 0, histImg.rows,
NORM_MINMAX, -1, Mat());
// отрисовка ломаных
for (i = 1; i < kBins; i++)
{
line(histImg, Point(binWidth * (i-1),
histHeight-cvRound(bHist.at<float>(i-1))) ,
Point(binWidth * i,
histHeight-cvRound(bHist.at<float>(i)) ),
colors[0], 2, 8, 0);
line(histImg, Point(binWidth * (i-1),
histHeight-cvRound(gHist.at<float>(i-1))) ,
Point(binWidth * i,
histHeight-cvRound(gHist.at<float>(i)) ),
colors[1], 2, 8, 0);
line(histImg, Point(binWidth * (i-1),
histHeight-cvRound(rHist.at<float>(i-1))) ,
Point(binWidth * i,
histHeight-cvRound(rHist.at<float>(i)) ),
colors[2], 2, 8, 0);
}
// отображение исходного изображения и гистограмм
namedWindow(initialWinName, CV_WINDOW_AUTOSIZE);
namedWindow(histWinName, CV_WINDOW_AUTOSIZE);
imshow(initialWinName, img);
imshow(histWinName, histImg); waitKey();
// закрытие окон
destroyAllWindows();
// осовобождение памяти
img.release();
for (i = 0; i < kChannels; i++)
{
bgrChannels[i].release();
}
bHist.release();
gHist.release();
rHist.release();
histImg.release();
return 0;
}
Результат запуска программы на тестовом изображении из набора PASCAL VOC 2007 показан на рисунке (рис.9.10) ниже.




 "
"