|
Нахожу в тесте вопросы, которые в принципе не освещаются в лекции. Нужно гуглить на других ресурсах, чтобы решить тест, или же он всё же должен испытывать знания, полученные в ходе лекции? |
Базовые операции обработки изображений
2.4. Оператор Собеля
Оператор Собеля – дискретный дифференциальный оператор, вычисляющий приближенные значения производных разного порядка для функции яркости пикселей [1]. Наиболее распространенным примером практического использования является определение границ (ребер) объектов на изображении, т.е. точек резкого изменения яркости.
Данный оператор основан на свертке изображения с целочисленными
фильтрами. В простейшем случае оператор построен на вычислении
сверток исходного изображения с ядрами 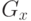 и
и  , обеспечивающими
вычисление первых производных по направлениям:
, обеспечивающими
вычисление первых производных по направлениям:
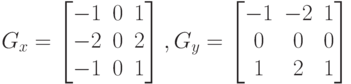
Данный оператор используется для приближенного вычисления градиента
функции интенсивности пикселей. Применение оператора 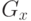 позволяет
определить приближенное значение первой частной производной
изменения интенсивности в горизонтальном направлении,
позволяет
определить приближенное значение первой частной производной
изменения интенсивности в горизонтальном направлении,  – в
вертикальном. На основании данной информации можно вычислить
магнитуду градиента для пикселя с координатами (i,j) согласно формуле
– в
вертикальном. На основании данной информации можно вычислить
магнитуду градиента для пикселя с координатами (i,j) согласно формуле
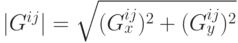 . Также используя полученные данные, можно
определить направление градиента как
. Также используя полученные данные, можно
определить направление градиента как
 .
.
В библиотеке OpenCV поддерживается вычисление первых, вторых, третьих и смешанных производных функции интенсивности пикселей с использованием расширенного оператора Собеля [7]. Ниже приведен прототип соответствующей программной функции.
void Sobel(const Mat&src, Mat&dst, int ddepth,
int xorder, int yorder, int ksize=3,
double scale=1, double delta=0,
int borderType=BORDER_DEFAULT) Перечислим входные параметры функции Sobel:
- src – исходное изображение.
- dst – результирующее изображение.
- ddepth – глубина результирующего изображения.
- xorder – порядок производной по оси Ox.
- yorder – порядок производной по оси Oy.
-
ksize – размер расширенного ядра оператора Собеля. Принимает
одно из значений 1, 3, 5 или 7. Во всех случаях ядро имеет размер
kSize x kSize, кроме ситуации, когда kSize=1. При kSize=1
ядра имеют размер 3x1 или 1x3, по существу применяется фильтр
Гаусса. Указанное значение можно использовать только при
вычислении первых и вторых частных производных по осям Ox и
Oy. По умолчанию ядро имеет размер 3x3. Отметим, что
дополнительно предусмотрено специальное значение параметра
kSize = CV_SCHARR = -1, который соответствует ядру
размера 3x3 фильтра Щарра (Scharr) и может давать более точные
оценки производных по сравнению с оператором Собеля:
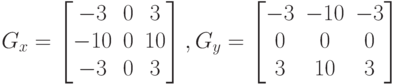
- scale – опциональный параметр, который задает коэффициент масштабирования для вычисляемых значений производных. По умолчанию масштабирование не применяется.
- delta – опциональный параметр смещения интенсивности, добавляется перед сохранением результата в матрицу dst.
- borderType – параметр, определяющий метод дополнения границы.
Далее приведен пример выделения ребер на изображении посредством применения горизонтального и вертикального операторов Собеля и усреднения полученных градиентов по направлениям. Заметим, что предварительно применяется фильтр Гаусса (GaussianBlur) для удаления шумов на исходном изображении и выполняется преобразование полученного изображения в оттенки серого (cvtColor). В результате применения оператора Собеля получаются изображения, глубина которых отличается от глубины исходного изображения, поэтому перед дальнейшими операциями выполняется преобразование указанных матриц в 8-битные целочисленные (convertScaleAbs).
#include <stdio.h>
#include <opencv2/opencv.hpp>
using namespace cv;
const char helper[] =
"Sample_Sobel.exe <img_file>\n\
\t<img_file> - image file name\n";
int main(int argc, char* argv[])
{
const char *initialWinName = "Initial Image",
*xGradWinName = "Gradient in the direction Ox",
*yGradWinName = "Gradient in the direction Oy",
*gradWinName = "Gradient";
int ddepth = CV_16S;
double alpha = 0.5, beta = 0.5;
Mat img, grayImg, xGrad, yGrad,
xGradAbs, yGradAbs, grad;
if (argc < 2)
{
printf("%s", helper);
return 1;
}
// загрузка изображения
img = imread(argv[1], 1);
// сглаживание помощью фильтра Гаусса
GaussianBlur(img, img, Size(3,3),
0, 0, BORDER_DEFAULT);
// преобразование в оттенки серого
cvtColor(img, grayImg, CV_RGB2GRAY);
// вычисление производных по двум направлениям
Sobel(grayImg, xGrad, ddepth, 1, 0); // по Ox
Sobel(grayImg, yGrad, ddepth, 0, 1); // по Oy
// преобразование градиентов в 8-битные
convertScaleAbs(xGrad, xGradAbs);
convertScaleAbs(yGrad, yGradAbs);
// поэлементное вычисление взвешенной
// суммы двух массивов
addWeighted(xGradAbs, alpha, yGradAbs, beta, 0, grad);
// отображение результата
namedWindow(initialWinName, CV_WINDOW_AUTOSIZE);
namedWindow(xGradWinName, CV_WINDOW_AUTOSIZE);
namedWindow(yGradWinName, CV_WINDOW_AUTOSIZE);
namedWindow(gradWinName, CV_WINDOW_AUTOSIZE); imshow(initialWinName, img);
imshow(xGradWinName, xGradAbs);
imshow(yGradWinName, yGradAbs);
imshow(gradWinName, grad);
waitKey();
// закрытие окон
destroyAllWindows();
// осовобождение памяти
img.release();
grayImg.release();
xGrad.release();
yGrad.release();
xGradAbs.release();
yGradAbs.release();
return 0;
}
Ниже на рисунке (рис.9.7) показан результат выполнения приведенной программы на тестовом изображении (рис.9.2, слева).
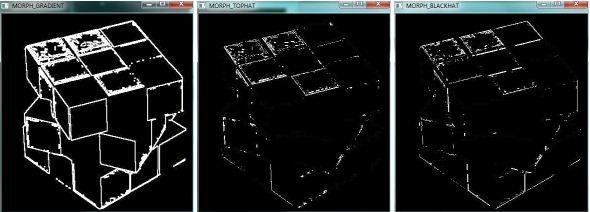
Рис. 9.7. Результат применения оператора Собеля в горизонтальном и вертикальном направлениях, усредненное значение проекций
Очевидно, что применение горизонтального оператора Собеля позволяет отчетливо выделить вертикальные ребра, а вертикального – горизонтальные ребра. Смесь указанных градиентов с весовыми коэффициентами, равными 0.5 обеспечивает вычисление приближенного значения градиента. Для этого используется вызов функции addWeighted.
Отметим, что библиотека OpenCV содержит функцию getDerivKernels, которая позволяет получить ядро для вычисления конкретной частной производной с определенной апертурой. Подробное описание параметров данной функции можно найти в документации [7].
2.5. Оператор Лапласа
Математически оператор Лапласа представляет сумму квадратов
вторых частных производных функции
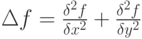 . Дискретный аналог
оператора Лапласа используется при обработке изображений, в частности,
для определения ребер объектов на изображении. Ребра формируются из
множества пикселей, в которых оператор Лапласа принимает нулевые
значения, т.к. нули вторых производных функции соответствуют
экстремальным перепадам интенсивности.
. Дискретный аналог
оператора Лапласа используется при обработке изображений, в частности,
для определения ребер объектов на изображении. Ребра формируются из
множества пикселей, в которых оператор Лапласа принимает нулевые
значения, т.к. нули вторых производных функции соответствуют
экстремальным перепадам интенсивности.
Библиотека OpenCV содержит функцию Laplacian, обеспечивающую вычисление оператора Лапласа [7].
void Laplacian(const Mat&src, Mat&dst, int ddepth,
int ksize=1, double scale=1, double delta=0,
int borderType=BORDER_DEFAULT)
Параметры функции:
- src, dst, ddepth, scale, delta, borderType имеют тот же смысл, что и при вызове функции Sobel.
-
kSize – размер апертуры для вычисление второй производной,
является положительным четным числом. При использовании
значения по умолчанию kSize=1 применяется апертура размером
3x3 и ядро представляется матрицей:
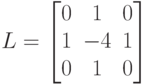
Приведем пример программы, которая обеспечивает поиск ребер объектов на изображения с помощью оператора Лапласа. Перед непосредственным применением оператора выполняется сглаживание с использованием фильтра Гаусса (GaussianBlur) и преобразование исходного изображения в оттенки серого (cvtColor). Заметим, что результирующие значения оператора Лапласа записываются в матрицу, глубина которой аналогично примеру с фильтром Собеля отличается от глубины исходного изображения, поэтому перед отображением выполняется преобразование полученной матрицы в 8-битную целочисленную посредством вызова функции convertScaleAbs.
#include <stdio.h>
#include <opencv2/opencv.hpp>
using namespace cv;
const char helper[] =
"Sample_Laplacian.exe <img_file>\n\ \t<img_file> - image file name\n";
int main(int argc, char* argv[])
{
const char *initialWinName = "Initial Image",
*laplacianWinName = "Laplacian";
Mat img, grayImg, laplacianImg, laplacianImgAbs;
int ddepth = CV_16S;
if (argc < 2)
{
printf("%s", helper);
return 1;
}
// загрузка изображения
img = imread(argv[1], 1);
// сглаживание с помощью фильтра Гаусса
GaussianBlur(img, img, Size(3,3),
0, 0, BORDER_DEFAULT);
// преобразование в оттенки серого
cvtColor(img, grayImg, CV_RGB2GRAY);
// применение оператора Лапласа
Laplacian(grayImg, laplacianImg, ddepth);
convertScaleAbs(laplacianImg, laplacianImgAbs);
// отображение результата
namedWindow(initialWinName, CV_WINDOW_AUTOSIZE);
namedWindow(laplacianWinName, CV_WINDOW_AUTOSIZE);
imshow(initialWinName, img);
imshow(laplacianWinName, laplacianImgAbs);
waitKey();
// закрытие окон
destroyAllWindows();
// осовобождение памяти
img.release();
grayImg.release();
laplacianImg.release();
laplacianImgAbs.release();
return 0;
}
Далее показан результат выделения ребер с использованием оператора Лапласа (рис.9.8) на тестовом изображении, показанном ранее (рис.9.2, слева).



 "
"