Самостоятельная работа 2: Оптимизация вычислительно трудоемкого программного модуля для архитектуры Intel Xeon Phi. Линейные сортировки
Параллельная реализация
Простое слияние
Можно выделить два подхода к реализации параллельного алгоритма сортировки: внутренняя реализация параллельного алгоритма или внешнее распараллеливание за счёт слияния отсортированных частей.
Алгоритм побайтовой восходящей сортировки заключается в последовательном применении сортировки подсчётом к каждому байту чисел, поэтому параллельно может выполняться только сортировка подсчётом для каждого байта. При этом параллельная версия сортировки подсчётом должна сохраняться свойство устойчивости сортировки (а это тяжелая задача). Этот алгоритм будет рассмотрен позднее.
Идея параллельной реализации с использованием слияния заключается в выполнении следующих шагов:
- Сортировка частей массива.
- Слияние отсортированных частей массива.
Сортировка частей массива может выполняться без каких-либо синхронизаций, поэтому теоретическое ускорение этого этапа является линейным. Этап слияние в зависимости от алгоритма может иметь различную эффективность.
Идея простого слияния заключается в том, что один поток может выполнять слияние двух отсортированных массивов по классическому алгоритму. В этом случае слияние n массивов могут выполнять n/2 параллельных потоков. На следующем шаге слияние n/2 полученных массивов будут выполнять n/4 потоков и т.д. ( рис. 4.1). Таким образом, последнее слияние будет выполнять один поток, а учитывая, что сортировка частей массива имеет линейную трудоемкость, то слияние вносит существенный вклад во время работы алгоритма.
Создайте пустой файл main.cpp и скопируйте в него код из файла main_lsd1.cpp.
Параллельную реализацию слияния построим на основе рекурсивного алгоритма с использованием tbb::task. Каждый экземпляр класса LSDParallelSorter будет выполнять сортировку части массива либо за счёт вызова последовательного алгоритма (если размер сортируемой части массива достаточно мал), либо за счёт слияния уже отсортированных массивов с помощью метода Split().
class LSDParallelSorter:public task
{
private:
double *mas;
double *tmp;
int size;
int portion;
void Split(int size1, int size2)
{
for(int i=0; i<size1; i++)
tmp[i] = mas[i];
double *mas2 = mas + size1;
int a = 0;
int b = 0;
int i = 0;
while( (a != size1) && (b != size2))
{
if(tmp[a] <= mas2[b])
{
mas[i] = tmp[a];
a++;
}
else
{
mas[i] = mas2[b];
b++;
}
i++;
}
if (a == size1)
for(int j=b; j<size2; j++)
mas[size1+j] = mas2[j];
else
for(int j=a; j<size1; j++)
mas[size2+j] = tmp[j];
}
public:
LSDParallelSorter(double *_mas, double *_tmp, int _size,
int _portion): mas(_mas), tmp(_tmp),
size(_size), portion(_portion)
{}
task* execute()
{
if(size <= portion)
{
LSDSortDouble(mas, tmp, size);
}
else
{
LSDParallelSorter &sorter1 = *new (allocate_child())
LSDParallelSorter(mas, tmp, size/2, portion);
LSDParallelSorter &sorter2 = *new (allocate_child())
LSDParallelSorter(mas + size/2, tmp + size/2,
size - size/2, portion);
set_ref_count(3);
spawn(sorter1);
spawn_and_wait_for_all(sorter2);
Split(size/2, size - size/2);
}
return NULL;
}
};
Функция LSDParallelSortDouble() создаёт корневой task, начиная с которого будет разворачиваться рекурсия. В этой функции также создаётся вспомогательный массив размера size и выполняется вычисление размера порции, которая определяет, будет вызываться последовательный алгоритм поразрядной сортировки или, начиная с этого размера, будет выполняться слияние.
void LSDParallelSortDouble(double *inp, int size,
int nThreads)
{
double *out=new double[size];
int portion = size/nThreads;
if(size%nThreads != 0)
portion++;
LSDParallelSorter& sorter = *new (task::allocate_root())
LSDParallelSorter(inp ,out, size, portion);
task::spawn_root_and_wait(sorter);
delete[] out;
}
Далее осталось лишь заменить вызов функции сортировки.
... start = tick_count::now(); LSDParallelSortDouble(mas, size, nThreads); finish = tick_count::now(); ...
Соберите получившуюся реализацию для Intel Xeon Phi и проведите тест для 10 миллионов элементов при разном числе потоков на сопроцессоре. Результаты, полученные авторами на тестовой инфраструктуре, представлены на рис. 4.2.
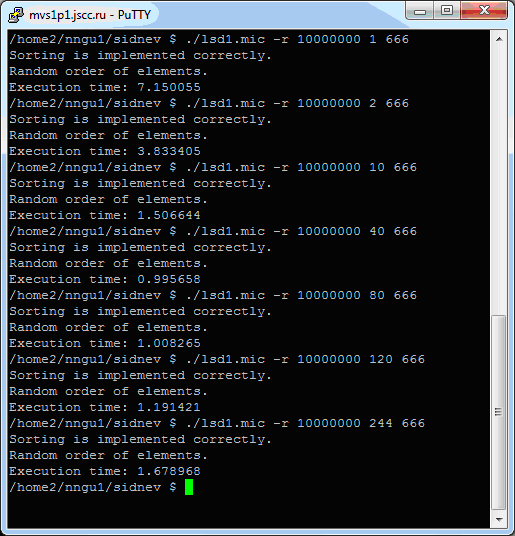
Рис. 4.2. Результаты работы параллельной побайтовой восходящей сортировки при использовании простого слияния на Intel Xeon Phi
Здесь мы запускали только вариант со случайным заполнением, но с разным числом потоков. Можно заметить, что время работы программы в 40 и 80 потоков практически не отличается. Это свидетельствует о том, что трудоёмкость побайтовой сортировки соизмерима со временем слияния массивов. При увеличении количества потоков количество слияний также увеличивается, а для небольшого массива элементов это приводит к тому, что слияние начинает занимать больше времени, чем сортировка. Из-за этого время работы программы в 120 и 244 потока ощутимо больше, чем в 40. Для наглядности приведём график времени сортировки 10 миллионов элементов с помощью параллельного алгоритма LSD с использованием простого слияния на сопроцессоре ( рис. 4.3).
увеличить изображение
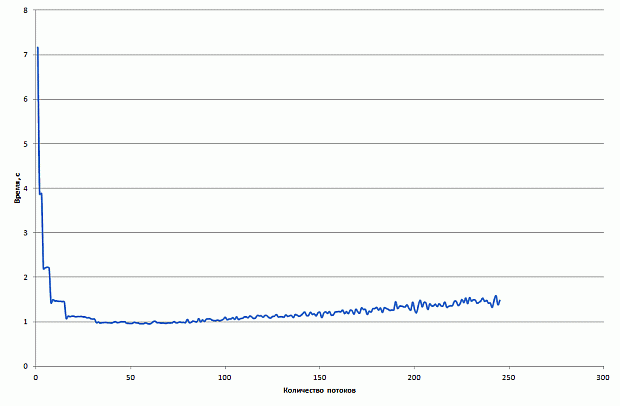
Рис. 4.3. Время сортировки 10 миллионов элементов с помощью параллельного алгоритма LSD с использованием простого слияния на Intel Xeon Phi
Ступенчатость графика вызвана особенностью параллельного алгоритма, который использует для вычислений только количество потоков равное степени 2. Остальные потоки просто не используются. Т.е. при запуске в  , потоков будет использоваться только из них. Приведём аналогичный график для 100 миллионов элементов.
, потоков будет использоваться только из них. Приведём аналогичный график для 100 миллионов элементов.
увеличить изображение
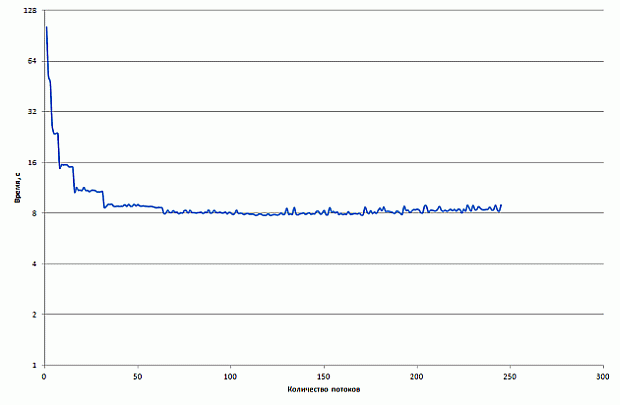
Рис. 4.4. Время сортировки 100 миллионов элементов с помощью параллельного алгоритма LSD с использованием простого слияния на Intel Xeon Phi
Максимальное ускорение, равное 13, достигается при использовании 128 потоков.