Самостоятельная работа 2: Оптимизация вычислительно трудоемкого программного модуля для архитектуры Intel Xeon Phi. Линейные сортировки
Введение
Хаос – это порядок, который нам непонятен.
Презентацию к лабораторной работе Вы можете скачать здесь.
Сортировка (упорядочивание) данных имеет очевидное практическое применение во многих областях (решение систем линейных уравнений, упорядочивание графов [ [ 4.3 ] ], базы данных и др.). На протяжении многих лет изучение алгоритмов сортировки является неотъемлемой частью курсов "Алгоритмы и структуры данных", читаемых как в российских, так и в зарубежных университетах. По данной теме по-прежнему публикуются статьи, предлагающие миру новые идеи и подходы к их реализации. Кажущаяся элементарность постановки задачи не должна удивлять математиков: не все, что просто формулируется, просто решается; чего только стоит известная проблема о доказательстве теоремы Ферма, решение которой потребовало столько времени и усилий. Казалось бы, причем тут сортировка? С проникновением информатики в школьную программу чуть ли не любой ученик выпускного класса может описать алгоритм для упорядочивания массива. Проблема, однако, в том, что таким, скорее всего весьма простым алгоритмом, не удастся воспользоваться при решении прикладных задач большой размерности, где объемы упорядочиваемых данных исчисляются десятками миллионов элементов. В современном мире число таких задач и их важность неуклонно растут. Решение их на одном компьютере становится невозможным, в дело вступают мощные вычислительные системы – кластеры и суперкомпьютеры, содержащие тысячи и десятки тысяч многопроцессорных многоядерных вычислительных устройств. Эффективное использование таких систем для упорядочивания данных является актуальной задачей.
Алгоритмы сортировки рассматриваются в огромном числе источников. Прежде всего, необходимо отметить фундаментальную работу [ [ 4.4 ] ], освещающую многие классические алгоритмы и раскрывающую методику их анализа. Полезно ознакомиться и с другими источниками, среди которых один из лучших в мире учебников по алгоритмам и структурам данных, подготовленный в MIT, первые два издания которого переведены на русский язык [ [ 4.2 ] ], а недавно вышедшее третье издание [ [ 4.1 ] ] содержит важные рекомендации по распараллеливанию сортировки слиянием. Также необходимо отметить работу М.В. Якобовского [ [ 4.3 ] ], рассмотревшего распараллеливание алгоритмов сортировки для кластерных систем. Есть и другие источники, безусловно заслуживающие внимания, среди которых как печатные издания [ [ 4.5 ] - [ 4.7 ] и др.], так и публикации в интернет [ [ 4.8 ] - [ 4.10 ] ].
Алгоритмы сортировки можно классифицировать по-разному. Для одних алгоритмов время работы существенно зависит от входных данных, для других – нет. Одни алгоритмы быстро сортируют уже упорядоченные или почти упорядоченные массивы, другие не обладают таким свойством. Некоторые сортировки упорядочивают данные без использования дополнительной памяти (in-place), другие требуют создания дополнительных массивов. Обратим основное внимание на время работы. С этой точки зрения можно разделить множество алгоритмов сортировки на те, которые основаны на использовании операции сравнения (время работы  , и, те, которые, как это не странно звучит, обходятся без нее (время работы
, и, те, которые, как это не странно звучит, обходятся без нее (время работы 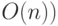 . Имеющаяся литература наиболее подробно описывает первый класс алгоритмов, выделяя в нем медленные "пузырьковые" сортировки, работающие за время
. Имеющаяся литература наиболее подробно описывает первый класс алгоритмов, выделяя в нем медленные "пузырьковые" сортировки, работающие за время  (метод выбора, метод вставки, метод пузырька и др.), и так называемые "быстрые" сортировки (сортировка слиянием, метод Хоара, сортировка кучей и др.), в среднем работающие за время
(метод выбора, метод вставки, метод пузырька и др.), и так называемые "быстрые" сортировки (сортировка слиянием, метод Хоара, сортировка кучей и др.), в среднем работающие за время 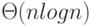 . Теоретически доказано, что этот результат является наилучшим в данном классе. По нашим наблюдениям и публикациям в открытой печати наибольшей популярностью на практике пользуется сортировка Хоара, не требующая дополнительной памяти, имеющая малую константу при
. Теоретически доказано, что этот результат является наилучшим в данном классе. По нашим наблюдениям и публикациям в открытой печати наибольшей популярностью на практике пользуется сортировка Хоара, не требующая дополнительной памяти, имеющая малую константу при 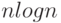 nlogn и простая в реализации. Главный недостаток алгоритма, состоит в том, что время его работы в худшем случае все-таки достигает
nlogn и простая в реализации. Главный недостаток алгоритма, состоит в том, что время его работы в худшем случае все-таки достигает 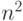 , однако при случайном выборе ведущего элемента (pivot) этого почти никогда не происходит. Алгоритм может быть реализован как рекурсивно, так и итеративно. Итеративная реализация с использованием собственного стека более безопасна с точки зрения отсутствия проблемы переполнения системного стека, а также ориентировочно на 20% быстрее рекурсивной (в книге [
[
4.7
]
] приведены рекомендации по подготовке итеративной версии). Еще одно важное достоинство метода Хоара состоит в достаточно эффективном использовании кэш-памяти.
, однако при случайном выборе ведущего элемента (pivot) этого почти никогда не происходит. Алгоритм может быть реализован как рекурсивно, так и итеративно. Итеративная реализация с использованием собственного стека более безопасна с точки зрения отсутствия проблемы переполнения системного стека, а также ориентировочно на 20% быстрее рекурсивной (в книге [
[
4.7
]
] приведены рекомендации по подготовке итеративной версии). Еще одно важное достоинство метода Хоара состоит в достаточно эффективном использовании кэш-памяти.
В данной лабораторной работе рассматривается алгоритм из другого класса, работающий за время  .
.  , – линейная поразрядная сортировка (Radix Sort). Практика показывает, что указанный алгоритм не слишком сложен в программной реализации и хорошо себя показывает при упорядочивании огромных объемов данных. Одна из главных проблем – распараллеливание. Зачастую получается, что лучший последовательный алгоритм имеет сугубо последовательную природу, в связи с чем приходится либо брать менее эффективный, но распараллеливаемый алгоритм, либо делить массив на блоки с целью их сортировки и последующего слияния. Демонстрации подобных проблем и некоторых подходов к их решению в существенно многоядерных системах с общей памятью посвящена данная лабораторная работа.
, – линейная поразрядная сортировка (Radix Sort). Практика показывает, что указанный алгоритм не слишком сложен в программной реализации и хорошо себя показывает при упорядочивании огромных объемов данных. Одна из главных проблем – распараллеливание. Зачастую получается, что лучший последовательный алгоритм имеет сугубо последовательную природу, в связи с чем приходится либо брать менее эффективный, но распараллеливаемый алгоритм, либо делить массив на блоки с целью их сортировки и последующего слияния. Демонстрации подобных проблем и некоторых подходов к их решению в существенно многоядерных системах с общей памятью посвящена данная лабораторная работа.
Ускорители являются специализированными вычислителями и не предназначены для эффективного решения всех существующих задач. Они часто используются при решении задач, в которых допускается эффективная векторная обработка данных и имеется большой запас внутреннего параллелизма. В данной работе специально рассматривается "тяжелая" задача для реализации на сопроцессоре, в которой огромное число операций доступа к памяти и практически нет вычислений. В работе демонстрируются некоторые подходы к оптимизации и распараллеливанию подобных приложений.
Методические указания
Цели и задачи работы
Цель данной работы – изучение подходов к распараллеливанию алгоритмов упорядочивания данных, работающих за линейное время, в существенно многоядерных системах.
Данная цель предполагает решение следующих основных задач:
- Подготовка тестовой инфраструктуры для проведения экспериментов с последовательными и параллельными реализациями алгоритмов сортировки больших вещественных массивов данных.
- Рассмотрение разных способов распараллеливания алгоритма LSD для традиционных систем с общей памятью, а также существенно многоядерных систем на базе Intel Xeon Phi, анализ результатов, выявление существующих проблем и обсуждение возможных подходов к их решению.
- Демонстрация подходов к оптимизации и распараллеливанию программ, решающих задачи, изначально достаточно "тяжелые" для эффективной параллельной реализации.
Структура работы
Работа построена следующим образом. Ставится задача упорядочивания данных. Описываются подходы к распараллеливанию одного из самых эффективных алгоритмов линейной сортировки (LSD). Проводится сравнение с параллельной сортировкой, включенной в библиотеку Intel TBB. Изучаются проблемы при распараллеливании алгоритма LSD и возможные подходы к их решению. Результаты подтверждаются вычислительными экспериментами, как на процессорах общего назначения, так и на сопроцессоре Intel Xeon Phi. Студентам предлагаются задачи для самостоятельной проработки.
Тестовая инфраструктура
Вычислительные эксперименты проводились с использованием инфраструктуры представленной в таблице ниже (табл.4.1).
| Процессор | 2 восьмиядерных процессора Intel Xeon E5-2690 (2.9 GHz) |
| Память | 64 GB |
| Операционная система | Linux CentOS 6.2 |
| Сопроцессор | 2 сопроцессора Intel Xeon Phi 7110X (61 ядро) |
| Компилятор, профилировщик, отладчик, математическая библиотека | Intel Parallel Studio XE 2013:
|
Рекомендации по проведению занятий
Для выполнения лабораторной работы рекомендуется следующая последовательность действий.
- Дать введение в проблематику упорядочивания больших объемов данных, обзор наиболее показательных алгоритмов.
- Описать программную инфраструктуру для проведения экспериментов.
- Провести вычислительные эксперименты с последовательной реализацией алгоритма LSD. Убедиться в корректности, обратить внимание на производительность.
- Реализовать параллельные алгоритмы для систем с общей памятью с применением разных подходов. Рассмотреть подходы к разработке параллельных программ под Intel Xeon Phi и обсудить результаты экспериментов. Выполнить анализ полученных результатов.
- Сформулировать основные выводы, дать задания для самостоятельной проработки
Разработка проекта
Возьмём за основу последовательную версию сортировки LSD из лабораторной работы "Сортировки" из курса "Параллельные численные методы". Заметим, что в указанной работе разработка выполнялась под ОС Windows, в то время как в текущей – будет выполняться под ОС Linux (CentOS 6.2). Это отличие является существенным и мы его будем учитывать при разработке.
В процессе разработки будут использовать следующие инструменты:
- PuTTY – доступ к консоли Linux [ [ 4.16 ] ];
- WinSCP – манипуляция с файлами [ [ 4.17 ] ];
- mcedit, vi – текстовые редакторы [ [ 4.18 ] ];
- icc – компилятор Intel C++ Compiler;
- taskset – выбор ядер, на которых будет запускаться приложение.
Портировние под Linux
Разработанный программный код LSD не получится сразу скомпилировать под Linux:
- В Linux нет заговочного файла windows.h. Строку #include "windows.h" необходимо удалить из программного кода.
- Измерение времени с помощью функций QueryPerformanceCounter не поддерживается в Linux.
Внесём изменения в программный код. Время будем измерять с помощью функций TBB. Добавим требуемый заголовочный файл:
#include "tbb/tick_count.h"
Внесём изменения в программный код измерения времени функции main:
tick_count start, finish;
…
start = tick_count::now();
LSDSortDouble(mas, size, nThreads);
finish = tick_count::now();
…
printf("Execution time: %lf\n",
(finish - start).seconds());
Сборка программы под Linux
Скопируйте исходные коды портированной версии поразрядной сортировки LSD (main.cpp) на машину под управлением Linux с помощью WinSCP. Зайдите на машину с установленным Intel C++ Compiler с помощью PuTTY и выполните сборку программы:
-sh-4.1$ icc -tbb -mkl -lrt main.cpp -o sort.out
В результате будет собран исполняемый модуль sort.out1Если переменные окружения не настроены, то можно указать полный путь к библиотекам для линковки, например: icc -mkl -lrt main.cpp /opt/software/intel/composer_xe_2013.1.117/tbb/lib/intel64/libtbb.so.2 -o sort.out .
Сборка под Intel Xeon Phi
Для сборки программы под Intel Xeon Phi нужно добавить ключ –mmic:
-sh-4.1$ icc –mmic -tbb -mkl -lrt main.cpp -o sort_mic.out
Полученная после компиляция программа sort_mic.out должна запускаться непосредственно на сопроцессоре Intel Xeon Phi.
Проведение экспериментов
Для проведения экспериментов удобно использовать скрипты. Ниже приведён пример скрипта на Shell для проведения серийных экспериментов. Для удобства дальнейшей обработки, формат вывода программы sort.out был изменён:
#!/bin/sh
var0_end=245
var1=5000000
var1_end=105000000
step=5000000
while test "$var1" != "$var1_end"
do
var0=1
while test "$var0" != "$var0_end"
do
./sort.out -r $var1 $var0 666 >> log_$var1
./sort.out -r $var1 $var0 666 >> log_$var1
./sort.out -r $var1 $var0 666 >> log_$var1
echo "" >> log_$var1
echo "$var1 $var0 "
var0=`expr $var0 + 1`
done
var1=`expr $var1 + $step`
done
С помощью подобных скриптов проводились эксперименты как на хостовой машине с процессором общего назначения, так и на сопроцессоре Intel Xeon Phi.
Обратим особое внимание на архитектуру процессоров, на которых будут проводиться эксперименты (табл. 1). На хостовой машине установлено два процессора Intel Xeon E5-2690 с базовой частотой 2.9 GHz. Каждый процессор содержит 8 ядер по 2 потока на каждом (Hyper Threading). Таким образом, на хостовой машине доступно 32 логических процессора. Нумерация ядер в системе следующая2На основании содержимого файла /proc/cpuinfo.:
- логические процессоры с номером от 0 до 7 – ядра первого процессора (первые потоки),
- от 8 до 15 – ядра первого процессора (вторые потоки),
- от 16 до 23 – ядра второго процессора (первые потоки),
- от 24 до 31 – ядра второго процессора (вторые потоки).
Итак, каждая пара логических процессоров с номерами (0, 8), (1, 9), (2, 10) и т.д. принадлежат отдельному ядру. Таким образом, параллельную программу в 2 потока можно запустить тремя различными способами, которые будут отличаться использованием аппаратных возможностей системы:
- На одном ядре (например, на логических ядрах 0 и 8).
- На двух ядрах одного процессора (например, на логических ядрах 0 и 1).
- На двух ядрах разных процессоров (например, на логических ядрах 0 и 16).
С помощью утилиты taskset можно задать ядра, на которых будет запускаться приложение. Таким образом, планировщик потоков ОС будет распределять потоки программы только между этими ядрами. Обратим внимание, что привязки потоков к ядрам происходить не будет – потоки могут перемещаться между ядрами. Для запуска приложения не более чем по одному потоку на ядро можно использовать утилиту taskset следующим образом:
-sh-4.1$ taskset -c 0-7,16-23 ./sort.out –r 1000000 16 666
Сопроцессор Intel Xeon Phi 7110X имеет 61 ядро по 4 потока на каждом (244 логических процессора). Базовая частота ядер 1.2 Ghz. Нумерация ядер отличается от хостовой. Логические процессоры в группах с номерами (1, 2, 3, 4), (5, 6, 7, 8) и т.д. принадлежат отдельному ядру. Стоить обратить внимание на логический процессор с номером ноль. Он принадлежит одному ядру вместе с логическими процессорами 241, 242, 243.
