Лекция 2: Принципы переноса прикладных программных пакетов на Intel Xeon Phi
Введение
Презентацию к лекции Вы можете скачать здесь.
В 2012 году корпорация Intel представила на рынке новый сопроцессор – Intel Xeon Phi, построенный в рамках парадигмы manycore и содержащий 61 вычислительное ядро близкой к x86 архитектуры. В отличие от других активно применяющихся представителей manycore-архитектур, в частности, GPU, Intel сделала акцент не только на пиковой производительности устройства, но и на существенном упрощении процесса создания новых и портирования существующих программных пакетов путем использования стандартных языков и технологий для параллельного программирования.
Так, в ряде случаев можно обойтись без какой-либо переработки существующего кода, добавив ключ компилятора и получив программу, способную выполняться на Xeon Phi. Производительность результата подобного портирования на Xeon Phi зависит от многих факторов и может варьироваться от многократного замедления до многократного ускорения по сравнению с исходной версией на CPU.
Существенное замедление может наблюдаться для приложений, значительная часть (по вкладу в общее время) которых выполняется последовательно, либо задач, не имеющих достаточный ресурс параллелизма для использования большого количества ядер Xeon Phi. Напротив, приложения с большой долей и степенью параллелизма, написанные с учетом векторизации, могут достигать высокой производительности на Xeon Phi без дополнительных усилий. На практике же обычно имеет место некий средний случай – в результате начального портирования приложение на Xeon Phi демонстрирует производительность, сравнимую с версией на CPU, но далекую от пиковой производительности Xeon Phi; таким образом, огромные вычислительные ресурсы Xeon Phi используются далеко не полностью.
В этом случае возникает вопрос, какие усилия требуются для того, чтобы превратить программу, работающую на CPU, в программу, эффективно работающую на Xeon Phi? Этот и другие подобные вопросы, определенно, представляют интерес для научного сообщества. В литературе появляются первые работы, рассказывающие об опыте портирования на Xeon Phi приложений из разных областей.
Анализ позволяет сделать следующий вывод: портирование программ на Xeon Phi может быть выполнено в весьма сжатые сроки (несколько дней) даже при весьма значительных объемах кода. При этом код будет работать достаточно эффективно только в тех случаях, когда приложение уже было оптимизировано для CPU и содержало большой запас внутреннего параллелизма как с точки зрения многопоточности, так и с точки зрения использования инструкций SIMD. Данное условие является необходимым, но не достаточным. Так, многие алгоритмы успешно распараллеливаются на 8 16, но не на 120 240 потоков, допускают эффективное использование SIMD для небольшой длины регистра, упираются в ограниченный на Xeon Phi объем встроенной памяти, требуют вдумчивой реализации с целью активного использования команд Fused Multiply-Add (FMA) и т.д. Все это означает, что получение максимальной производительности требует от программиста определенных усилий.
В данной лекции рассматриваются подходы к портированию и оптимизации на Xeon Phi двух прикладных программных пакетов, осуществляющих решение задач вычислительной физики: моделирование динамики электромагнитного поля методом FDTD (раздел 2) и моделирование переноса излучения методом Монте-Карло (раздел 3). Используются типичные приемы оптимизации, способные привести к выигрышу производительности в рамках multicore- и manycore-архитектур.
Подходы к оптимизации программного пакета для моделирования динамики электромагнитного поля методом FDTD
Одним из широко используемых методов вычислительной электродинамики является метод FDTD (Finite-Difference Time-Domain) [2.1]. Это явный конечно-разностный метод численного решения уравнений Максвелла. Особенностью метода является использование специальной сетки для компонент электромагнитного поля. Точки пространства, соответствующие разным компонентам поля, сдвинуты относительно друг друга на половинные шаги по пространству и времени, благодаря чему все конечно-разностные аппроксимации первых производных являются центральными, и достигается второй порядок точности по времени и пространственным компонентам.
В данном разделе рассматривается портирование на Xeon Phi и оптимизация реализации метода FDTD, созданной на основе программного пакета для моделирования плазмы PICADOR [2.2]. Для простоты рассматривается базовая версия FDTD. На практике вместе с FDTD часто используется приграничный поглощающий слой PML, оптимизация с его учетом рассматривается в [2.3].
Общее описание метода FDTD
Рассматривается трехмерная область в виде прямоугольного параллелепипеда
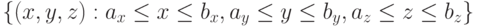 ,
которую в дальнейшем будем называть расчетной областью. В каждый момент времени
,
которую в дальнейшем будем называть расчетной областью. В каждый момент времени  в каждой точке расчетной области
в каждой точке расчетной области 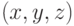 определены 3-компонентное электрическое поле, которое будем обозначать
определены 3-компонентное электрическое поле, которое будем обозначать 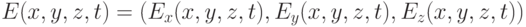 , и 3-компонентное магнитное поле
, и 3-компонентное магнитное поле 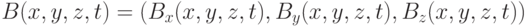 . Пара векторных полей
. Пара векторных полей 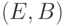 называется электромагнитным полем.
называется электромагнитным полем.
Рассматривается задача моделирования динамики электромагнитного поля от начального момента времени 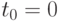 до заданного конечного момента времени
до заданного конечного момента времени 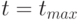 . Динамика электромагнитного поля подчиняется системе уравнений Максвелла (приведена запись двух уравнений для случая вакуума в системе единиц СГС,
. Динамика электромагнитного поля подчиняется системе уравнений Максвелла (приведена запись двух уравнений для случая вакуума в системе единиц СГС,  – скорость света в вакууме):
– скорость света в вакууме):
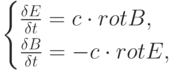
Для численного решения задачи расчетная область покрывается равномерной пространственной сеткой, содержащей 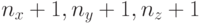 узлов (
узлов (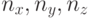 ячеек) по соответствующим размерностям. Шаги сетки равны
ячеек) по соответствующим размерностям. Шаги сетки равны  . Моделирование по времени происходит с заданным шагом
. Моделирование по времени происходит с заданным шагом  , т.е. в дискретные моменты 0,
, т.е. в дискретные моменты 0, 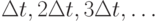 , последовательность завершается при превышении
, последовательность завершается при превышении 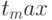 . Для индексирования узлов сетки используются естественные трехмерные индексы
. Для индексирования узлов сетки используются естественные трехмерные индексы 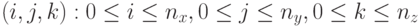 .
.
FDTD использует специальную сетку (сетку Yee [2.1]) следующего вида. Сеточное значение  соответствует точке физического пространства
соответствует точке физического пространства
 соответствует точке
соответствует точке 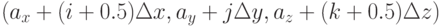 и
и 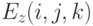 – точке
– точке  . Сеточные значения компонент магнитного поля
. Сеточные значения компонент магнитного поля 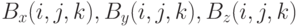 сооветствуют точкам
сооветствуют точкам 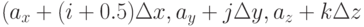 ,
, 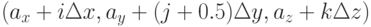 ,
, 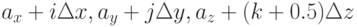 . Таким образом, разные компоненты поля сдвинуты относительно центра соответствующей ячейки на полшага по одной или двум осям. Кроме того, компоненты магнитного поля сдвинуты относительно компонент электрического поля на полшага вперед по времени.
. Таким образом, разные компоненты поля сдвинуты относительно центра соответствующей ячейки на полшага по одной или двум осям. Кроме того, компоненты магнитного поля сдвинуты относительно компонент электрического поля на полшага вперед по времени.
Моделирование производится итерационно по времени, на каждом шаге хранится текущий набор сеточных значений поля. Начальные значения поля определяются из заданных начальных условий. Итерация метода состоит из двух этапов: использование текущих значений  и
и  для вычисления новых значений
для вычисления новых значений  (обновление
(обновление  ), использование текущих значений
), использование текущих значений  и новых значений
и новых значений  для вычисления новых значений
для вычисления новых значений  (обновление
(обновление  ). В приводимых далее формулах подразумевается, что вычисления производятся для всех узлов сетки
). В приводимых далее формулах подразумевается, что вычисления производятся для всех узлов сетки 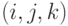 , для которых все члены правой части определены. Обновление
, для которых все члены правой части определены. Обновление  выполняется по следующей схеме:
выполняется по следующей схеме:
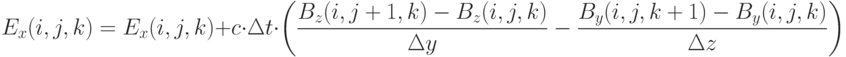
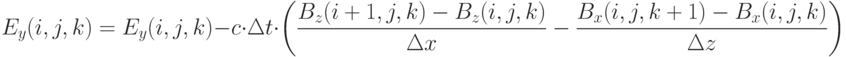
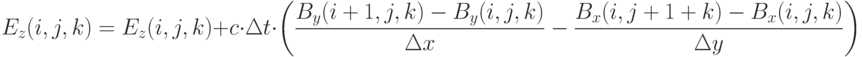
Обновление  выполняется по следующей схеме:
выполняется по следующей схеме:
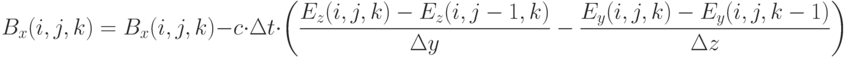
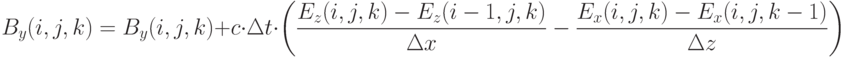
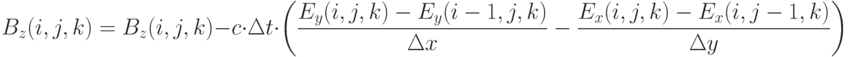
Очевидно, данные формулы не могут быть использованы для обновления значений  на "правой" границе сетки (
на "правой" границе сетки (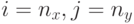 или
или  ), и для обновления значений
), и для обновления значений  на "левой" границе (
на "левой" границе (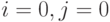 или
или 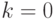 ). Способ вычисления данных сеточных значений зависит от используемых граничных условий. В данном разделе используются периодические граничные условия по всем осям:
). Способ вычисления данных сеточных значений зависит от используемых граничных условий. В данном разделе используются периодические граничные условия по всем осям: 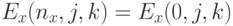 ,
, , аналогично для других границ и компонент поля.
, аналогично для других границ и компонент поля.
