|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Лекция 18: Выбор решений при неизвестных состояниях природы (игры с природой)
Вероятностные модели прогнозирования и оценки состояний природы (модели с испытаниями)}
Рассмотренная выше задача является примером операции с единственной
оперирующей стороной. В связи с этим, выбор решения не осложняется
конфликтом интересов. Основная трудность выбора в таких условиях связана
с влиянием на исход операции неизвестного состояния природы  , что интерпретируется как наличие неопределенности.
В связи с этим, в таких операциях обычно оцениваются не выигрыши оперирующей стороны, а ее потери
, что интерпретируется как наличие неопределенности.
В связи с этим, в таких операциях обычно оцениваются не выигрыши оперирующей стороны, а ее потери  ,
вызываемые принятием решения a в ситуации, когда природа находится
в состоянии
,
вызываемые принятием решения a в ситуации, когда природа находится
в состоянии  . Подобные задачи
часто интерпретируются как антагонистические игры с природой, в которых
единственная реально имеющая интересы оперирующая сторона (называемая статистиком ) рассматривается как второй
игрок (см. замечание 1.3 в
"Математическая модель задачи выбора решений"
).
. Подобные задачи
часто интерпретируются как антагонистические игры с природой, в которых
единственная реально имеющая интересы оперирующая сторона (называемая статистиком ) рассматривается как второй
игрок (см. замечание 1.3 в
"Математическая модель задачи выбора решений"
).
В дальнейшем мы ограничимся случаем, когда множество возможных состояний
природы  и множество возможных решений
статистика A являются конечными, т.е.
и множество возможных решений
статистика A являются конечными, т.е.
 |
( 17.5) |
 могут быть
охарактеризованы вероятностями их наступления
могут быть
охарактеризованы вероятностями их наступления  ,
,  . Это важное
допущение позволяет накапливать информацию о состояниях природы с помощью наблюдений, на основании которых оцениваются распределения
. Это важное
допущение позволяет накапливать информацию о состояниях природы с помощью наблюдений, на основании которых оцениваются распределения |
( 17.6) |
Помимо распределений (17.6), позволяющих прогнозировать неизвестное состояние природы на основании результатов (длительных) наблюдений, оценка текущего состояния может осуществляться с помощью экспериментов.
Пример 4.2 (диагностика туберкулеза) Органы здравоохранения проводят обследование
населения некоторой территории с целью выявления и последующего лечения
больных туберкулезом2Туберкулез относится к числу старейших
известных заболеваний. В четырех египетских мумиях (относимых к XXVII веку
до новой эры) обнаружены туберкулезные повреждения позвоночника. В начале
XX века (только в Европе) туберкулез был причиной смерти около одного
миллиона человек (ежегодно). Микробактерия туберкулеза (палочка Коха)
открыта в 1882 году. Заболевание по наследству не передается.. В отношении
каждого обследуемого принимается решение, следует ли ему пройти курс
лечения (a=2) или он не нуждается в таком лечении (a=1)? Это
очевидным образом предполагает два состояния, в которых может находиться пациент3Выбор нумерации решений (a) и состояний природы  определяется соображениями, которые будут рассмотрены позднее.
"здоров"
определяется соображениями, которые будут рассмотрены позднее.
"здоров"  и "болен"
и "болен" 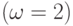 .
.
Одной из типичных форм обследования, широко применяемых для раннего выявления туберкулеза (например, у детей), является использование пробы Манту4Реакция Манту - аллергическая диагностическая проба с внутрикожным введением туберкулина. Вздутие кожи (инфильтрат), наблюдаемое через 72 часа и имеющее размер более 5 мм, считается положительной реакцией. Предложена французским ученым Шарлем Манту в 1908 году. (для лиц старше 12 лет обычно используется флюорография). Эксперименты такого рода, целью которых является установление состояния природы, мы будем называть испытаниями. Каждой схеме испытаний можно сопоставить множество Z возможных исходов z, которое мы будем полагать конечным, т.е.
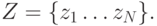 |
( 17.7) |
Заметим, что, в случае пробы Манту, каждый исход представляет собой (измеренную с помощью линейки) ширину инфильтрата. При этом, хотя и нет однозначной связи между шириной инфильтрата и наличием заболевания, тем не менее существует достаточно выраженная статистическая связь, которая может быть охарактеризована следующим образом.
Введем функции p1(z) и p2(z), соответствующие
вероятностям появления
инфильтрата с показателем  у лиц, не имеющих заболевания
(функция p1 ), и у лиц, имеющих заболевание (функция p2 ). Эти
функции определяются свойствами пробы Манту и могут быть установлены на
основании анализа статистики испытаний для пациентов с заранее известным
диагнозом. Допустим, что графики этих функций подобны кривым,
представленным на рис. 4.2.
В таком случае бoльшая ширина инфильтрата
действительно типична для лиц, пораженных заболеванием. Этим определяется
практическая применимость пробы Манту, хотя не исключаются и ошибки из-за
острой аллергической реакции у некоторых здоровых людей или вялой реакции
у некоторых больных.
у лиц, не имеющих заболевания
(функция p1 ), и у лиц, имеющих заболевание (функция p2 ). Эти
функции определяются свойствами пробы Манту и могут быть установлены на
основании анализа статистики испытаний для пациентов с заранее известным
диагнозом. Допустим, что графики этих функций подобны кривым,
представленным на рис. 4.2.
В таком случае бoльшая ширина инфильтрата
действительно типична для лиц, пораженных заболеванием. Этим определяется
практическая применимость пробы Манту, хотя не исключаются и ошибки из-за
острой аллергической реакции у некоторых здоровых людей или вялой реакции
у некоторых больных.
Примем также, что на обследуемой территории длительное время ведется сбор статистики заболеваний. Наличие такой статистики позволяет интерпретировать долю населения, пораженную туберкулезом, как вероятность соответствующего состояния природы. Разумеется, что использование подобных оценок для целей прогнозирования имеет смысл лишь в случае, если указанные выборочные частоты стационарны (т.е. не имеют тенденции к быстрым изменениям)5Случай принятия решений в отсутствие такой статистики будет рассмотрен в "Проверка простой гипотезы относительно простой альтернативы" .
Согласно сделанным предположениям, вероятность того, что реакция Манту
даст результат  , описывается величиной
, описывается величиной
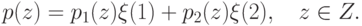
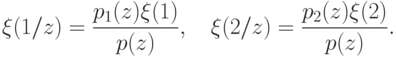
Таким образом, в общем случае, которому соответствуют множества (17.5), введение испытаний, характеризуемых исходами из (17.7) и распределениями
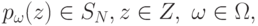 |
( 17.8) |
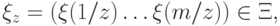 |
( 17.9) |
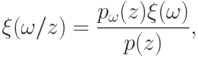 |
( 17.10) |
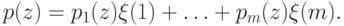 |
( 17.11) |
Замечание 4.1 (об однократном и многократном проведении испытаний). В рассмотренном примере результат (исход) каждого испытания представлял собой число. В общем случае он может быть и более сложным объектом (например, вектором или графическим образом). Однако в любом случае мы полагаем, что после реализации выборки (т.е. проведения испытания) результат z доступен "целиком" и не подлежит какому-либо уточнению. О таких испытаниях говорят, что они характеризуются фиксированным объемом выборки.
Альтернативный вариант состоит в том, что (в целях экономии средств)
эксперименты проводятся сначала на части образцов. Затем на основании
анализа полученных результатов принимается либо окончательное
решение 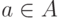 , либо решение о продолжении экспериментов на
оставшейся части образцов (таких стадий в осуществлении испытаний может
быть несколько). В этих случаях говорят об испытаниях с
последовательными выборками. Обсуждение их мы отложим до
заключительной части
"Проверка простой гипотезы относительно простой альтернативы"
.
, либо решение о продолжении экспериментов на
оставшейся части образцов (таких стадий в осуществлении испытаний может
быть несколько). В этих случаях говорят об испытаниях с
последовательными выборками. Обсуждение их мы отложим до
заключительной части
"Проверка простой гипотезы относительно простой альтернативы"
.

