|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Распределение информации и устойчивость решений
Продолжим обсуждение проблемы устойчивости решений. В следующем примере1Пример взят из работы: П.Р. Стронгин. Моделирование некоторых механизмов ценообразования// Дис. на соискание ученой степени кандидата физико-математических наук. М.: ВЦ РАН, 1997. рассматривается игра двух лиц, в роли которых выступают два разнотипных участника рынка - производитель и потребитель товара. Оказывается, отношения таких разнотипных участников не могут быть приведены в состояние, отвечающее рассмотренной выше концепции равновесия по Нэшу. Вместе с тем, эта модель позволяет обнаружить существование другого типа устойчивого поведения сторон, называемого равновесием по Штакельбергу. Источником этой новой формы устойчивости является (как и в случае равновесия по Нэшу ) стремление сторон к обеспечению своих интересов путем максимизации соответствующих критериев эффективности. Однако при этом учитываются последствия разнородности участников. Предполагается, что производитель P2 (выбирая стратегию y своего поведения) быстро приспосабливается к существующим условиям спроса (определяемым стратегией x потребителя P1 ). Как следствие, любая ситуация, возникающая в такой модели, может быть охарактеризована парой стратегий вида (x,y(x)). Взаимодействие сторон в таких моделях, характеризуемых несимметричным распределением информации, часто интерпретируют как отношения "лидера" и "ведомого"2Взаимодействия такого типа впервые рассматривались экономистом Г.Штакельбергом, изучавшим в начале ХХ века стратегии фирм, конкурирующих на одном и том же рынке. (роль которых в нашем случае играют, соответственно потребитель и производитель).
Пример 1.3 (отношения производителя и потребителя на рынке одного товара). Примем, что зависимость спроса D на (бесконечно дробимый) однородный товар от цены p за единицу этого товара описывается функцией вида
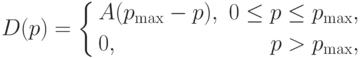 |
( 4.1) |
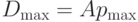 |
( 4.2) |
Примем также, что поступление товара на рынок характеризуется функцией предложения:
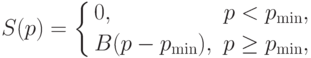 |
( 4.3) |
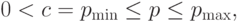 |
( 4.4) |
Замечание 1.13 (о функциях спроса и предложения ). 1. Понятия функций спроса и предложения являются достаточно старыми (см., например, книгу3Маршалл А. Принципы экономической науки. Т. I-III. М.: ПРОГРЕСС, УНИВЕРС. 1993. А.Маршалла4Маршалл Альфред (1842-1924) - английский экономист, основатель Кембриджской школы политэкономии. . Они широко используются для анализа различных рынков, таких, например, как рынки нефти, зерна, автомобилей и др. Эти понятия нашли применение и в анализе различных финансовых рынков. К их числу относятся рынки кредитов, капиталов, ценных бумаг, активов, страховок и др. При этом построение функций спроса и предложения для каждой конкретной задачи может потребовать достаточно сложных исследований.
2. В ряде актуальных задач, касающихся рынков одного товара со многими потребителями и производителями, можно использовать агрегированные функции спроса и предложения, сводя множество всех участников к единственному продавцу и единственному покупателю. Возможность такого агрегирования требует специального изучения в каждом конкретном случае. К числу первых примеров успешного анализа взаимодействий на рынке со многими участниками, основанного на сведении этих взаимодействий к отношениям двух сторон, относятся рынки с совершенной конкуренцией, характеризуемые следующими допущениями5См., например, работу: Петров А.А., Поспелов И.Г. , Шананин А.А. Опыт математического моделирования экономики. М.: Энергоатомиздат. 1996.:
- помимо того, что товар, выпускаемый разными производителями, считается однородным, все потребители считаются идентичными с точки зрения продавцов и для них (продавцов) нет никакого преимущества (или потери преимущества) при продаже товара тому или иному конкретному потребителю;
- производители и потребители считаются многочисленными, и продажа или покупка, осуществляемые любым из них, полагаются малыми по сравнению с общим объемом продаж на рынке;
- производители и потребители обладают полной информацией относительно цены, превалирующей в текущих торгах; при этом интересы производителей состоят в том, чтобы увеличить прибыль, а интересы потребителей характеризуются стремлением закупить возможно большее количество товара;
- выход на рынок и оставление его являются свободными и для производителей, и для потребителей.
Первое условие подразумевает анонимность производителей и потребителей. Товар одних производителей считается неотличимым от товара других (т.е. торговые марки и метки качества не используются), и, следовательно, потребители не имеют оснований предпочесть продукт одного производителя продукту другого. С другой стороны, благодаря однородности потребителей, производитель заинтересован продать товар тому из них, кто предложил большую цену. При этом другие критерии выбора покупателя, такие, например, как первоочередное обслуживание пришедших первыми, не рассматриваются.
3. Существуют реальные рынки, для которых справедлива принятая в (4.1)и (4.2) линейная зависимость соответственно спроса и предложения от цены p за единицу товара (при вариациях цены в пределах диапазона (4.4). К их числу относятся, например, некоторые рынки пшеницы6Пиндайк Р., Рубинфельд Д. Микроэкономика. М.: Экономика, Дело. 1992..
Однако в общем случае указанное допущение линейных функций спроса и предложения является некоторым упрощением реально наблюдаемых взаимосвязей. Применимость предположения о линейном характере обсуждаемых зависимостей существенно расширяется, если рассматриваются малые колебания цены относительно некоторого значения. Именно этот случай мы и будем рассматривать.
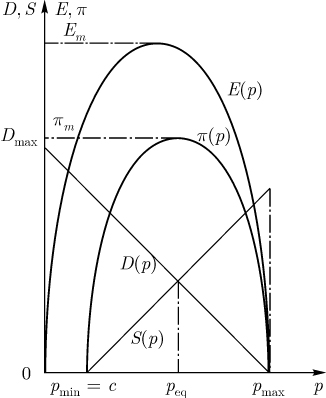
4. В экономической литературе при описании функций спроса и предложения цена p обычно откладывается по оси ординат, а ось абсцисс служит для задания количества товара. Для целей рассмотрения, проводимого ниже, удобнее связать цену с осью абсцисс (как это и сделано на рис.1.9). Такое использование координатных осей также встречается в литературе.
Продолжим рассмотрение модели. Цена peq, при которой существует баланс спроса и предложения и, следовательно, весь произведенный товар покупается, формально определяется как решение уравнения
 |
( 4.5) |
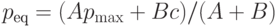 |
( 4.6) |
Квадратичная функция E(p), где
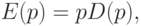
 |
( 4.7) |
 |
( 4.8) |
Из (4.2) и (4.7) следуют оценки
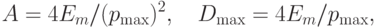 |
( 4.9) |
 |
( 4.10) |
Теперь введем квадратичную функцию
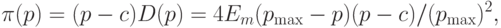 |
( 4.11) |
 и
и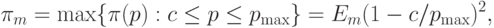 |
( 4.12) |
 |
( 4.13) |
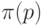 для случая, когда
для случая, когда  ).
).