|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Стратегическое равновесие в 2 x 2 играх
Случай единственного устойчивого решения, не реализуемого в чистых стратегиях
Первый и третий случаи, рассмотренные в заключительном пункте приведенного
выше доказательства теоремы, необходимо включают в число устойчивых
решений некоторую пару (x*,y*), образом которой является
одна из вершин квадрата D. Это означает, что в таком решении каждая из
сторон использует с единичной вероятностью одну из своих чистых
стратегий. Для иллюстрации отметим, что паре  ,
маркированной темной точкой на левом фрагменте рис. 2.10, соответствуют смешанная
стратегия (x*,1-x*)=(0,1) первой стороны и смешанная
стратегия (y*,1-y*)=(1,0) второй стороны. Устойчивые решения такого
типа реализуемы и в чистых стратегиях.
,
маркированной темной точкой на левом фрагменте рис. 2.10, соответствуют смешанная
стратегия (x*,1-x*)=(0,1) первой стороны и смешанная
стратегия (y*,1-y*)=(1,0) второй стороны. Устойчивые решения такого
типа реализуемы и в чистых стратегиях.
Пример, рассмотренный в "Нормальная форма конечной игры. Задание конечной игры в позиционной форме" (соглашение об ограничении лова рыбы), иллюстрирует этот случай. Используя выражения (10.6) и (10.8), получаем (в соответствии со значениями элементов матриц, соответствующих примеру), что A=B=0 и a=b=1. Этим значениям соответствуют левые верхние фрагменты на рис. 2.8 и рис. 2.9. Следовательно, задача имеет единственное устойчивое решение
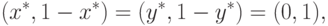
Ситуация, когда  игра не имеет устойчивых решений в
чистых стратегиях,
но обретает такое решение в смешанных стратегиях, соответствует второму
случаю из пункта, завершающего доказательство теоремы. Устойчивое решение
в смешанных стратегиях окажется единственным, если решениями
систем (10.10) и (10.11) являются лишь точки трехзвенных ломаных линий,
соединяющих концы разных
диагоналей квадрата. При этом единственная устойчивая
пара стратегий
игра не имеет устойчивых решений в
чистых стратегиях,
но обретает такое решение в смешанных стратегиях, соответствует второму
случаю из пункта, завершающего доказательство теоремы. Устойчивое решение
в смешанных стратегиях окажется единственным, если решениями
систем (10.10) и (10.11) являются лишь точки трехзвенных ломаных линий,
соединяющих концы разных
диагоналей квадрата. При этом единственная устойчивая
пара стратегий
 |
( 11.1) |
 ,
в которой пересекаются указанные выше ломаные линии. В этом случае
,
в которой пересекаются указанные выше ломаные линии. В этом случае |
( 11.2) |
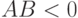 |
( 11.3) |
Неравенства (11.2)
для величин  и
и  из (10.19),
(10.20), определяемых соответственно коэффициентами a, A
из (10.6) и b, B из (10.8),
имеют следствием отношения
из (10.19),
(10.20), определяемых соответственно коэффициентами a, A
из (10.6) и b, B из (10.8),
имеют следствием отношения
 |
( 11.4) |
Оптимальные смешанные стратегии в 2 x 2 матричной игре
Как уже отмечалось, антагонистическому случаю соответствуют условия (8.2), согласно которым для величин из (10.6) и (10.8) справедливы отношения
 |
( 11.5) |
При этом
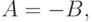 |
( 11.6) |
 матрицы игры (см. определение в
"Нормальная форма конечной игры. Задание конечной игры в позиционной форме"
), поскольку совпадение
значений коэффициентов в любой строке (или в столбце)
матрицы игры (см. определение в
"Нормальная форма конечной игры. Задание конечной игры в позиционной форме"
), поскольку совпадение
значений коэффициентов в любой строке (или в столбце)  матрицы гарантирует существование такого значения. Таким образом, в
матрицы гарантирует существование такого значения. Таким образом, в  антагонистической игре отсутствие устойчивых решений в чистых стратегиях
гарантирует существование единственного устойчивого решения
в смешанных стратегиях, порождаемого
парой
антагонистической игре отсутствие устойчивых решений в чистых стратегиях
гарантирует существование единственного устойчивого решения
в смешанных стратегиях, порождаемого
парой 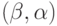 , где
, где
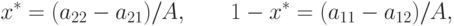 |
( 11.7) |
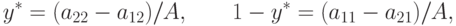 |
( 11.8) |
![\begin{multiline}
(\forall y \in [0,1])\, M(x^\ast, y) = \{[a_{11}
(a_{22} - a_{21}) + a_{21}(a_{11} - a_{12})] \cdot y +\\
+ [a_{12} (a_{22} - a_{21}) +
a_{22}(a_{11} - a_{12})](1 -y)\}/A =\\
= (a_{11}a_{22} - a_{12}a_{21})/A = M(x^\ast, y^\ast).
\end{multiline}](/sites/default/files/tex_cache/101a1c56422c1cc50baa10c0c51e10cb.png) |
( 11.9) |
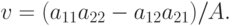 |
( 11.10) |
Отметим одно важное обстоятельство. Из (11.9), (11.10) следует, что
![(\forall y \in [0,1])\, M(x^\ast, y) = v.](/sites/default/files/tex_cache/6fb19cfa146d6d39ccc5c0ce85cd4767.png)
Аналогично можно получить симметричное утверждение
![(\forall x \in [0,1])\, M(x, y^\ast) = v.](/sites/default/files/tex_cache/0dcebb7c0c24bc3f6221eb724d1c1f5a.png)
 матрицы игры.
Пусть одна из сторон (заведомо) использует рулетку, реализующую оптимальную смесь чистых
стратегий. Тогда, независимо от того, какую стратегию выбирает другая
сторона, ее ожидаемый выигрыш совпадает с ценой игры. Т.е. любая
ее стратегия обеспечивает максимальный гарантированный уровень
математического ожидания выигрыша (величину v для стороны P1 и величину ( -v для стороны P2 ).
матрицы игры.
Пусть одна из сторон (заведомо) использует рулетку, реализующую оптимальную смесь чистых
стратегий. Тогда, независимо от того, какую стратегию выбирает другая
сторона, ее ожидаемый выигрыш совпадает с ценой игры. Т.е. любая
ее стратегия обеспечивает максимальный гарантированный уровень
математического ожидания выигрыша (величину v для стороны P1 и величину ( -v для стороны P2 ).Согласно выражениям (11.7), (11.8) и (11.10), рассмотренный ранее пример рекламной борьбы (см. "Смешанные стратегии и проблема устойчивости решений" ), не имеющий устойчивых решений в чистых стратегиях, имеет единственное устойчивое решение в смешанных стратегиях:
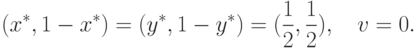
Теперь вернемся к примеру погони за конкурентом, в котором при отсутствии
полной информации (см. дерево игры на рис. 2.5) нет устойчивых решений в
чистых стратегиях (см. также замечание 2.2 в
"Приведение позиционной игры к игре в нормальной форме.
Условия существования стратегического равновесия"
). Обратимся
к соответствующей этому случаю матрице  матрице игры,
приведенной в
"Приведение позиционной игры к игре в нормальной форме.
Условия существования стратегического равновесия"
. Заметим, что первая
и вторая стратегии стороны P1 дают одни
и те же выигрыши против одной и той же стратегии стороны P2. При
этом третья стратегия стороны P1 даже превосходит ее четвертую
стратегию. Фактически, мы имеем ситуацию, когда каждый элемент матрицы, находящийся
в строке с номером i, превышает соответствующий (т.е. находящийся
в том же столбце) элемент из строки с номером k (или хотя бы не
меньше, чем этот элемент):
матрице игры,
приведенной в
"Приведение позиционной игры к игре в нормальной форме.
Условия существования стратегического равновесия"
. Заметим, что первая
и вторая стратегии стороны P1 дают одни
и те же выигрыши против одной и той же стратегии стороны P2. При
этом третья стратегия стороны P1 даже превосходит ее четвертую
стратегию. Фактически, мы имеем ситуацию, когда каждый элемент матрицы, находящийся
в строке с номером i, превышает соответствующий (т.е. находящийся
в том же столбце) элемент из строки с номером k (или хотя бы не
меньше, чем этот элемент):
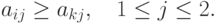
 матрицей:
матрицей:| Редуцированная матрица игры | Смешанная cтратегия P2 | ||
| 1/6 | 5/6 | ||
| Смешанная стратегия P1 | 2/3 | 2 | 4 |
| 1/3 | 7 | 3 | |
Согласно (11.7), (11.8) и (11.10), этой игре соответствует устойчивое (и эффективное) решение в смешанных стратегиях вида:
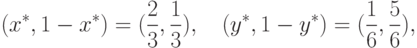
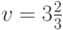 .
Примем, что первая и четвертая (чистые) стратегии
в исходной
.
Примем, что первая и четвертая (чистые) стратегии
в исходной  игре используются первым игроком с нулевыми
вероятностями. Тогда случайный механизм, характеризуемый вектором
вероятностей
игре используются первым игроком с нулевыми
вероятностями. Тогда случайный механизм, характеризуемый вектором
вероятностей 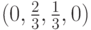 ,
обеспечивает игроку P1 математическое ожидание выигрыша, равное
указанной выше цене
,
обеспечивает игроку P1 математическое ожидание выигрыша, равное
указанной выше цене 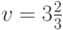 . Фактически, обсуждая этот
пример, мы обобщили смешанные стратегии на случай, когда число чистых стратегий
превышает 2. Более последовательное рассмотрение такого обобщения будет
проведено ниже.
. Фактически, обсуждая этот
пример, мы обобщили смешанные стратегии на случай, когда число чистых стратегий
превышает 2. Более последовательное рассмотрение такого обобщения будет
проведено ниже.Замечание 2.5 (о природе устойчивости решений в антагонистической игре) Если изменить знаки всех элементов матрицы игры на противоположные, то, согласно (11.10), знак цены игры также изменится. Например, если значение цены игры было положительным (в этом случае говорят, что игра поставлена в пользу первого игрока), то оно изменится на отрицательное значение (т.е. игра будет поставлена уже в пользу второго игрока). Однако пара устойчивых смешанных стратегий, определяемых выражениями (10.7) и (10.8), останется неизменной.
