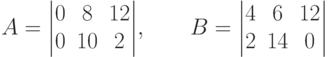|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Сделки без побочных платежей
Пример 3.1. Рассмотрим  биматричную игру с матрицами из
табл. 3.1. Допустимое множество S
для этого примера построено
на рис. 3.3 как многоугольник.
Вершины этого многоугольника принадлежат
множеству (14.1), соответствующему матрицам из
табл. 3.1. Точки, соответствующие вершинам
многоугольника S, отмечены на рисунке темными кружками.
биматричную игру с матрицами из
табл. 3.1. Допустимое множество S
для этого примера построено
на рис. 3.3 как многоугольник.
Вершины этого многоугольника принадлежат
множеству (14.1), соответствующему матрицам из
табл. 3.1. Точки, соответствующие вершинам
многоугольника S, отмечены на рисунке темными кружками.
Согласно (14.7), (14.8) и (14.10), (14.11) рассматриваемый пример
характеризуется значениями3Заметим, что матрица A
содержит седловое значение, а в матрице  второй столбец доминирует первый
и, следовательно, получение оценок для второго игрока сводится к анализу
второй столбец доминирует первый
и, следовательно, получение оценок для второго игрока сводится к анализу  матрицы.
матрицы.

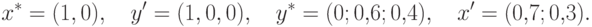
 ,
а точка
,
а точка 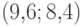 из (14.14), соответствующая
рулетке
из (14.14), соответствующая
рулетке  из (14.13), принадлежит границе
допустимого множества.
из (14.13), принадлежит границе
допустимого множества.Первое предположение Нэша состоит в том, что стороны P1 и P2 будут согласовывать лишь сделки  ,
удовлетворяющие неравенствам
,
удовлетворяющие неравенствам

 |
( 14.15) |
 |
( 14.16) |
Следующее условие ( аксиома неулучшаемости или оптимальности по Парето), введенное Нэшем, отражает то обстоятельство, что обе стороны проявят готовность рассматривать варианты, повышающие выигрыш каждой из них. Поэтому сделка, принимаемая окончательно, должна быть уже неулучшаема (см. определение в "Устойчивость и эффективность поведения сторон: совместимость свойств устойчивости и эффективности" ). Мы будем записывать это условие в следующей форме
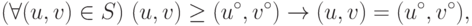 |
( 14.17) |
Формулировки двух следующих условий Нэша предполагают, что
сделка  , согласуемая сторонами,
может быть определена как некоторая функция
, согласуемая сторонами,
может быть определена как некоторая функция
 |
( 14.18) |
 , аргументами которого являются допустимое
множество S и выигрыши u*,v*, гарантируемые
односторонними действиями соответственно P1 и P2.
Предположение (14.18) фактически означает, что оператор
, аргументами которого являются допустимое
множество S и выигрыши u*,v*, гарантируемые
односторонними действиями соответственно P1 и P2.
Предположение (14.18) фактически означает, что оператор  (ниже мы установим
его существование) является моделью формирования
сделки. Заметим также, что излагаемая ниже теория справедлива для любого
выпуклого, ограниченного и замкнутого множества S и пары уровней u*,v* доминируемых какой-либо точкой из S.
Т.е. величины S и u*, v*,
соответственно, из (14.6), (14.7) и (14.12), связанные с некоторой
(ниже мы установим
его существование) является моделью формирования
сделки. Заметим также, что излагаемая ниже теория справедлива для любого
выпуклого, ограниченного и замкнутого множества S и пары уровней u*,v* доминируемых какой-либо точкой из S.
Т.е. величины S и u*, v*,
соответственно, из (14.6), (14.7) и (14.12), связанные с некоторой  биматричной игрой, можно интерпретировать как (основной в нашем рассмотрении) частный случай.
биматричной игрой, можно интерпретировать как (основной в нашем рассмотрении) частный случай.Теперь введем четвертое условие Нэша, утверждающее, что согласованная
сторонами сделка  сохраняется при усечении
исходного множества S до некоторого подмножества
сохраняется при усечении
исходного множества S до некоторого подмножества 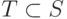 ,
включающего эту сделку. Эту аксиому независимости от посторонних
альтернатив можно записать в следующем виде:
,
включающего эту сделку. Эту аксиому независимости от посторонних
альтернатив можно записать в следующем виде:
![[(u^\circ, v^\circ) \!\in\! T \!\subset\! S] \& [(u^\circ, v^\circ) \!=\!
\varphi(S, u^\ast, v^\ast)] \!\to\! (u^\circ, v^\circ) \!=\!
\varphi(T, u^\ast, v^\ast).](/sites/default/files/tex_cache/f5074c8950db6c02127a5cdcf700f6b5.png) |
( 14.19) |
Сформулируем пятое условие, называемое аксиомой независимости от линейного преобразования. Введем линейное преобразование шкал полезностей сторон вида:
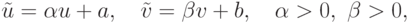 |
( 14.20) |
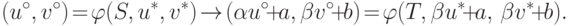 |
( 14.21) |
Последнее условие ( аксиома симметрии ) имеет вид следствия:
![[u^\ast = v^\ast] \& [(u,v) \in S \leftrightarrow
(v,u) \in S] \to u^\circ = v^\circ.](/sites/default/files/tex_cache/f3a4bfa21593608ebe73e116c12d67dd.png) |
( 14.22) |
 , должны совпадать. Можно
интерпретировать это предположение как признание невозможности увеличения
своего выигрыша по сравнению с выигрышем партнера, если ресурсы сторон,
отражаемые симметричным множеством S и совпадающими
гарантированными уровнями u*,v*,
являются в некотором роде одинаковыми.
Разумеется, эти три аргумента оператора
, должны совпадать. Можно
интерпретировать это предположение как признание невозможности увеличения
своего выигрыша по сравнению с выигрышем партнера, если ресурсы сторон,
отражаемые симметричным множеством S и совпадающими
гарантированными уровнями u*,v*,
являются в некотором роде одинаковыми.
Разумеется, эти три аргумента оператора  из (14.18)
не описывают всех (могущих встретиться в практике переговоров) аспектов
взаимоотношений сторон при согласовании
сделки. Поэтому условие (14.22) можно интерпретировать и как некоторое нормативное
определение справедливости.
из (14.18)
не описывают всех (могущих встретиться в практике переговоров) аспектов
взаимоотношений сторон при согласовании
сделки. Поэтому условие (14.22) можно интерпретировать и как некоторое нормативное
определение справедливости.Замечание 3.2 (о дележах ). Любая допустимая, индивидуально рациональная сделка, удовлетворяющая условию (14.17), может рассматриваться как некоторое (не улучшаемое одновременно для обеих сторон) распределение полезности в исходе операции. Поэтому сделки, удовлетворяющие условиям (14.15)-(14.17), называют дележами.