|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Целозначные многочлены и размерностные многочлены матриц и подмножеств в Nm
12.6. ОПРЕДЕЛЕНИЕ.
Многочлен  , существование которого доказано в теореме
12.5, называется
"многочленом Гильберта" подмножества
, существование которого доказано в теореме
12.5, называется
"многочленом Гильберта" подмножества 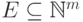 .
.
12.7. ЗАМЕЧАНИЕ.
Из рассуждений, приведенных в начале доказательства теоремы 12.5, следует,
что размерностный многочлен множества 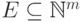 равен
размерностному многочлену конечного множества
равен
размерностному многочлену конечного множества  , состоящего из
всех минимальных элементов множества
, состоящего из
всех минимальных элементов множества  .
Поэтому, чтобы уметь находить размерностные многочлены подмножеств
множества
.
Поэтому, чтобы уметь находить размерностные многочлены подмножеств
множества  , достаточно найти метод, вычисляющий размерностные
многочлены конечных подмножеств
, достаточно найти метод, вычисляющий размерностные
многочлены конечных подмножеств 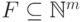 , элементы которых
попарно несравнимы.
, элементы которых
попарно несравнимы.
Поэтому в дальнейшем мы всегда будем иметь дело с конечными
множествами 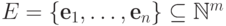 и записывать элементы этих множеств
в виде матрицы размера
и записывать элементы этих множеств
в виде матрицы размера 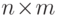 со
строками
со
строками 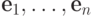 .
Эту матрицу будем обозначать той же буквой
.
Эту матрицу будем обозначать той же буквой  . Под размерностным
многочленом
. Под размерностным
многочленом 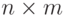 -матрицы
-матрицы  мы будем понимать
размерностный многочлен множества строк матрицы
мы будем понимать
размерностный многочлен множества строк матрицы  (рассматриваемого
как подмножество множества
(рассматриваемого
как подмножество множества  ). В следующей теореме мы
формулируем
уже доказанные свойства размерностных многочленов подмножеств
множества
). В следующей теореме мы
формулируем
уже доказанные свойства размерностных многочленов подмножеств
множества  в форме свойств размерностных многочленов матриц.
Все элементы рассматриваемых матриц и векторов принадлежат
в форме свойств размерностных многочленов матриц.
Все элементы рассматриваемых матриц и векторов принадлежат 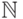 .
.
12.8. ТЕОРЕМА. Предположим, что 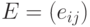 -
- 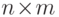 -матрица и
-матрица и 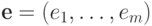 - вектор. Тогда
- вектор. Тогда
- имеет место равенствогде
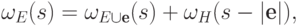
( 12.3) 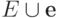 - матрица, полученная присоединением
строки
- матрица, полученная присоединением
строки  к
матрице
к
матрице  ,
, 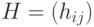 -
- 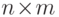 -матрица с элементами
-матрица с элементами 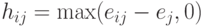 ,
, 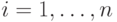 ,
, 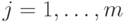 , и
, и 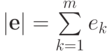 ;
; -
если
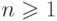 , тогде
, тогде
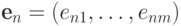 , и
, и 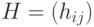 - это
- это 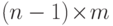 -матрица, такая,
что
-матрица, такая,
что  ;
; -
размерностный многочлен матрицы
 не меняется при перестановке
строк;
не меняется при перестановке
строк;
-
размерностный многочлен матрицы
 не меняется при перестановке
столбцов матрицы
не меняется при перестановке
столбцов матрицы  ;
; - если
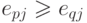 при
при 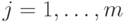 ,
то
,
то 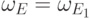 , где матрица
, где матрица  получена
из
получена
из  удалением
удалением  -й строки
(такую строку мы называем лишней
);
-й строки
(такую строку мы называем лишней
); -
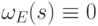 тогда и только тогда,
когда
тогда и только тогда,
когда  содержит нулевую строку (в этом случае
полагаем
содержит нулевую строку (в этом случае
полагаем 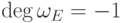 );
); -
если
 непусто, т. е. содержит хотя бы одну строку, то
непусто, т. е. содержит хотя бы одну строку, то 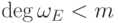 ; размерностный многочлен "пустой" матрицы
равен
; размерностный многочлен "пустой" матрицы
равен  ;
; -
если
 содержит строку
содержит строку 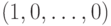 ,
то
,
то 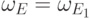 , где
, где 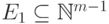 - матрица,
полученная из
- матрица,
полученная из  удалением
сначала строк, первая координата которых больше 0, а затем первого столбца
(состоящего из нулей).
В частности, если
удалением
сначала строк, первая координата которых больше 0, а затем первого столбца
(состоящего из нулей).
В частности, если  содержит строку
содержит строку 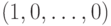 и в
первом столбце имеется нулевой элемент, то
и в
первом столбце имеется нулевой элемент, то 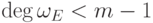 ;
; -
если
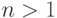 и
и 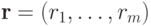 , где
, где 
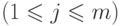 , тогде
, тогде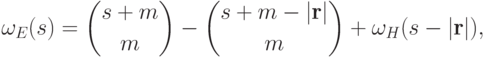
 -
- 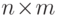 -матрица, полученная
вычитанием вектора
-матрица, полученная
вычитанием вектора 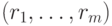 из каждой строки
матрицы
из каждой строки
матрицы  (в частности, каждый столбец
матрицы H содержит 0 ).
(в частности, каждый столбец
матрицы H содержит 0 ).
Фиксируем 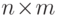 -матрицу
-матрицу  со
строками
со
строками 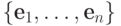 . Для
вычисления
. Для
вычисления  можно применить соотношение (12.3),
выбирая строки матрицы
можно применить соотношение (12.3),
выбирая строки матрицы  случайным образом; эта процедура приводит
к комбинаторной формуле (12.4),
дающей явное выражение для
случайным образом; эта процедура приводит
к комбинаторной формуле (12.4),
дающей явное выражение для  .
.
Для более точной формулировки введем некоторые обозначения.
Пусть 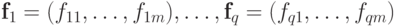 элементы множества
элементы множества  . Тогда элемент
. Тогда элемент 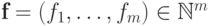 , где
, где 
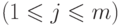 называется наименьшим общим кратным элементов
называется наименьшим общим кратным элементов 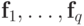 и
обозначается
и
обозначается 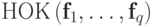 .
Для любых
.
Для любых  , таких, что
, таких, что 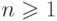 ,
, 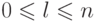 , обозначим через
, обозначим через 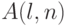 множество
всех
множество
всех  -элементных подмножеств
множества
-элементных подмножеств
множества 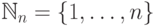 , и для любого
, и для любого  положим
положим  . Далее,
обозначим
. Далее,
обозначим 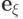 наименьшее общее кратное
элементов множества
наименьшее общее кратное
элементов множества 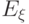 (как и прежде, элементы
множества
(как и прежде, элементы
множества  сравниваются относительно порядка произведения
"
сравниваются относительно порядка произведения
"  ", если противное не оговорено явно).
Если
", если противное не оговорено явно).
Если 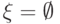 , то
, то 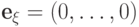 ;
если
;
если 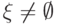 , то, очевидно,
, то, очевидно, 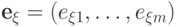 , где
, где 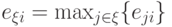
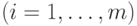 .
Пусть
.
Пусть 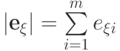 .
.
12.9. ПРЕДЛОЖЕНИЕ. В обозначениях, введенных выше, следующее соотношение имеет место
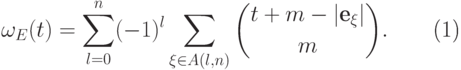 |
( 12.4) |
ДОКАЗАТЕЛЬСТВО.
Воспользуемся индукцией по  . Случай
. Случай 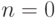 следует из
теоремы 12.8.
следует из
теоремы 12.8.
Если  , то по формуле (12.3) имеем
, то по формуле (12.3) имеем
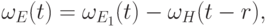
 обозначает
обозначает 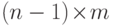 -матрицу,
полученную из
-матрицу,
полученную из  удалением последней
строки,
удалением последней
строки, 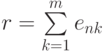 , и
, и 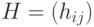 ,
где
,
где  ,
,  ,
, 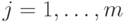 . По предположению индукции
. По предположению индукции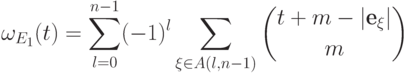
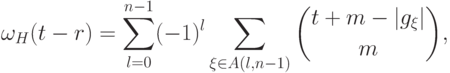
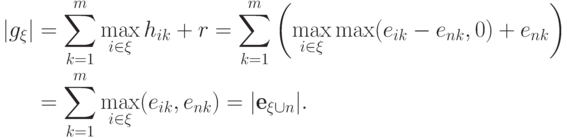
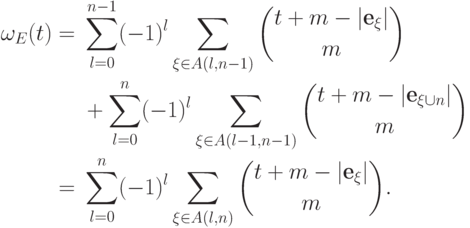
Предложение 12.9, в частности,
означает, что многочлен Гильберта
множества  представляется в виде
представляется в виде
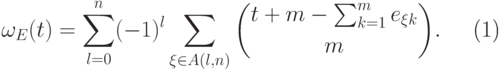 |
( 12.5) |
