|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Целозначные многочлены и размерностные многочлены матриц и подмножеств в Nm
Размерностные многочлены подмножеств в Nm. Размерностный многочлен матрицы
Пусть  - упорядоченные
множества. Их прямое произведение
- упорядоченные
множества. Их прямое произведение  можно упорядочить различными
способами. В основном мы будем рассматривать два отношения
порядка на множестве
можно упорядочить различными
способами. В основном мы будем рассматривать два отношения
порядка на множестве  : порядок произведения
: порядок произведения  ,
в котором неравенство
,
в котором неравенство  выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда  для всех
для всех 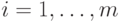 , и лексикографический порядок
, и лексикографический порядок 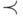 , который определяется следующими условиями:
, который определяется следующими условиями:  в
в  , если существует индекс
, если существует индекс  , такой, что
, такой, что 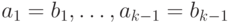 , но
, но  ,
,  . Легко видеть, что если
каждое множество
. Легко видеть, что если
каждое множество 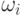
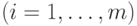 вполне упорядочено относительно порядка
вполне упорядочено относительно порядка  , то множество
, то множество  является вполне упорядоченным
относительно лексикографического порядка
(в общем случае,
является вполне упорядоченным
относительно лексикографического порядка
(в общем случае,  не является даже линейно упорядоченным
относительно порядка произведения).
не является даже линейно упорядоченным
относительно порядка произведения).
Мы будем рассматривать порядок произведения  и лексикографический порядок
и лексикографический порядок 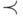 на множестве
на множестве  всех
всех  -мерных векторов с неотрицательными целыми координатами, а также
на множествах вида
-мерных векторов с неотрицательными целыми координатами, а также
на множествах вида 
 , где
, где  для любого
для любого 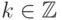 ,
,  . Множества
. Множества 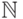 и
и  всегда рассматриваются
с естественным порядком, относительно которого
они, очевидно, вполне упорядочены.
Этот естественный порядок мы будем обозначать тем же символом
всегда рассматриваются
с естественным порядком, относительно которого
они, очевидно, вполне упорядочены.
Этот естественный порядок мы будем обозначать тем же символом  , который используется для обозначения порядка произведения,
если это не ведет к неоднозначности толкования.
, который используется для обозначения порядка произведения,
если это не ведет к неоднозначности толкования.
12.1. ЛЕММА.
-
Любое бесконечное подмножество множества

 с одержит бесконечную последовательность, строго возрастающую
относительно порядка произведения,
проекции всех элементов которой на
с одержит бесконечную последовательность, строго возрастающую
относительно порядка произведения,
проекции всех элементов которой на  равны между
собой.
равны между
собой. -
Существует упорядочение
 множества
множества  , относительно которого это множество
является вполне упорядоченным, удовлетворяющее следующим двум условиям:
, относительно которого это множество
является вполне упорядоченным, удовлетворяющее следующим двум условиям:-

 для всех
для всех
-
если

 , тодля всех
, тодля всех
 ,
,  .
. -
Множество
 является вполне упорядоченным
относительно любого линейного порядка,
удовлетворяющего условию 2a.
является вполне упорядоченным
относительно любого линейного порядка,
удовлетворяющего условию 2a.
-
ДОКАЗАТЕЛЬСТВО.
Легко видеть, что если  - бесконечное подмножество
множества
- бесконечное подмножество
множества  , то
существует бесконечное подмножество
, то
существует бесконечное подмножество 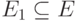 , проекции всех
элементов
, проекции всех
элементов  которого на
которого на  равны между собой. Значит,
для доказательства первого утверждения леммы
достаточно показать, что любое бесконечное подмножество
в
равны между собой. Значит,
для доказательства первого утверждения леммы
достаточно показать, что любое бесконечное подмножество
в  содержит бесконечную последовательность, строго
возрастающую относительно порядка произведения.
Пусть
содержит бесконечную последовательность, строго
возрастающую относительно порядка произведения.
Пусть  - бесконечное подмножество множества
- бесконечное подмножество множества  . Если множество первых координат элементов множества
. Если множество первых координат элементов множества  бесконечно, то существует бесконечное подмножество
бесконечно, то существует бесконечное подмножество  , первые координаты любых двух различных элементов
которого различны.
Значит, существует бесконечная последовательность
, первые координаты любых двух различных элементов
которого различны.
Значит, существует бесконечная последовательность  , такая, что первые координаты элементов из
, такая, что первые координаты элементов из 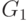 образуют строго возрастающую
последовательность в
образуют строго возрастающую
последовательность в 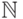 . Если же множество первых координат
элементов из
. Если же множество первых координат
элементов из  конечно, то существует бесконечное подмножество
конечно, то существует бесконечное подмножество  , все элементы которого имеют одну и ту же первую
координату. В обоих случаях
существует бесконечная подпоследовательность
, все элементы которого имеют одну и ту же первую
координату. В обоих случаях
существует бесконечная подпоследовательность  ,
состоящая из различных элементов
множества
,
состоящая из различных элементов
множества  , первые координаты которых образуют неубывающую
последовательность в
, первые координаты которых образуют неубывающую
последовательность в 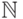 . Аналогично, из
. Аналогично, из 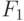 можно выбрать бесконечную
подпоследовательность
можно выбрать бесконечную
подпоследовательность 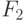 , вторые координаты элементов которой образуют неубывающую
последовательность
в
, вторые координаты элементов которой образуют неубывающую
последовательность
в 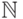 и т.д. В результате мы получим бесконечную последовательность
и т.д. В результате мы получим бесконечную последовательность  элементов из
элементов из  , которая строго возрастает
относительно порядка произведения. Таким образом,
первое утверждение леммы доказано.
, которая строго возрастает
относительно порядка произведения. Таким образом,
первое утверждение леммы доказано.
Рассмотрим порядок  на множестве
на множестве  , такой, что
, такой, что


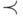 " обозначает лексикографический порядок на
" обозначает лексикографический порядок на  ) для любых элементов
) для любых элементов  ,
, 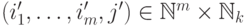 . Множество
. Множество  вполне упорядочено относительно этого порядка
(поскольку множество
вполне упорядочено относительно этого порядка
(поскольку множество  вполне упорядочено относительно
лексикографического порядка),
и условия 2a и 2b, очевидно, выполнены.
вполне упорядочено относительно
лексикографического порядка),
и условия 2a и 2b, очевидно, выполнены.Докажем последнее утверждение леммы. Пусть  -
линейный порядок на множестве
-
линейный порядок на множестве  , удовлетворяющий условию 2a, и пусть
, удовлетворяющий условию 2a, и пусть  - бесконечное
подмножество множества
- бесконечное
подмножество множества  . По первому утверждению
леммы, существует бесконечная
подпоследовательность
. По первому утверждению
леммы, существует бесконечная
подпоследовательность  , строго возрастающая
относительно порядка произведения
и такая, что проекции на
, строго возрастающая
относительно порядка произведения
и такая, что проекции на  всех ее элементов равны между собой.
Покажем, что
всех ее элементов равны между собой.
Покажем, что 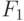 также строго возрастает относительно порядка
также строго возрастает относительно порядка  . Действительно, если
. Действительно, если  ,
,  и
и  ,
,  , то
, то  , поскольку порядок
, поскольку порядок  удовлетворяет условию 2a. Таким
образом, любая строго убывающая (относительно порядка
удовлетворяет условию 2a. Таким
образом, любая строго убывающая (относительно порядка  ) последовательность элементов из
) последовательность элементов из  конечна (иначе, как мы видели,
она содержит строго возрастающую последовательность, что невозможно для
убывающей последовательности),
так что множество
конечна (иначе, как мы видели,
она содержит строго возрастающую последовательность, что невозможно для
убывающей последовательности),
так что множество  вполне упорядочено. Лемма доказана.
вполне упорядочено. Лемма доказана.
Пусть  и
и  - подмножество
множества
- подмножество
множества  . Для любого
. Для любого  обозначим
обозначим  множество элементов
множество элементов  из
из  , для которых выполнено
неравенство
, для которых выполнено
неравенство  .
.
Если  , то
, то 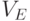 будет обозначать множество всех
элементов
будет обозначать множество всех
элементов  , которые не превосходят ни одного элемента из
, которые не превосходят ни одного элемента из  относительно порядка произведения
относительно порядка произведения  на
на  . (В дальнейшем, если противное не
оговорено явно, все сравнения элементов из
. (В дальнейшем, если противное не
оговорено явно, все сравнения элементов из  рассматриваются относительно порядка произведения.) Таким
образом, включение
рассматриваются относительно порядка произведения.) Таким
образом, включение  эквивалентно утверждению, что неравенство
эквивалентно утверждению, что неравенство  не выполняется ни для какого
не выполняется ни для какого  .
.
В дальнейшем  обозначает функцию
обозначает функцию  ,
такую, что
,
такую, что  для любого
для любого  .
.
