Предмет вычислительной математики. Обусловленность задачи, устойчивость алгоритма, погрешности вычислений. Задача численного дифференцирования
1.6. Задача численного дифференцирования
В пункте "1.2" уже была введена простейшая формула численного дифференцирования. Рассмотрим задачу приближенного вычисления значения производной подробнее.
Пусть задана таблица значений xi. В дальнейшем совокупность точек на отрезке, на котором проводятся вычисления, иногда будут называться сеткой, каждое значение xi — узлом сетки. Пусть сетка — равномерная, и расстояние между узлами равно h — шагу сетки. Пусть узлы сетки пронумерованы в порядке возрастания, т.е.
x0 = a, xj = a + jh,, j = 0, 1, ... , N
Пусть f(xj) = fj — функция, определенная в узлах сетки. Такие функции будут называться табличными, или сеточными функциями. Считаем, кроме того, что рассматриваемая сеточная функция есть проекция (или ограничение) на сетку некоторой гладкой нужное число раз непрерывно дифференцируемой функции f(x). По определению производной

тогда, если шаг сетки достаточно мал, по аналогии можно написать формулу в конечных разностях, дающую приближенное значение производной сеточной функции:
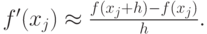 |
( 1.1) |
Если параметр h достаточно мал, то можно считать полученное значение производной достаточно точным. Погрешность формулы (1.1) оценена в пункте
"1.2"
. Как показано выше, при уменьшении шага сетки h ошибка будет уменьшаться, но при некотором значении h ошибка может возрасти до бесконечности. При оценке погрешности метода обычно считается, что все вычисления были точными. Но существует ошибка округления.
При оценке ее большую роль играет машинный  —
мера относительной погрешности машинного округления, возникающей из-за конечной разрядности мантиссы при работе с числами в формате с плавающей точкой. Напомним, что по определению машинным
—
мера относительной погрешности машинного округления, возникающей из-за конечной разрядности мантиссы при работе с числами в формате с плавающей точкой. Напомним, что по определению машинным  называют наибольшее из чисел, для которых в рамках используемой системы вычислений выполнено
называют наибольшее из чисел, для которых в рамках используемой системы вычислений выполнено 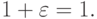 Тогда абсолютная погрешность при вычислении значения функции (или представлении табличной функции) есть
Тогда абсолютная погрешность при вычислении значения функции (или представлении табличной функции) есть  Максимальный вклад погрешностей округления при вычислении производной по формуле (1.1) будет
Максимальный вклад погрешностей округления при вычислении производной по формуле (1.1) будет
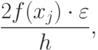
Пусть k = max |f(x)|, максимум ищется на отрезке, на котором вычисляются значения производных. Тогда суммарная ошибка, состоящая из погрешности метода и погрешности округления, есть
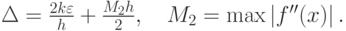
Для вычисления оптимального шага численного дифференцирования найдем минимум суммарной ошибки, как функции шага сетки


Если требуется повысить точность вычисления производных, необходимо воспользоваться формулами, имеющими меньшие погрешности метода. Так, из курсов математического анализа известно, что
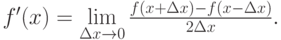
По аналогии напишем конечно-разностную формулу
 |
( 1.2) |
(1.2) — формула с центральной разностью. Исследуем ее на аппроксимацию, т.е. оценим погрешность метода. Предположим, что функция, которую спроектировали на сетку, трижды непрерывно дифференцируема, тогда

Погрешность метода определяется 3-й производной функции. Введем ![M_3 = \max\limits_{x \in [a,b]} \left|{f^{\prime\prime\prime}(x)}\right|](/sites/default/files/tex_cache/24050e188589fa68d8867c8dae145492.png) , тогда суммарная погрешность при вычислении по формуле с центральной разностью есть
, тогда суммарная погрешность при вычислении по формуле с центральной разностью есть

для вычисления оптимального шага, находя минимум погрешности, как функции шага сетки, имеем

![$ h_{opt} = \sqrt[3]{\frac{3k\varepsilon }{M_3}}$.](/sites/default/files/tex_cache/fd4fab42340b0e41d8644a0960d9f769.png)
Для более точного вычисления производной необходимо использовать разложение более высокого порядка, шаг hopt будет увеличиваться.
Формула (1.1) — двухточечная, (1.2) — трехточечная: при вычислении производной используются точки (узлы) xj (узел входит с нулевым коэффициентом), xj + h, xj - h — совокупность узлов, участвующих в каждом вычислении производной, в дальнейшем будем иногда называть сеточным шаблоном.
Введем на рассматриваемом отрезке шаблон из нескольких точек.
Считаем, что сетка равномерная — шаг сетки постоянный, расстояния между любыми двумя соседними узлами равны. Используем для вычисления значения первой производной следующую приближенную (конечно-разностную) формулу:
 |
( 1.3) |
шаблон включает l точек слева от рассматриваемой точки xj и m справа. Коэффициенты  — неопределенные коэффициенты. Формула дифференцирования может быть и односторонней — либо l, либо m могут равняться нулю. В первом случае иногда называют (на наш взгляд, не слишком удачно) такую приближенную формулу формулой дифференцирования вперед, во втором — формулой дифференцирования назад. Потребуем, чтобы (1.3) приближала первую производную с точностью O(hl + m) . Используем разложения в ряд Тейлора в окрестности точки xj. Подставляя их в (1.3), получим
— неопределенные коэффициенты. Формула дифференцирования может быть и односторонней — либо l, либо m могут равняться нулю. В первом случае иногда называют (на наш взгляд, не слишком удачно) такую приближенную формулу формулой дифференцирования вперед, во втором — формулой дифференцирования назад. Потребуем, чтобы (1.3) приближала первую производную с точностью O(hl + m) . Используем разложения в ряд Тейлора в окрестности точки xj. Подставляя их в (1.3), получим

Потребуем выполнение условий:
 |
( 1.4) |
Получаем систему линейных алгебраических уравнений для неопределенных
коэффициентов  (1.4). Матрица этой системы есть
(1.4). Матрица этой системы есть
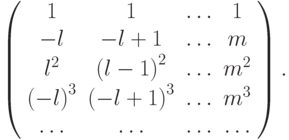
Вектор правых частей (0, 1, 0, ..., 0)T.
Определитель данной матрицы — детерминант Вандермонда. Из курса линейной алгебры следует, что он не равен нулю. Тогда существует единственный набор
коэффициентов  , который позволяет найти на шаблоне из (1 + l + m) точек значение первой производной с точностью O(hl + m).
, который позволяет найти на шаблоне из (1 + l + m) точек значение первой производной с точностью O(hl + m).
Для нахождения второй производной можно использовать ту же самую формулу (1.3) с небольшой модификацией

только теперь

Очевидно, что и данная система уравнений для нахождения неопределенных коэффициентов имеет единственное решение. Для получения с той же точностью приближенных значений производных до порядка l + m включительно с точностью O(hl + m) модификации формулы (1.3) и условий (1.4) очевидны, набор неопределенных коэффициентов находится единственным образом.
Таким образом, доказано следующее утверждение. На сеточном шаблоне, включающем в себя N + 1 точку, с помощью метода неопределенных коэффициентов всегда можно построить единственную формулу для вычисления производной от первого до n порядка включительно с точностью O(hN).
Утверждение доказано для равномерной сетки, но на случай произвольных расстояний между сеточными узлами обобщение проводится легко.
Так как на практике вычисления проводятся с конечной длиной мантиссы, то получить нулевую ошибку невозможно.
Читателям предлагается оценить значение оптимального шага при вычислениях по формулам типа (1.3) самостоятельно.
