Введение в вычислительную математику
[+]
Московский физико-технический институт
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3973 / 1245 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00
ISBN: 978-5-9556-0065-9
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Программист, Математик
Теги: beta, алгебра, алгоритмы, арифметика, вычисления, дифференциальные уравнения, курсы, линейная алгебра, матрица Якоби, метод трапеций, метод Эйлера, норма вектора, поиск, программирование, разделенные разности, разложение в ряд, системы нелинейных уравнений, спектральные задачи, таблицы бутчера, численное решение уравнений, элементы
Лекция 2:

Предмет вычислительной математики. Обусловленность задачи, устойчивость алгоритма, погрешности вычислений. Задача численного дифференцирования
A
|
версия для печати
< Лекция 1 || Лекция 2: 1234567 || Лекция 3 >

1.4. Погрешность метода

Оценим погрешность при вычислении первой производной при помощи соотношения:

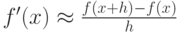
$ f^{\prime}(x) \approx \frac{f(x + h) - f(x)}{h} $
:

$ \frac {f(x + h ) - f(x)}{h} = \frac {[f(x) + hf^{\prime}(x) + O(h^2)] - f(x)}{h} = f^{\prime}(x) + O(h), $

где O(h) есть погрешность метода. В данном случае под погрешностью метода понимается абсолютная величина разности

$ \left|{f^{\prime}(x) - \frac{f(x + h) - f(x)}{h}}\right| $
, которая составляет O(h) (более точно
$ \frac{h}{2}f^{\prime\prime}(\xi ) $
, где \xi \in [x,x + h] ).

Если же взять другой метод вычисления производной

$ f^{\prime}(x) \approx \frac{f(x + h) - f(x - h)}{2h}$
, то получим, что его погрешность составляет O(h2), это оказывается существенным при малых h. Однако уменьшать h до бесконечности не имеет смысла, что видно из следующего примера. Реальная погрешность при вычислении первой производной будет

$ \Delta = \frac{h}{2} \max\limits_{\xi \in [x,x + h]} \left|{f^{\prime\prime}(\xi )}\right| + \frac{2\delta_M}{h} = O (h) + O(h^{- 1}), $

поскольку абсолютная погрешность вычисления значения функции за счет машинного округления не превосходит

$ \frac{2\delta_M}{h} $.

В этом случае можно найти оптимальный шаг h. Будем считать полную погрешность в вычислении производной \Delta функцией шага h. Отыщем минимум этой функции. Приравняв производную \Delta '_{h}(h) к нулю, получим оптимальный шаг численного дифференцирования

$ h_{\text{опт}} = 2\sqrt{\frac{\delta_M}{\max\limits_{\xi \in [x,x + h]} \left|{f^{\prime\prime}(\xi )}\right|}}. $

Выбирать значение h меньше оптимального не имеет смысла, так как при дальнейшем уменьшении шага суммарная погрешность начинает расти из-за возрастания вклада ошибок округления.

1.5. Элементы теории погрешностей

Определение. Пусть u и u* — точное и приближенное значение некоторой величины, соответственно. Тогда абсолютной погрешностью приближения u* называется величина 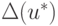\Delta (u^{*}), удовлетворяющая неравенству

\left|{u - u^*}\right| \le \Delta (u^*).

Определение. Относительной погрешностью называется величина \delta (u^*), удовлетворяющая неравенству

$ \left|{\frac{u - u^*}{u^*}}\right| \le \delta (u^*). $

Обычно используется запись u = u^*(1 \pm \delta (u^*)).

Определение. Пусть искомая величина u является функцией параметров t_1, \ldots t_n \in \Omega, u* — приближенное значение u. Тогда предельной абсолютной погрешностью называется величина

D(u^*) = \sup\limits_{(t_1, \ldots ,t_n) \in \Omega } \left|{u(t_1, \ldots ,t_n) - u^*}\right|,

Предельной относительной погрешностью называется величина D(u*)/| u*|.

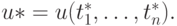Пусть \left|{t_j - t_j^*}\right| \le \Delta (t_j^* ), j = 1 \div n — приближенное значение u* = u(t_1^*, \ldots ,t_n^* ). Предполагаем, что u - непрерывно дифференцируемая функция своих аргументов. Тогда, по формуле Лагранжа,

u(t_1, \ldots ,t_n) - u^* = \sum\limits_{j = 1}^n \gamma_j (\alpha )(t_j - t_j^*),

где \gamma_j (\alpha ) = u'_{t_j}(t_1^* + \alpha (t_1 - t_1^*), \ldots ,t_n^* + \alpha (t_n - t_n^*)), 0 \le \alpha \le 1.

Отсюда

\left|{u(t_1, \ldots ,t_n) - u^*}\right| \le D_1 (u^*) = \sum\limits_{j = 1}^n b_j \Delta (t_j^*),
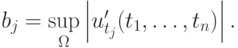
где b_j = \sup\limits_\Omega \left|{u^{\prime}_{t_j}(t_1, \ldots ,t_n)}\right|.

Можно показать, что при малых 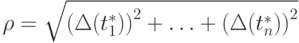\rho = \sqrt{{(\Delta (t_1^* ))}^2 + \ldots + {(\Delta (t_n^* ))}^2 } эта оценка не может быть существенно улучшена. На практике иногда пользуются грубой (линейной) оценкой

\left|{u(t_1, \ldots ,t_n) - u^*}\right| \le D_2 (u^*), \mbox{ где }D_2 (u^*) = \sum\limits_{j = 1} \left|{\gamma_j (0)}\right| \Delta (t^*).

Несложно показать, что

a) 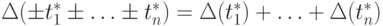\Delta ( \pm t_1^* \pm \ldots \pm t_n^*) = \Delta (t_1^* ) + \ldots + \Delta (t_n^* ) , предельная погрешность суммы или разности равна сумме предельных погрешностей.

b) Предельная относительная погрешность произведения или частного приближенного равна сумме предельных относительных погрешностей

\delta (t_1^* \cdots t_m^* \cdot d_1^{* - 1} \cdots d_m^{* - 1} ) = \delta (t_1^* ) + \ldots + \delta (t_m^*) + \delta (d_1^*) + \ldots + \delta (d_n^*).
Дальше >>
< Лекция 1 || Лекция 2: 1234567 || Лекция 3 >

Вопросы и ответы

вопросов: 1
Sanjar Ibrohimov
Sanjar Ibrohimov
ответить