| Россия, Новосибирск |
Арифметика Пресбургера
Теорема 37. Упорядоченные множества  и
и  (второе
состоит из двух копий множества
(второе
состоит из двух копий множества  , причем все элементы первой копии
считаются меньшими всех элементов второй копии) элементарно
эквивалентны как интерпретации сигнатуры
, причем все элементы первой копии
считаются меньшими всех элементов второй копии) элементарно
эквивалентны как интерпретации сигнатуры  .
.
Здесь также можно применить элиминацию кванторов, только надо добавить одноместные функции взятия последующего и предыдущего элементов. После этого надо заметить, что стандартная процедура элиминации кванторов (см. доказательство теоремы 29) состоит из преобразований, сохраняющих эквивалентность в обеих интерпретациях.
76. Можно ли построить счетную интерпретацию сигнатуры 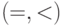 , в
которой равенство интерпретируется как совпадение элементов
(такие интерпретации называют нормальными), элементарно
эквивалентную множеству
, в
которой равенство интерпретируется как совпадение элементов
(такие интерпретации называют нормальными), элементарно
эквивалентную множеству  , но не изоморфную ему? Тот же
вопрос для множества неотрицательных рациональных чисел. Почему
существенна нормальность интерпретации?
, но не изоморфную ему? Тот же
вопрос для множества неотрицательных рациональных чисел. Почему
существенна нормальность интерпретации?
77. Существует ли упорядоченное множество, элементарно эквивалентное
упорядоченному множеству  , но имеющее большую мощность?
, но имеющее большую мощность?
78. Существуют ли два несчетных неизоморфных элементарно эквивалентных упорядоченных множества одинаковой мощности?
79. Будут ли упорядоченные множества  и
и  (пары целых чисел; сравниваются сначала вторые компоненты
пар, а при их равенстве — первые) изоморфны? элементарно эквивалентны?
(пары целых чисел; сравниваются сначала вторые компоненты
пар, а при их равенстве — первые) изоморфны? элементарно эквивалентны?
80. Будет ли упорядоченное множество  элементарно
эквивалентно
элементарно
эквивалентно 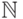 ? Будет ли
? Будет ли  элементарно
эквивалентно
элементарно
эквивалентно 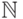 ?
?
Рассуждение, использованное при доказательстве теоремы
Тарского-Зайденберга, также можно приспособить для
доказательства элементарной эквивалентности. Сейчас мы
рассмотрим более простой случай алгебраически замкнутых полей,
соответствующий элиминации кванторов в 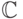 ; к вещественному
случаю мы вернемся.
; к вещественному
случаю мы вернемся.
Поле называется алгебраически замкнутым,
если всякий многочлен, отличный от константы, имеет в нем хотя бы один
корень. (Отсюда легко следует, что любой многочлен разлагается
на линейные множители.) Характеристикой поля называют
минимальное число слагаемых в сумме вида 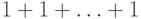 , при
котором она обращается в нуль. Если никакая сумма такого вида не
равна нулю, то поле называют полем характеристики
, при
котором она обращается в нуль. Если никакая сумма такого вида не
равна нулю, то поле называют полем характеристики  .
.
В алгебраически замкнутых полях характеристики  справедливы все обычные свойства многочленов с
комплексными коэффициентами. В частности, корень является
кратным тогда и только тогда, когда он будет корнем производной,
сумма корней с учетом кратности равна степени многочлена и т. д.
Это позволяет заметить, что все преобразования, которые
выполнялись при элиминации кванторов, являются эквивалентными в
произвольных алгебраически замкнутых полях характеристики
справедливы все обычные свойства многочленов с
комплексными коэффициентами. В частности, корень является
кратным тогда и только тогда, когда он будет корнем производной,
сумма корней с учетом кратности равна степени многочлена и т. д.
Это позволяет заметить, что все преобразования, которые
выполнялись при элиминации кванторов, являются эквивалентными в
произвольных алгебраически замкнутых полях характеристики  .
Тем самым мы получаем такую теорему:
.
Тем самым мы получаем такую теорему:
Теорема 38 (о полноте теории алгебраически замкнутых полей
характеристики нуль) Любые два алгебраически замкнутых поля характеристики  элементарно эквивалентны.
элементарно эквивалентны.
(Название этой теоремы станет понятным, когда мы будем говорить о полных теориях.)
81. Покажите, что любые два алгебраически замкнутых поля одной и той же конечной характеристики элементарно эквивалентны.
Теорему 38 можно несколько усилить. Для этого нам понадобится понятие "элементарного расширения".
Пусть фиксирована сигнатура  и две интерпретации этой
сигнатуры с носителями
и две интерпретации этой
сигнатуры с носителями  и
и  . Пусть при этом
. Пусть при этом 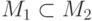 и интерпретации предикатных и функциональных
символов в
и интерпретации предикатных и функциональных
символов в  и
и  согласованы, то есть на
аргументах из
согласованы, то есть на
аргументах из  символы интерпретируются одинаково. (Заметим, что отсюда
следует замкнутость
символы интерпретируются одинаково. (Заметим, что отсюда
следует замкнутость  относительно сигнатурных операций.) В
этом случае
относительно сигнатурных операций.) В
этом случае  иногда называют подструктурой
в
иногда называют подструктурой
в  , а
, а  — расширением
— расширением  .
.
Например, если мы рассматриваем группы как интерпретации
сигнатуры  , то
подструктуры — это подгруппы.
, то
подструктуры — это подгруппы.
82. Почему здесь важно, что операция обращения включена в сигнатуру?
Интерпретацию  называют элементарным расширением
ее подструктуры
называют элементарным расширением
ее подструктуры  , если выполнено такое свойство: для всякой
(не обязательно замкнутой формулы)
, если выполнено такое свойство: для всякой
(не обязательно замкнутой формулы)  и для всякой оценки
и для всякой оценки  со значениями в
со значениями в  формула
формула  истинна в
истинна в  на этой оценке тогда и только тогда, когда она истинна в
на этой оценке тогда и только тогда, когда она истинна в  на той же
оценке.
на той же
оценке.
В частности, если формула замкнута (не содержит параметров), то
ее истинность не зависит от оценки и мы получаем, что  и
и  элементарно эквивалентны.
элементарно эквивалентны.
83. Пусть сигнатура содержит константы для всех элементов
интерпретации  , которая является подструктурой
интерпретации
, которая является подструктурой
интерпретации  . Покажите, что если
интерпретации
. Покажите, что если
интерпретации  и
и  элементарно эквивалентны, то
элементарно эквивалентны, то  является
элементарным расширением
является
элементарным расширением  .
.
Нам понадобится такой пример: пусть имеется поле 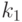 и его
расширение
и его
расширение  . Мы будем рассматривать поля
. Мы будем рассматривать поля 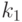 и
и  как две интерпретации сигнатуры
как две интерпретации сигнатуры 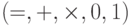 . Пусть имеется
некоторая система полиномиальных уравнений с несколькими
переменными с коэффициентами из
. Пусть имеется
некоторая система полиномиальных уравнений с несколькими
переменными с коэффициентами из 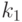 . Тогда утверждение о том,
что она имеет решение, записывается в виде формулы (содержащей
кванторы существования по переменным и конъюнкцию уравнений;
коэффициенты многочленов являются параметрами этой формулы).
Поэтому если
. Тогда утверждение о том,
что она имеет решение, записывается в виде формулы (содержащей
кванторы существования по переменным и конъюнкцию уравнений;
коэффициенты многочленов являются параметрами этой формулы).
Поэтому если  является элементарным расширением
является элементарным расширением 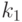 , то всякая система уравнений с коэффициентами в
, то всякая система уравнений с коэффициентами в 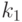 , имеющая
решение в
, имеющая
решение в  , имеет решение и в
, имеет решение и в 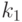 .
.
Теорема 39. Пусть 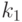 — подполе поля
— подполе поля  , причем оба они
алгебраически замкнуты и имеют характеристику
, причем оба они
алгебраически замкнуты и имеют характеристику  . Тогда
. Тогда  (как интерпретация указанной сигнатуры) является элементарным
расширением интерпретации
(как интерпретация указанной сигнатуры) является элементарным
расширением интерпретации 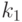 .
.
В самом деле, элиминация кванторов преобразует любую формулу (с
параметрами или без) в эквивалентную ей бескванторную, причем
эквивалентность имеет место в обоих полях. А для бескванторной
формулы ее истинность при оценке со значениями в 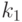 никак не
может зависеть от того, внутри какого поля эта истинность вычисляется.
никак не
может зависеть от того, внутри какого поля эта истинность вычисляется.
Эту теорему называют теоремой о модельной полноте теории алгебраически замкнутых полей характеристики нуль. Из нее с учетом замечания перед ее формулировкой вытекает такой хорошо известный алгебраистам факт:
Теорема 40 (Гильберта о нулях). Всякая система полиномиальных уравнений с коэффициентами в алгебраически замкнутом поле характеристики нуль, имеющая решение в некотором расширении этого поля, имеет решение и в самом поле.
В самом деле, расширение можно еще расширить до алгебраически замкнутого (при этом решение не пропадет), а затем воспользоваться теоремой 39.
84. Другой вариант теоремы Гильберта о нулях формулируется так: пусть дана система уравнений
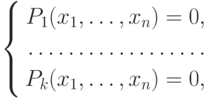
 — многочлены с комплексными коэффициентами,
причем эта система не имеет решения в
— многочлены с комплексными коэффициентами,
причем эта система не имеет решения в 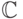 . Тогда можно
найти такие многочлены
. Тогда можно
найти такие многочлены 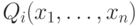 , что
, что
Выведите это утверждение из доказанного нами варианта теоремы
Гильберта о нулях. (Указание: рассмотрим в кольце ![\bbC[x_1,\dots,x_n]](/sites/default/files/tex_cache/773f1f2c163e6e7af8773323fe232b80.png) идеал, порожденный многочленами
идеал, порожденный многочленами 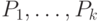 ; если он содержит
единицу, то все доказано, если нет, то расширим его до максимального
идеала
; если он содержит
единицу, то все доказано, если нет, то расширим его до максимального
идеала  ; тогда факторкольцо
; тогда факторкольцо ![\mathbb C[x_1,\dots,x_n]/I](/sites/default/files/tex_cache/96f29fd730f38bdfcdc7dcbbbda84b0a.png) будет полем, расширяющим
будет полем, расширяющим 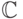 , и в этом поле классы многочленов
, и в этом поле классы многочленов 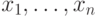 составляют решение нашей системы.)
составляют решение нашей системы.)
