| Россия, Новосибирск |
Арифметика Пресбургера
Элементарная эквивалентность
Пока что мы в основном использовали технику элиминации кванторов для какой-то одной интерпретации (формула заменялась на бескванторную, которая эквивалентна исходной в данной интерпретации). Однако, этот метод позволяет сравнивать различные интерпретации. Мы приведем несколько примеров такого рода.
Начнем с определения. Пусть фиксирована некоторая сигнатура  . Две интерпретации этой сигнатуры называются
элементарно эквивалентными, если в них истинны одни и те
же замкнутые формулы этой сигнатуры.
. Две интерпретации этой сигнатуры называются
элементарно эквивалентными, если в них истинны одни и те
же замкнутые формулы этой сигнатуры.
Легко доказать, что изоморфные интерпретации будут элементарно эквивалентны — надо только дать формальное определение изоморфизма для двух интерпретаций данной сигнатуры.
Пусть  и
и  — две интерпретации сигнатуры
— две интерпретации сигнатуры  . Биекция (взаимно однозначное отображение)
. Биекция (взаимно однозначное отображение) 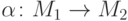 называется изоморфизмом этих интерпретаций, если она
сохраняет все функции и предикаты сигнатуры. Это означает,
что если
называется изоморфизмом этих интерпретаций, если она
сохраняет все функции и предикаты сигнатуры. Это означает,
что если  и
и  — два
— два  -местных
предиката в
-местных
предиката в  и
и  , соответствующих одному предикатному символу
сигнатуры, то
, соответствующих одному предикатному символу
сигнатуры, то
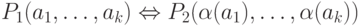
 . Аналогичное условие
для функций: если
. Аналогичное условие
для функций: если  -местные функции
-местные функции 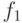 и
и  соответствуют одному функциональному
символу, то
соответствуют одному функциональному
символу, то
 .
.Две интерпретации называются изоморфными, если между ними существует изоморфизм.
Легко понять, что это определение обобщает обычные определения изоморфизма для групп, колец, упорядоченных множеств и т. д.
73. Докажите, что тождественное отображение есть изоморфизм. Докажите, что отображение, обратное изоморфизму, есть изоморфизм. Докажите, что композиция двух изоморфизмов есть изоморфизм. (Отсюда следует, что отношение изоморфности есть отношение эквивалентности на интерпретациях данной сигнатуры.)
Теперь можно сформулировать и доказать обещанное утверждение:
Теорема 35. Изоморфные интерпретации элементарно эквивалентны.
Естественно доказывать это утверждение по индукции. Для этого
его надо обобщить на произвольные формулы (не только замкнутые).
Вот это обобщение: пусть  — изоморфизм,
а
— изоморфизм,
а  — произвольная формула нашей сигнатуры. Тогда она истинна
в
— произвольная формула нашей сигнатуры. Тогда она истинна
в  при оценке
при оценке  тогда и только тогда, когда она
истинна в
тогда и только тогда, когда она
истинна в  при оценке
при оценке  .
.
Обычно истинность формулы  в интерпретации
в интерпретации  обозначают как
обозначают как 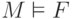 . Если формула имеет параметры
. Если формула имеет параметры 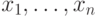 , ее
часто обозначают
, ее
часто обозначают 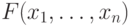 ; при этом запись
; при этом запись 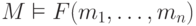 (где
(где 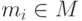 ) означает, что формула
) означает, что формула  истинна при оценке, которая ставит в соответствие параметру
истинна при оценке, которая ставит в соответствие параметру  значение
значение  . После всех этих приготовлений
доказываемое по индукции утверждение можно записать так:
. После всех этих приготовлений
доказываемое по индукции утверждение можно записать так:
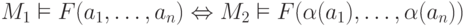
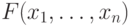 и для любых элементов
и для любых элементов 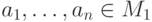 .
.После такого обобщения доказательство по индукции становится очевидным.
74. В каком месте индуктивного рассуждения существенно, что  — взаимно однозначное соответствие? (Ответ:
сюръективность
— взаимно однозначное соответствие? (Ответ:
сюръективность  используется, когда мы рассматриваем
формулу, начинающуюся с квантора существования, и из ее
истинности в
используется, когда мы рассматриваем
формулу, начинающуюся с квантора существования, и из ее
истинности в  выводим истинность в
выводим истинность в  .
Инъективность
.
Инъективность  не используется, но она автоматически
следует из определения изоморфизма, если сигнатура содержит равенство и
интерпретации нормальны, то есть равенство интерпретируется как совпадение элементов.)
не используется, но она автоматически
следует из определения изоморфизма, если сигнатура содержит равенство и
интерпретации нормальны, то есть равенство интерпретируется как совпадение элементов.)
75. Рассуждение, использованное при доказательстве теоремы 35, нам по существу уже встречалось. Где?
Изоморфные интерпретации — это по существу одна и та же интерпретация, только ее элементы названы по-разному. Интересны скорее примеры, когда интерпретации не изоморфны, но тем не менее элементарно эквивалентны. Один такой пример мы уже коротко обсуждали раньше, сформулируем его более подробно.
Теорема 36. Естественные интерпретации сигнатуры  в
множестве рациональных и действительных чисел элементарно эквивалентны.
в
множестве рациональных и действительных чисел элементарно эквивалентны.
Для начала заметим, что эти интерпретации не изоморфны
(поскольку мощности различны). Однако формулы этой сигнатуры
допускают, как мы видели , элиминацию кванторов.При этом получающаяся формула будет эквивалентна исходной
в обеих интерпретациях. Начав с замкнутой формулы,
мы получим бескванторную формулу без переменных (или с
фиктивными переменными, от значений которых ничего не зависит,
тогда вместо них можно подставить, скажем, нули). Эта формула
будет содержать только рациональные константы и потому будет
одинаково истинной в  и в
и в  .
.
Заметим, что при уменьшении сигнатуры элементарная
эквивалентность сохраняется (по очевидным причинам), так что из
теоремы 36 очевидно следует, что  и
и  элементарно эквивалентны как упорядоченные множества
(этот факт мы отмечали).
элементарно эквивалентны как упорядоченные множества
(этот факт мы отмечали).
В этом примере элементарно эквивалентные, но не изоморфные структуры имеют различную мощность. В следующем примере это уже не так.

