| Россия, Новосибирск |
Арифметика Пресбургера
Лемма 2. Пусть  — конечное множество многочленов из
— конечное множество многочленов из ![(\mathbb Z[x_1,\dots,x_n])[x]](/sites/default/files/tex_cache/e4fce03bc9d22fa974664510e9e65884.png) , замкнутое относительно перечисленных
операций. Пусть
, замкнутое относительно перечисленных
операций. Пусть 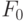 — его часть, состоящая только из многочленов
степени
— его часть, состоящая только из многочленов
степени  по
по  (они представляют собой многочлены
из
(они представляют собой многочлены
из ![\mathbb Z[x_1,\dots,x_n]](/sites/default/files/tex_cache/c757a56015586cc29fdc19aa7dd59dee.png) ). Тогда диаграмма множества
). Тогда диаграмма множества  при данных
при данных 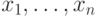 полностью определяется диаграммой
множества
полностью определяется диаграммой
множества 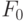 при тех же
при тех же 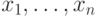 .
.
Заметим, что диаграмма множества 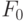 имеет всего один столбец,
указывающий, какие из многочленов положительны, какие
отрицательны и какие равны нулю при данных
имеет всего один столбец,
указывающий, какие из многочленов положительны, какие
отрицательны и какие равны нулю при данных 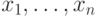 .
Поэтому различным вариантам диаграммы для множества
.
Поэтому различным вариантам диаграммы для множества 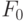 соответствуют полуалгебраические подмножества в
соответствуют полуалгебраические подмножества в 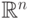 ,
и из леммы 2 следует, что те же самые множества составят искомое
разбиение для полной системы
,
и из леммы 2 следует, что те же самые множества составят искомое
разбиение для полной системы  . Таким образом, нам осталось
лишь доказать лемму 2.
. Таким образом, нам осталось
лишь доказать лемму 2.
Будем добавлять в множество 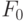 многочлены по одному, в
порядке возрастания (неубывания) их степеней, пока не получим все множество
многочлены по одному, в
порядке возрастания (неубывания) их степеней, пока не получим все множество  . Достаточно показать, что на каждом шаге диаграмма
расширенного множества (с новым многочленом) может быть
однозначно восстановлена по диаграмме предыдущего множества. Мы
сейчас опишем, как это делается.
. Достаточно показать, что на каждом шаге диаграмма
расширенного множества (с новым многочленом) может быть
однозначно восстановлена по диаграмме предыдущего множества. Мы
сейчас опишем, как это делается.
Пусть добавляется многочлен ![P\hm\in(\mathbb Z[x_1,\dots,x_n])[x]](/sites/default/files/tex_cache/2ff7a9602983c9e558a460362e8c1293.png) ,
при этом многочлены всех меньших степеней из
,
при этом многочлены всех меньших степеней из  уже есть в
диаграмме. В силу замкнутости
уже есть в
диаграмме. В силу замкнутости  старший коэффициент многочлена
старший коэффициент многочлена  содержится в
содержится в  и, имея меньшую (нулевую)
степень, уже представлен в диаграмме. (Соответствующая строка состоит из одинаковых знаков,
так как он не зависит от
и, имея меньшую (нулевую)
степень, уже представлен в диаграмме. (Соответствующая строка состоит из одинаковых знаков,
так как он не зависит от  .) Если там стоят нули, то (при
данных
.) Если там стоят нули, то (при
данных 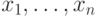 ) старший коэффициент равен нулю, и
многочлен
) старший коэффициент равен нулю, и
многочлен  совпадает с многочленом, получающимся при
отбрасывании старшего члена. Этот многочлен тоже есть в
совпадает с многочленом, получающимся при
отбрасывании старшего члена. Этот многочлен тоже есть в  и в
диаграмме, так что надо лишь продублировать соответствующую строку.
и в
диаграмме, так что надо лишь продублировать соответствующую строку.
Итак, достаточно рассмотреть случай, когда старший коэффициент
многочлена  (при данных
(при данных 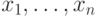 ) не равен
нулю. Пополнение диаграммы включает в себя два шага: сначала мы должны
определить знаки многочлена
) не равен
нулю. Пополнение диаграммы включает в себя два шага: сначала мы должны
определить знаки многочлена  в точках (корнях), уже входящих в
диаграмму. Затем надо пополнить диаграмму корнями многочлена
в точках (корнях), уже входящих в
диаграмму. Затем надо пополнить диаграмму корнями многочлена  (при этом число столбцов в ней увеличится).
(при этом число столбцов в ней увеличится).
Как найти знак многочлена  в одной из старых точек? По
определению диаграммы в этой точке (обозначим ее
в одной из старых точек? По
определению диаграммы в этой точке (обозначим ее  ) один
из старых многочленов равен нулю. Пусть
) один
из старых многочленов равен нулю. Пусть  — такой многочлен.
Можно считать, что старший коэффициент
— такой многочлен.
Можно считать, что старший коэффициент 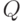 (как многочлена от
(как многочлена от  ) отличен от нуля при данных
) отличен от нуля при данных 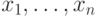 .
Если это не так, заменим
.
Если это не так, заменим 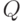 на многочлен,
получающийся отбрасыванием старшего члена. Мы знаем, что
множество
на многочлен,
получающийся отбрасыванием старшего члена. Мы знаем, что
множество  замкнуто относительно четырех операций и что все
многочлены из
замкнуто относительно четырех операций и что все
многочлены из  , имеющие меньшую степень, уже входят в
диаграмму. Поэтому вся необходимая информация для отбора
подходящего
, имеющие меньшую степень, уже входят в
диаграмму. Поэтому вся необходимая информация для отбора
подходящего 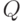 у нас есть.
у нас есть.
Кроме того, по тем же причинам нам известен знак старшего
коэффициента многочлена 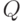 . Применим операцию модифицированного
деления с остатком к
. Применим операцию модифицированного
деления с остатком к  и
и 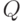 :
:

 — старший коэффициент многочлена
— старший коэффициент многочлена 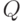 ).
Подставим в это равенство число
).
Подставим в это равенство число  . При этом
. При этом 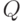 обратится в
нуль, так как
обратится в
нуль, так как  является корнем
является корнем 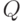 по построению.
Многочлен
по построению.
Многочлен  входит в диаграмму в силу наших предположений, так что его
знак в точке
входит в диаграмму в силу наших предположений, так что его
знак в точке  нам известен, как и знак
нам известен, как и знак  .
Тем самым можно найти знак
.
Тем самым можно найти знак  .
.Итак, мы определили знак нового многочлена в старых корнях.
Покажем, что этого достаточно, чтобы предсказать, на каких
участках диаграммы появятся новые корни (многочлена  ). При
этом нам пригодится (пока что не использованная) операция
дифференцирования.
). При
этом нам пригодится (пока что не использованная) операция
дифференцирования.
Если в двух соседних старых корнях 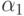 ,
,  многочлен
многочлен  имеет один и тот же знак (скажем,
положителен), то между ними нет нового корня. В самом деле, если
бы на интервале
имеет один и тот же знак (скажем,
положителен), то между ними нет нового корня. В самом деле, если
бы на интервале 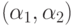 многочлен
многочлен  обращался в нуль, то минимум многочлена
обращался в нуль, то минимум многочлена  на
на ![[\alpha_1,\alpha_2]](/sites/default/files/tex_cache/21edb50d11f04906588bebfaeedf061f.png) достигался бы в некоторой внутренней точке, в которой
производная
достигался бы в некоторой внутренней точке, в которой
производная 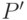 равнялась бы нулю. Но производная
равнялась бы нулю. Но производная 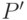 входит в множество
входит в множество  и представлена в диаграмме, так что тогда
и представлена в диаграмме, так что тогда 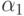 и
и  не были бы соседними корнями
диаграммы.
не были бы соседними корнями
диаграммы.
Если в одной из точек 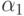 и
и  многочлен
многочлен  обращается в нуль, то на интервале
обращается в нуль, то на интервале 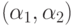 он
корней иметь не может (по теореме Ролля такой корень повлек бы за собой корень производной).
он
корней иметь не может (по теореме Ролля такой корень повлек бы за собой корень производной).
Наконец, если 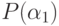 и
и 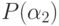 имеют
разные знаки, то по теореме о промежуточном значении многочлен
имеют
разные знаки, то по теореме о промежуточном значении многочлен  имеет на
интервале
имеет на
интервале 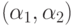 хотя бы один корень. При этом по
уже понятным нам причинам (теорема Ролля) двух корней он иметь
не может. Это позволяет вставить столбец для этого корня в
диаграмму. При этом соответствующий интервал диаграммы
разобьется на два, которые будут отличаться лишь в строке для
многочлена
хотя бы один корень. При этом по
уже понятным нам причинам (теорема Ролля) двух корней он иметь
не может. Это позволяет вставить столбец для этого корня в
диаграмму. При этом соответствующий интервал диаграммы
разобьется на два, которые будут отличаться лишь в строке для
многочлена  .
.
Осталось провести аналогичное рассуждение для лучей, стоящих с
края диаграммы. Поведение многочлена  на бесконечности
определяется его старшим коэффициентом (который, напомним, не
равен нулю — сейчас мы впервые используем это предположение).
Поэтому если
на бесконечности
определяется его старшим коэффициентом (который, напомним, не
равен нулю — сейчас мы впервые используем это предположение).
Поэтому если  стремится, скажем, к
стремится, скажем, к  при
при 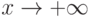 , а значение
, а значение  в самом правом корне было
отрицательным, то на этом луче появляется новый корень (только
один по теореме Ролля). Если же значение
в самом правом корне было
отрицательным, то на этом луче появляется новый корень (только
один по теореме Ролля). Если же значение  в самом правом
корне равно нулю или имеет тот же знак, что и старший
коэффициент, то мы повторяем рассуждение из предыдущего абзаца и
убеждаемся, что корней
в самом правом
корне равно нулю или имеет тот же знак, что и старший
коэффициент, то мы повторяем рассуждение из предыдущего абзаца и
убеждаемся, что корней  на правом луче нет. Аналогично
определяется и поведение
на правом луче нет. Аналогично
определяется и поведение  слева от самого левого корня.
слева от самого левого корня.
На этом доказательство леммы 2, а с ней и теоремы Тарского-Зайденбрега, завершается.
67. Докажите, что множество троек 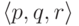 ,
при которых многочлен
,
при которых многочлен 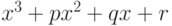 имеет ровно два
положительных корня, является полуалгебраическим.
имеет ровно два
положительных корня, является полуалгебраическим.
Подобного рода задачи рассматривались в алгебре еще в прошлом веке (число перемен знака, правило Штурма и др.).
68. Докажите, что предикат 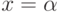 , где
, где  —
некоторое действительное число, выразим тогда и только тогда,
когда
—
некоторое действительное число, выразим тогда и только тогда,
когда  является алгебраическим.
является алгебраическим.
Разобравшись с действительными числами, можно перейти к комплексным. На самом деле (как часто бывает) здесь ситуация проще.
На комплексных числах нет естественного отношения порядка, поэтому
рассмотрим сигнатуру 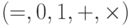 . Будем, как
всегда, считать две формулы эквивалентными, если
они истинны при одних и тех же значениях параметров (в
естественной интерпретации с носителем
. Будем, как
всегда, считать две формулы эквивалентными, если
они истинны при одних и тех же значениях параметров (в
естественной интерпретации с носителем 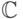 ).
).
Теорема 34 (элиминация кванторов в поле комплексных чисел). Всякая формула этой сигнатуры эквивалентна бескванторной.
Эта теорема имеет много разных доказательств, но после доказательства теоремы Тарского-Зайденберга нам проще всего модифицировать его.
Теперь в диаграммах будут стоять не знаки 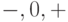 , а только
знаки
, а только
знаки  и
и 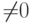 (поскольку порядка
на
(поскольку порядка
на 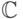 нет). По той же
причине мы не можем упорядочить корни, так что диаграмма будет
состоять из неупорядоченных столбцов, соответствующих корням, и
одного столбца, соответствующего дополнению к множеству корней
(в котором будут стоять знаки
нет). По той же
причине мы не можем упорядочить корни, так что диаграмма будет
состоять из неупорядоченных столбцов, соответствующих корням, и
одного столбца, соответствующего дополнению к множеству корней
(в котором будут стоять знаки 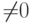 для всех многочленов,
кроме нулевых). Говоря о неупорядоченных столбцах, мы имеем в
виду, что не различаем диаграммы, отличающиеся лишь порядком
столбцов.
для всех многочленов,
кроме нулевых). Говоря о неупорядоченных столбцах, мы имеем в
виду, что не различаем диаграммы, отличающиеся лишь порядком
столбцов.
Основной шаг в доказательстве теоремы Тарского-Зайденберга (единственный, где важен порядок на действительных числах) состоял в пополнении диаграммы новым многочленом. Что будет с ним теперь?
Как и раньше, мы можем определить, в каких старых корнях новый
многочлен равен нулю. Более того, мы можем определить кратность
этих нулей, так как знаем все необходимое про его производные
(которые уже включены в диаграмму). Поэтому основная теорема
алгебры говорит нам, сколько будет новых корней (заметим, что все
новые корни имеют кратность  , так как иначе они были бы
корнями производной и не были бы новыми). Поскольку порядка
на корнях нет, больше никакой информации нам и не нужно.
, так как иначе они были бы
корнями производной и не были бы новыми). Поскольку порядка
на корнях нет, больше никакой информации нам и не нужно.
69. Провести доказательство элиминации кванторов в поле 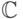 , не
использующее диаграмм (это можно сделать, начав с приведения
бескванторной формулы к дизъюнктивной нормальной форме, а затем
применяя разные соображения из алгебры о наибольшем общем
делителе многочленов). Для теоремы Тарского-Зайденберга это
несколько сложнее; рассуждение такого рода приведено в книжке
Энгелера [32]
, не
использующее диаграмм (это можно сделать, начав с приведения
бескванторной формулы к дизъюнктивной нормальной форме, а затем
применяя разные соображения из алгебры о наибольшем общем
делителе многочленов). Для теоремы Тарского-Зайденберга это
несколько сложнее; рассуждение такого рода приведено в книжке
Энгелера [32]
70. Докажите, что множество тех четверок комплексных чисел 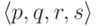 , при которых многочлены
, при которых многочлены 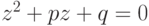 и
и 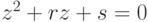 имеют общий корень, задается бескванторной формулой.
Найти эту формулу.
имеют общий корень, задается бескванторной формулой.
Найти эту формулу.
Задача 70 хорошо знакома алгебраистам. Ответ в ней можно
записать в виде 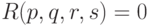 , где
, где  — многочлен,
называемый результантом и равный определителю матрицы
— многочлен,
называемый результантом и равный определителю матрицы
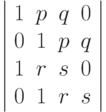
71. Докажите, что множество всех пар комплексных чисел  , при которых многочлен
, при которых многочлен  имеет хотя бы
один кратный корень, задается бескванторной формулой. Найти эту
формулу. Как выглядит аналогичная формула для многочлена
имеет хотя бы
один кратный корень, задается бескванторной формулой. Найти эту
формулу. Как выглядит аналогичная формула для многочлена  ?
?
(Ответ к задаче тоже хорошо известен в алгебре; соответствующий многочлен называется дискриминантом.)
72. Обобщить утверждение предыдущей задачи на многочлены
произвольной степени со старшим коэффициентом  и найти
выражение дискриминанта в виде определителя.
и найти
выражение дискриминанта в виде определителя.
