Диаграммы

Неполные и неразрешимые теории

Предыдущий раздел мог создать впечатление, что наугад взятая теория скорее всего окажется полной, разрешимой, а возможно, и конечно аксиоматизируемой. Это совсем не так.

Откуда вообще берутся в математике аксиоматические теории? Иногда мы пытаемся построить аксиоматически теорию какой-то конкретной структуры (скажем, теорию действительных чисел со сложением и умножением). В других случаях мы стараемся выделить общие свойства различных структур. Например, аксиомы группы фиксируют общие свойства различных групп, и с самого начала ясно, что такая теория не должна и не может быть полной. То же самое можно сказать и про теорию линейно упорядоченных множеств — полнота такой теории означала бы, что все линейно упорядоченные множества (или группы) элементарно эквивалентны, то есть обладают одними и теми же свойствами, выражаемыми формулами. Это, конечно, не так.

Что касается конкретных структур, то и для них естественные теории не всегда оказываются полными. Классический пример — натуральные числа со сложением и умножением. Для них имеется естественная формальная теория (называемая формальной арифметикой). Ее аксиомы включают в себя обычные свойства сложения и умножения, а также аксиомы индукции. Опыт показывает, что любое рассуждение теории чисел, в котором речь идет только о конечных объектах, может быть формально записано в виде вывода из аксиом этой теории. Более того, многие доказательства, использующие бесконечные объекты (скажем, важнейшую в теории чисел -функцию Римана), могут быть модифицированы и погружены в эту формальную теорию. Тем не менее эта теория неполна (и не может быть полна, как мы увидим в этом разделе).

Среди естественных неполных теорий бывают разрешимые и неразрешимые. Например, теория линейно упорядоченных множеств разрешима, теория абелевых групп разрешима, а теория групп неразрешима. Подробный рассказ об этом далеко выходит за рамки нашей книжки; написанный М.О.Рабином обзор соответствующих результатов можно найти в справочнике по математической логике (часть III, Теория рекурсии [26], глава 4).

Мы же ограничимся тремя примерами (теория равенства, теория полугрупп, формальная арифметика).

Теория равенства

Рассмотрим сигнатуру, содержащую единственный двуместный предикат равенства, и теорию, состоящую из трех аксиом равенства (рефлексивность, симметричность и транзитивность). Эти аксиомы рассматривались в разделе "Аксиомы равенства"; заметим, что у нас нет других предикатных и функциональных символов (и связанных с ними аксиом равенства).

Моделями этой теории являются всевозможные множества с отношениями эквивалентности. Нормальными моделями этой теории являются множества различной мощности; поскольку никакой дополнительной структуры нет, такая модель определяется мощностью (с точностью до изоморфизма). Теоремами этой теории будут формулы с равенством, истинные в множествах любой мощности.

Теорема 68.Множество теорем теории равенства является разрешимым.

Заметим, что истинность формулы в нормальной модели может зависеть от ее мощности. Например, формула ложна в одноэлементной модели и истинна во всех остальных. Поэтому процедура элиминации кванторов в чистом виде здесь неприменима.

Но идея остается той же. От чего зависит истинность формулы этой сигнатуры (с параметрами)? Во-первых, от значений параметров (важно, какие параметры равны друг другу, а какие нет). Во-вторых, от числа элементов модели. (Если бы этой зависимости не было, то можно было бы написать бескванторную формулу, эквивалентную данной во всех моделях теории.)

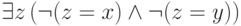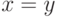Например, формула при истинна во всех моделях, начиная с двухэлементной, а при истинна во всех моделях, начиная с трехэлементной. Можно ожидать, что модели с большим числом элементов неотличимы друг от друга и от бесконечных моделей.

Лемма. Истинность формулы языка с равенством, содержащей параметров и имеющей кванторную глубину , определяется тем, какие из параметров равны друг другу, а также мощностью носителя, при этом все мощности, большие , одинаковы.

Доказательство леммы проводится индукцией по построению формулы. Для атомарной (и вообще для любой бескванторной) формулы мощность вообще не играет роли. Если утверждение леммы верно для формул и , то оно очевидным образом верно и для 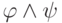, , и 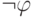. При этом используется такой факт: кванторная глубина (число вложенных кванторов) и число параметров у части формулы не больше, чем у всей формулы.

Содержательный случай — когда формула начинается с квантора. Когда, скажем, формула

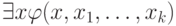
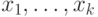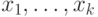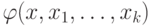с параметрами будет истинной (в данной интерпретации при данных значениях параметров)? Достаточно попробовать в качестве значения а также какой-нибудь элемент, отличный от всех этих значений. (Все такие элементы ничем не отличаются.) Истинность формулы при 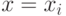определяется соотношениями между параметрами и мощностью модели (по предположению индукции; заметим, что число параметров увеличилось на , а кванторная глубина уменьшилась на , так что сумма осталась прежней). Существование элемента, отличного от всех , определяется мощностью модели и числом различных элементов среди 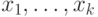(то есть в конечном счете равенствами вида ). При этом модели всех мощностей, начиная с , ведут себя одинаково. 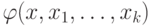Кроме того, истинность формулы при 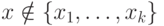по предположению индукции также определяется равенствами вида и мощностью модели.

Квантор всеобщности рассматривается точно так же (а можно его выразить через квантор существования и вообще не рассматривать). Лемма доказана.

Доказательство леммы конструктивно, то есть указывает способ узнать, будет ли формула истинной, если известно, какие ее параметры равны и какова мощность носителя. В частности, для замкнутых формул получаем способ проверять их истинность для всех значений мощности, то есть выводимость в теории равенства.

140. Рассмотрим теорию, в сигнатуре которой есть равенство и конечное число одноместных предикатных символов, а аксиомами являются аксиомы равенства (включая устойчивость предикатов относительно равенства, как в разделе "Аксиомы равенства"). Покажите, что эта теория разрешима.

Эта задача показывает, что добавление одноместных предикатов в сигнатуру не делает теорию равенства неразрешимой. Отметим, что расширение сигнатуры (без изменения множества аксиом) может превратить разрешимую теорию в неразрешимую: например, добавив конечное число одноместных функциональных символов к теории равенства, получим неразрешимую теорию (как видно из доказательства теоремы Черча с помощью проблемы тождества для полугрупп, см. [5]). Добавление одного двуместного предикатного символа также дает неразрешимую теорию.